Con el módulo desigualdades trigonométricas. Curso: Ecuaciones y desigualdades trigonométricas

- π - arcosen a + 2πn< t < arcsin a + 2πn, nєZ.

¡Aplícalo a los ejemplos considerados y obtendrás una respuesta mucho más rápido!

Conclusión: ¡APRENDAN LA FÓRMULA, AMIGOS!

Página 1 de 1 1

Un algoritmo para resolver las desigualdades trigonométricas más simples y reconocer formas de resolver desigualdades trigonométricas.

Docentes de la máxima categoría de cualificación:

Shirko FM Pueblo de progreso, MOBU-SOSH №6

Sankina L. S. Armavir, PEI Secundaria "Nuevo Camino"

No existen métodos universales de enseñanza de las disciplinas matemático-naturales. Cada maestro encuentra sus propias formas de enseñar aceptables solo para él.

Nuestros muchos años de experiencia docente muestran que los estudiantes aprenden más fácilmente material que requiere concentración de atención y almacenamiento de una gran cantidad de información en la memoria si se les enseña a usar algoritmos en sus actividades en la etapa inicial de aprendizaje de un tema complejo. Tal tema, en nuestra opinión, es el tema de resolver desigualdades trigonométricas.

Entonces, antes de comenzar con los estudiantes a identificar técnicas y métodos para resolver desigualdades trigonométricas, elaboramos y arreglamos el algoritmo para resolver las desigualdades trigonométricas más simples.

Algoritmo para resolver las desigualdades trigonométricas más simples

Marcamos puntos en el eje correspondiente ( por pecado X- eje y, paraporque X- Eje BUEY)

Restauramos la perpendicular al eje, que cortará el círculo en dos puntos.

Primero sobre la circunferencia firmamos el punto que pertenece al intervalo del rango de valores de la función arco por definición.

Partiendo del punto firmado, sombreamos el arco de un círculo correspondiente a la parte sombreada del eje.

Prestamos especial atención a la dirección de la circunvalación. Si el recorrido es en el sentido de las agujas del reloj (es decir, hay una transición a través de 0), entonces el segundo punto en el círculo será negativo, si es en el sentido contrario a las agujas del reloj, positivo.

Escribimos la respuesta como un intervalo, teniendo en cuenta la periodicidad de la función.

Consideremos el funcionamiento del algoritmo con ejemplos.

1) pecado ≥ 1/2;

Solución:

Dibuja un círculo unitario.;

Marcamos un punto ½ en el eje y.

Restaurar la perpendicular al eje,

que corta a la circunferencia en dos puntos.

Por la definición del arcoseno, marcamos primero

punto π/6.

Sombreamos la parte del eje que corresponde a

dada la desigualdad, por encima del punto ½.

Sombreamos el arco de un círculo correspondiente a la parte sombreada del eje.

El bypass se realiza en sentido antihorario, obtuvimos el punto 5π/6.

Escribimos la respuesta como un intervalo, teniendo en cuenta la periodicidad de la función;

Responder:X;[π/6 + 2π norte, 5π/6 + 2π norte], norte z

La desigualdad más simple se resuelve usando el mismo algoritmo si no hay un valor tabular en el registro de respuesta.

Los estudiantes, en las primeras lecciones, resolviendo desigualdades en la pizarra, pronuncian en voz alta cada paso del algoritmo.

2) 5 porque X – 1 ≥ 0;

R Solución:a

5 porque X – 1 ≥ 0;

porque X ≥ 1/5;

Dibuja un círculo unitario.

Marcamos en el eje OX un punto de coordenada 1/5.

Restauramos la perpendicular al eje, que

corta a la circunferencia en dos puntos.

Primero sobre la circunferencia firmamos el punto que pertenece al intervalo del rango de valores del arcocoseno por definición (0; π).

Sombreamos la parte del eje que corresponde a esta desigualdad.

A partir del punto firmado arccos 1/5, sombrea el arco de un círculo correspondiente a la parte sombreada del eje.

El bypass se realiza en el sentido de las agujas del reloj (es decir, hay una transición a través de 0), lo que significa que el segundo punto del círculo será negativo: arccos 1/5.

Escribimos la respuesta como un intervalo, teniendo en cuenta la periodicidad de la función, de menor valor a mayor.

Responder: X  [-arccos 1/5 + 2π norte, arccos 1/5 + 2π norte], norte z

La mejora de la capacidad para resolver desigualdades trigonométricas se ve facilitada por las preguntas: "¿Cómo resolveremos un grupo de desigualdades?"; “¿En qué se diferencia una desigualdad de otra?”; “¿En qué se parece una desigualdad a otra?”; ¿Cómo cambiaría la respuesta si se diera una desigualdad estricta? ¿Cómo cambiaría la respuesta si hubiera un signo en lugar del signo ""

La tarea de analizar la lista de desigualdades desde el punto de vista de las formas de resolverlas le permite resolver su reconocimiento.

A los estudiantes se les dan desigualdades para resolver en clase.

Pregunta: Resalta las desigualdades que requieren el uso de transformaciones equivalentes al reducir la desigualdad trigonométrica a la más simple?

Responder 1, 3, 5.

Pregunta:¿Cuáles son las desigualdades en las que se requiere considerar un argumento complejo como uno simple?

Responder: 1, 2, 3, 5, 6.

Pregunta:¿Cuáles son las desigualdades donde se pueden aplicar fórmulas trigonométricas?

Responder: 2, 3, 6.

Pregunta:¿Cuáles son las desigualdades donde se puede aplicar el método de introducir una nueva variable?

Responder: 6.

La tarea de analizar la lista de desigualdades desde el punto de vista de las formas de resolverlas le permite resolver su reconocimiento. Al desarrollar habilidades, es importante señalar las etapas de su implementación y formularlas en forma general, que se presenta en el algoritmo para resolver las desigualdades trigonométricas más simples.

MÉTODOS PARA RESOLVER DESIGUALDADES TRIGONOMÉTRICAS

Relevancia. Históricamente, a las ecuaciones y desigualdades trigonométricas se les ha dado un lugar especial en el currículo escolar. Podemos decir que la trigonometría es una de las secciones más importantes del curso escolar y de todas las ciencias matemáticas en general.

Las ecuaciones y desigualdades trigonométricas ocupan uno de los lugares centrales en un curso de matemáticas de secundaria, tanto en términos del contenido del material educativo como de los métodos de actividad educativa y cognitiva que pueden y deben formarse durante su estudio y aplicarse para resolver un gran número de problemas. serie de problemas de carácter teórico y aplicado.

La solución de ecuaciones y desigualdades trigonométricas crea los requisitos previos para sistematizar el conocimiento de los estudiantes relacionado con todo el material educativo en trigonometría (por ejemplo, las propiedades de las funciones trigonométricas, métodos para transformar expresiones trigonométricas, etc.) y permite establecer conexiones efectivas con el material estudiado en álgebra (ecuaciones, equivalencia de ecuaciones, desigualdades, transformaciones idénticas de expresiones algebraicas, etc.).

En otras palabras, la consideración de métodos para resolver ecuaciones y desigualdades trigonométricas implica una especie de transferencia de estas habilidades a un nuevo contenido.

La trascendencia de la teoría y sus numerosas aplicaciones son prueba de la relevancia del tema elegido. Esto, a su vez, le permite determinar las metas, los objetivos y el tema de investigación del trabajo de curso.

Propósito del estudio: generalizar los tipos disponibles de desigualdades trigonométricas, métodos básicos y especiales para su solución, seleccionar un conjunto de tareas para resolver desigualdades trigonométricas por escolares.

Investigar objetivos:

1. A partir del análisis de la literatura disponible sobre el tema de investigación, sistematizar el material.

2. Dar un conjunto de tareas necesarias para consolidar el tema "Desigualdades trigonométricas".

Objeto de estudio son desigualdades trigonométricas en el curso de matemáticas escolares.

Tema de estudio: tipos de desigualdades trigonométricas y métodos para su solución.

Importancia teórica es organizar el material.

Significado práctico: aplicación de conocimientos teóricos en la resolución de problemas; análisis de los principales métodos frecuentemente encontrados para resolver desigualdades trigonométricas.

Métodos de búsqueda : análisis de la literatura científica, síntesis y generalización de los conocimientos adquiridos, análisis de la resolución de problemas, búsqueda de métodos óptimos para la resolución de desigualdades.

§una. Tipos de desigualdades trigonométricas y métodos básicos para su solución

1.1. Las desigualdades trigonométricas más simples.

Dos expresiones trigonométricas conectadas por un signo o > se llaman desigualdades trigonométricas.

Resolver una desigualdad trigonométrica significa encontrar un conjunto de valores de las incógnitas incluidas en la desigualdad, bajo los cuales se satisface la desigualdad.

La parte principal de las desigualdades trigonométricas se resuelve reduciéndolas a resolver las más simples:

Este puede ser un método de factorización, cambio de variable (
,
etc.), donde primero se resuelve la desigualdad habitual y luego la desigualdad de la forma
etc., u otras formas.

Las desigualdades más sencillas se resuelven de dos formas: usando el círculo unitario o gráficamente.

Dejarf(x  es una de las funciones trigonométricas básicas. Para resolver la desigualdad
basta con encontrar su solución en un período, es decir, en cualquier segmento cuya longitud es igual al período de la funciónF  X  . Entonces la solución de la desigualdad original será encontradaX , así como aquellos valores que difieren de los encontrados por cualquier número entero de periodos de la función. En este caso, es conveniente utilizar el método gráfico.

Pongamos un ejemplo de un algoritmo para resolver desigualdades.
(
) y
.

Algoritmo para resolver la desigualdad
(
).

1. Formular la definición del seno de un númeroX en el círculo unitario.

3. En el eje y, marque un punto con la coordenadaa .

4. A través de este punto, dibuje una línea paralela al eje OX y marque los puntos de intersección de la misma con el círculo.

5. Seleccione un arco de círculo, cuyos puntos tengan una ordenada menor quea .

6. Especifique la dirección de la derivación (en sentido contrario a las agujas del reloj) y escriba la respuesta sumando el período de la función a los extremos del intervalo.2πn ,
.

Algoritmo para resolver la desigualdad
.

1. Formular la definición de la tangente de un númeroX en el círculo unitario.

2. Dibuja un círculo unitario.

3. Dibuja una recta de tangentes y marca un punto en ella con una ordenadaa .

4. Conecte este punto al origen y marque el punto de intersección del segmento resultante con el círculo unitario.

5. Seleccione un arco de círculo, cuyos puntos tengan una ordenada en la línea tangente que sea menor quea .

6. Indique la dirección del recorrido y anote la respuesta, teniendo en cuenta el alcance de la función, agregando un puntopn ,
(el número del lado izquierdo del registro siempre es menor que el número del lado derecho).

En el apéndice (Apéndices 1 y 2) se proporciona una interpretación gráfica de las soluciones de las ecuaciones y fórmulas más simples para resolver desigualdades en forma general.

Ejemplo 1 Resuelve la desigualdad
.

Dibujar una línea en el círculo unitario
, que corta a la circunferencia en los puntos A y B.

Todos los valoresy en el intervalo NM más , todos los puntos del arco AMB satisfacen esta desigualdad. En todos los ángulos de rotación, grandes , pero más pequeño ,
tomará valores mayores que (pero no más de uno).

Figura 1

Así, la solución de la desigualdad serán todos los valores en el intervalo
, es decir.
. Para obtener todas las soluciones de esta desigualdad, basta con sumar a los extremos de este intervalo
, dónde
, es decir.
,
. Tenga en cuenta que los valores
y
son las raices de la ecuacion
,

aquellos.
;
.

Responder:
,
.

1.2. Método gráfico

En la práctica, suele ser útil un método gráfico para resolver desigualdades trigonométricas. Considere la esencia del método en el ejemplo de la desigualdad.
:

1. Si el argumento es complejo (diferente deX ), luego lo reemplazamos cont .

2. Construimos en un plano de coordenadasjuguete gráficas de funciones
y
.

3. Encontramos taldos puntos adyacentes de intersección de gráficos, entre los cualessinusoidesituadoarriba directo
. Encuentre las abscisas de estos puntos.

4. Escribe una desigualdad doble para el argumentot , considerando el periodo del coseno (t estará entre las abscisas encontradas).

5. Haz una sustitución inversa (vuelve al argumento original) y expresa el valorX a partir de una doble desigualdad, escribimos la respuesta como un intervalo numérico.

Ejemplo 2 Resuelve la desigualdad: .

Al resolver desigualdades por un método gráfico, es necesario construir gráficos de funciones con la mayor precisión posible. Transformemos la desigualdad a la forma:

Construyamos gráficas de funciones en un sistema de coordenadas
y
(Figura 2).

Figura 2

Los gráficos de funciones se intersecan en un puntoPERO con coordenadas
;
. Entre
puntos del gráfico
debajo de los puntos del gráfico
. Y cuando
los valores de la función son los mismos. Es por eso
a
.

Responder:
.

1.3. Método algebraico

Muy a menudo, la desigualdad trigonométrica original, mediante una sustitución bien elegida, puede reducirse a una desigualdad algebraica (racional o irracional). Este método consiste en transformar la desigualdad, introducir una sustitución o reemplazar una variable.

Consideremos la aplicación de este método en ejemplos concretos.

Ejemplo 3 Reducción a la forma más simple
.

(Fig. 3)

Fig. 3

,
.

Responder:
,

Ejemplo 4 Resuelve la desigualdad:

ODZ:
,
.

Usando fórmulas:
,

escribimos la desigualdad en la forma:
.

O, suponiendo
después de simples transformaciones obtenemos

,

,

.

Resolviendo la última desigualdad por el método del intervalo, obtenemos:

Figura 4

, respectivamente
. Luego de la Fig. 4 sigue
, dónde
.

Figura 5

Responder:
,
.

1.4. Método de espaciado

El esquema general para resolver desigualdades trigonométricas por el método de intervalo:

Usando fórmulas trigonométricas, factoriza.

Encuentre puntos de ruptura y ceros de la función, colóquelos en el círculo.

Toma cualquier puntoA (pero no encontrado antes) y averigüe el signo del producto. Si el producto es positivo, coloque un punto fuera del círculo unitario en el rayo correspondiente al ángulo. De lo contrario, coloque el punto dentro del círculo.

Si un punto aparece un número par de veces, lo llamamos punto de multiplicidad par; si ocurre un número impar de veces, lo llamamos punto de multiplicidad impar. Dibuja arcos de la siguiente manera: comienza desde un puntoA , si el siguiente punto es de multiplicidad impar, entonces el arco interseca al círculo en este punto, pero si el punto es de multiplicidad par, entonces no interseca.

Los arcos detrás de un círculo son espacios positivos; dentro del círculo hay intervalos negativos.

Ejemplo 5 Resuelve la desigualdad

,
.

Puntos de la primera serie:
.

Puntos de la segunda serie:
.

Cada punto ocurre un número impar de veces, es decir, todos los puntos de multiplicidad impar.

Descubra la marca del producto en
: . Marcamos todos los puntos en el círculo unitario (Fig. 6):

Arroz. 6

Responder:
,
;
,
;
,
.

Ejemplo 6 . Resuelve la desigualdad.

Solución:

Encontremos los ceros de la expresión .

Obteneraemetro :

,
;

,
;

,
;

,
;

En el círculo unitario, valores de serieX 1 representado por puntos
. SerieX 2 da puntos
. Una serieX 3 obtenemos dos puntos
. Finalmente, una serieX 4 representará puntos
. Ponemos todos estos puntos en el círculo unitario, indicando entre paréntesis al lado de cada uno su multiplicidad.

Ahora deja el número será igual. Hacemos una estimación por el signo:

entonces el puntoA debe elegirse en la viga que forma el ángulo con vigaVaya, fuera del círculo unitario. (Tenga en cuenta que la viga auxiliarO A no tiene que ser mostrado en la imagen. PuntoA seleccionado aproximadamente.)

Ahora desde el puntoA dibujamos una línea continua ondulada secuencialmente a todos los puntos marcados. y en los puntos
nuestra línea pasa de una región a otra: si estaba fuera del círculo unitario, entonces pasa a él. Acercándose al punto , la línea vuelve a la región interior, ya que la multiplicidad de este punto es par. Del mismo modo en el punto (con una multiplicidad par) la línea debe girarse hacia la región exterior. Entonces, dibujamos una cierta imagen representada en la Fig. 7. Ayuda a resaltar las áreas deseadas en el círculo unitario. Están marcados con un "+".

Figura 7

Respuesta final:

Nota. Si la línea ondulada, después de atravesar todos los puntos marcados en el círculo unitario, no puede regresar al puntoA , sin cruzar el círculo en un lugar “ilegal”, esto significa que se cometió un error en la solución, es decir, se omitió un número impar de raíces.

Responder: .

§2. Un conjunto de tareas para resolver desigualdades trigonométricas.

En el proceso de desarrollo de la capacidad de los escolares para resolver desigualdades trigonométricas, también se pueden distinguir 3 etapas.

1. preparatorio,

2. formación de habilidades para resolver las desigualdades trigonométricas más simples;

3. Introducción de desigualdades trigonométricas de otro tipo.

El propósito de la etapa preparatoria es que es necesario formar en los escolares la habilidad de usar un círculo o gráfico trigonométrico para resolver desigualdades, a saber:

Habilidad para resolver desigualdades simples de la forma
,
,
,
, utilizando las propiedades de las funciones seno y coseno;

Habilidad para hacer desigualdades dobles para arcos de un círculo numérico o para arcos de gráficas de funciones;

Capacidad para realizar diversas transformaciones de expresiones trigonométricas.

Se recomienda implementar esta etapa en el proceso de sistematización de los conocimientos de los escolares sobre las propiedades de las funciones trigonométricas. Los medios principales pueden ser tareas ofrecidas a los estudiantes y realizadas bajo la guía de un maestro o de forma independiente, así como las habilidades adquiridas en la resolución de ecuaciones trigonométricas.

Aquí hay ejemplos de tales tareas:

1 . Marque un punto en el círculo unitario , si

.

2. ¿En qué cuarto del plano de coordenadas se encuentra el punto , si es igual a:

3. Marcar puntos en el círculo trigonométrico. , si:

4. Llevar la expresión a funciones trigonométricasyocuarteles.

a)
, b)
, en)

5. Dado el arco MR.METRO - medioyocuarto trimestre,R - medioYocuarto trimestre. Restringir el valor de una variablet para: (componer una desigualdad doble) a) arco MP; b) arcos RM.

6. Escribe una desigualdad doble para las secciones seleccionadas del gráfico:

Arroz. una

7. Resolver desigualdades
,
,
,
.

8. Convertir expresión .

En la segunda etapa de aprendizaje para resolver desigualdades trigonométricas, podemos ofrecer las siguientes recomendaciones relacionadas con la metodología para organizar las actividades de los estudiantes. Al mismo tiempo, es necesario centrarse en las habilidades de los estudiantes para trabajar con un círculo o gráfico trigonométrico, que se forman durante la solución de las ecuaciones trigonométricas más simples.

Primero, es posible motivar la conveniencia de obtener un método general para resolver las desigualdades trigonométricas más simples al referirse, por ejemplo, a una desigualdad de la forma
. Usando los conocimientos y habilidades adquiridos en la etapa preparatoria, los estudiantes llevarán la desigualdad propuesta a la forma
, pero puede resultarle difícil encontrar un conjunto de soluciones a la desigualdad resultante, ya que es imposible resolverlo solo usando las propiedades de la función seno. Esta dificultad se puede evitar consultando la ilustración adecuada (solución de la ecuación gráficamente o utilizando un círculo unitario).

En segundo lugar, el maestro debe llamar la atención de los estudiantes sobre las diferentes formas de completar la tarea, dar un ejemplo apropiado de resolver la desigualdad tanto gráficamente como usando el círculo trigonométrico.

Considere tales opciones para resolver la desigualdad.
.

1. Resolviendo la desigualdad usando el círculo unitario.

En la primera lección sobre resolución de desigualdades trigonométricas, ofreceremos a los estudiantes un algoritmo de solución detallado, que en una presentación paso a paso refleja todas las habilidades básicas necesarias para resolver la desigualdad.

Paso 1.Dibuja un círculo unitario, marca un punto en el eje y y dibuja una línea recta a través de él paralela al eje x. Esta línea cortará el círculo unitario en dos puntos. Cada uno de estos puntos representa números cuyo seno es igual a .

Paso 2Esta línea recta dividía el círculo en dos arcos. Destaquemos aquel en el que se muestran números que tienen un seno mayor que . Naturalmente, este arco se encuentra por encima de la línea recta dibujada.

Arroz. 2

Paso 3Elijamos uno de los extremos del arco marcado. Escribamos uno de los números que está representado por este punto del círculo unitario .

Paso 4Para elegir un número correspondiente al segundo extremo del arco seleccionado, "pasamos" a lo largo de este arco desde el extremo mencionado al otro. Al mismo tiempo, recordamos que al movernos en sentido contrario a las agujas del reloj, los números por los que pasaremos aumentan (al movernos en sentido contrario, los números disminuirían). Escribamos el número que está representado en el círculo unitario por el segundo extremo del arco marcado. .

Por lo tanto, vemos que la desigualdad
satisfacer los números para los cuales la desigualdad
. Resolvimos la desigualdad para números ubicados en el mismo período de la función seno. Por lo tanto, todas las soluciones de la desigualdad se pueden escribir como

Se debe pedir a los estudiantes que consideren cuidadosamente la figura y averigüen por qué todas las soluciones a la desigualdad
se puede escribir en la forma
,
.

Arroz. 3

Es necesario llamar la atención de los estudiantes sobre el hecho de que al resolver desigualdades para la función coseno, dibujamos una línea recta paralela al eje y.

Manera gráfica de resolver la desigualdad.

Gráficos de construcción
y
, dado que
.

Arroz. cuatro

Luego escribimos la ecuación
y su decisión
,
,
, encontrado usando fórmulas
,
,
.

(Donaciónnorte valores 0, 1, 2, encontramos tres raíces de la ecuación compuesta). Valores
son tres abscisas consecutivas de los puntos de intersección de las gráficas
y
. Obviamente, siempre en el intervalo
la desigualdad
, y en el intervalo
- desigualdad
. Nos interesa el primer caso, y luego sumando a los extremos de este intervalo un número que es múltiplo del período del seno, obtenemos una solución a la desigualdad
como:
,
.

Arroz. 5

Resumir. Para resolver la desigualdad
, necesitas escribir la ecuación correspondiente y resolverla. A partir de la fórmula resultante hallar las raíces y , y escribe la respuesta de la desigualdad en la forma: ,
.

En tercer lugar, el hecho sobre el conjunto de raíces de la desigualdad trigonométrica correspondiente se confirma muy claramente al resolverlo gráficamente.

Arroz. 6

Es necesario demostrar a los estudiantes que la bobina, que es la solución de la desigualdad, se repite en el mismo intervalo, igual al período de la función trigonométrica. También puedes considerar una ilustración similar para la gráfica de la función seno.

En cuarto lugar, es recomendable realizar un trabajo de actualización de los métodos de los estudiantes para convertir la suma (diferencia) de funciones trigonométricas en un producto, para llamar la atención de los escolares sobre el papel de estas técnicas en la resolución de desigualdades trigonométricas.

Dicho trabajo puede organizarse a través del cumplimiento autónomo por parte de los alumnos de las tareas propuestas por el profesor, entre las que destacamos las siguientes:

Quinto, se debe pedir a los estudiantes que ilustren la solución de cada desigualdad trigonométrica simple usando un gráfico o un círculo trigonométrico. Asegúrese de prestar atención a su conveniencia, especialmente al uso de un círculo, ya que al resolver desigualdades trigonométricas, la ilustración correspondiente sirve como un medio muy conveniente para fijar el conjunto de soluciones a una desigualdad dada.

Familiarización de los estudiantes con métodos para resolver desigualdades trigonométricas que no son las más simples, es recomendable llevar a cabo de acuerdo con el siguiente esquema: refiriéndose a una desigualdad trigonométrica específica refiriéndose a la ecuación trigonométrica correspondiente búsqueda conjunta (profesor - estudiantes) para una solución independiente transferencia de la técnica encontrada a otras desigualdades del mismo tipo.

Para sistematizar el conocimiento de trigonometría de los estudiantes, recomendamos seleccionar específicamente dichas desigualdades, cuya solución requiere varias transformaciones que pueden implementarse en el proceso de resolución, enfocando la atención de los estudiantes en sus características.

Como tales desigualdades productivas, podemos proponer, por ejemplo, las siguientes:

En conclusión, damos un ejemplo de un conjunto de problemas para resolver desigualdades trigonométricas.

1. Resuelve las desigualdades:

a)
, satisfaciendo la condición
;

b)
, satisfaciendo la condición
.

5. Encuentra todas las soluciones de las desigualdades:

a) ;

b) ;

en)
;

GRAMO)
;

mi)
.

6. Resuelve las desigualdades:

a) ;

b) ;

en) ;

GRAMO)
;

mi) ;

mi) ;

y)
.

7. Resuelve las desigualdades:

a)
;

b) ;

en) ;

G) .

8. Resuelve las desigualdades:

a) ;

b) ;

en) ;

GRAMO)
;

mi)
;

mi) ;

y)
;

h) .

Es recomendable ofrecer las tareas 6 y 7 a los estudiantes que estudian matemáticas en un nivel avanzado, la tarea 8, a los estudiantes en clases con un estudio profundo de las matemáticas.

§3. Métodos especiales para resolver desigualdades trigonométricas

Métodos especiales para resolver ecuaciones trigonométricas, es decir, aquellos métodos que solo pueden usarse para resolver ecuaciones trigonométricas. Estos métodos se basan en el uso de las propiedades de las funciones trigonométricas, así como en el uso de varias fórmulas e identidades trigonométricas.

3.1. Método de sector

Considere el método del sector para resolver desigualdades trigonométricas. Solución de desigualdades de la forma

, dóndePAGS ( X ) yq ( X ) - funciones trigonométricas racionales (senos, cosenos, tangentes y cotangentes entran en ellas racionalmente), de manera similar a la solución de desigualdades racionales. Es conveniente resolver las desigualdades racionales por el método de los intervalos sobre el eje real. Su análogo en la resolución de desigualdades trigonométricas racionales es el método de los sectores en un círculo trigonométrico, porsenx ycosx (
) o un semicírculo trigonométrico paratgx yctgx (
).

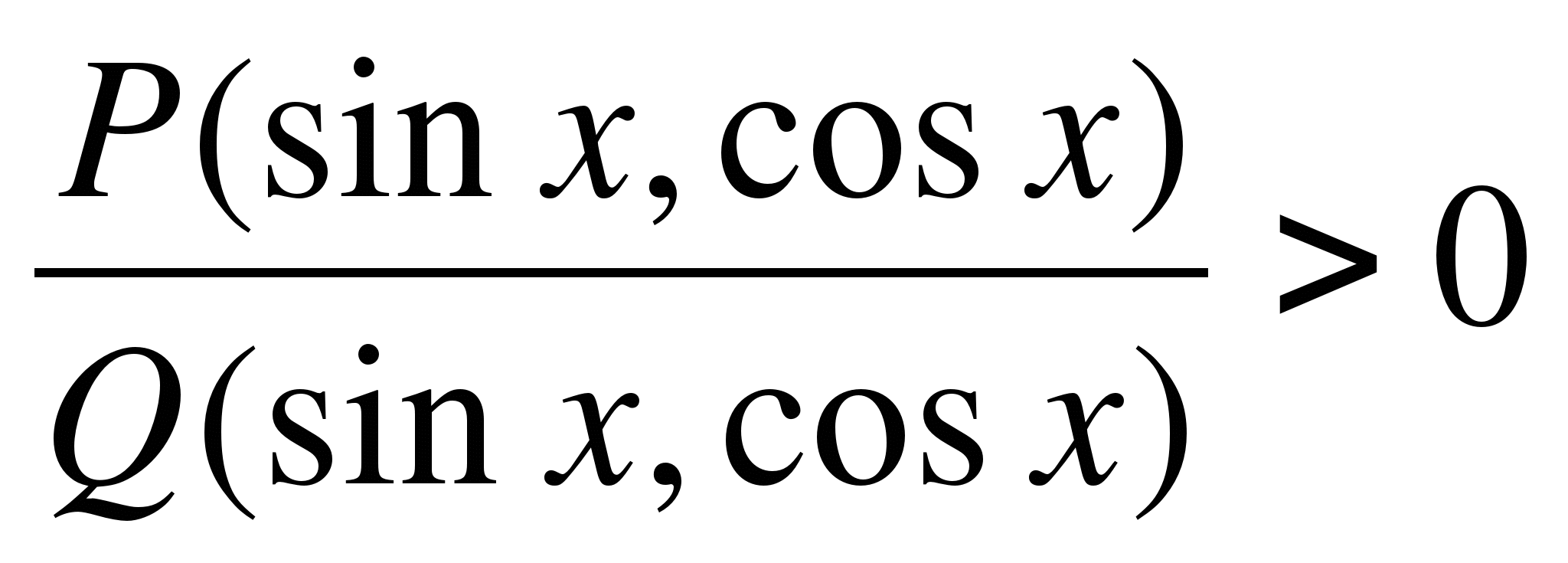
En el método de intervalo, cada factor lineal del numerador y denominador de la forma
punto en el eje numérico , y al pasar por este punto
cambia de signo. En el método del sector, cada multiplicador de la forma
, dónde
- una de las funcionessenx ocosx y
, en un círculo trigonométrico corresponden dos ángulos y
, que dividen el círculo en dos sectores. al pasar y función
cambia de signo.

Debe recordarse lo siguiente:

a) Multiplicadores de la forma
y
, dónde
, conservar el signo para todos los valores . Dichos multiplicadores del numerador y el denominador se descartan, cambiando (si
) para cada rechazo, se invierte el signo de desigualdad.

b) Multiplicadores de la forma
y
también se desechan. Además, si estos son factores del denominador, entonces las desigualdades de la forma se agregan al sistema equivalente de desigualdades
y
. Si estos son factores del numerador, entonces en el sistema equivalente de restricciones corresponden a las desigualdades
y
en el caso de estricta desigualdad inicial, e igualdad
y
en el caso de una desigualdad inicial no estricta. Al soltar el multiplicador
o
el signo de desigualdad se invierte.

Ejemplo 1 Resolver desigualdades: a)
, b)
. tenemos una función, b). Resolver la desigualdad Tenemos

3.2. Método de círculos concéntricos

Este método es análogo al método de ejes numéricos paralelos en la resolución de sistemas de desigualdades racionales.

Considere un ejemplo de un sistema de desigualdades.

Ejemplo 5 Resolver un sistema de desigualdades trigonométricas simples

Primero, resolvemos cada desigualdad por separado (Figura 5). En la esquina superior derecha de la figura, indicaremos para qué argumento se considera el círculo trigonométrico.

Figura 5

A continuación, construimos un sistema de círculos concéntricos para el argumentoX . Dibujamos un círculo y lo sombreamos según la solución de la primera desigualdad, luego dibujamos un círculo de mayor radio y lo sombreamos según la solución de la segunda, luego construimos un círculo para la tercera desigualdad y un círculo base . Dibujamos rayos desde el centro del sistema a través de los extremos de los arcos para que se crucen con todos los círculos. Formamos una solución en el círculo base (Figura 6).

Figura 6

Responder:
,
.

Conclusión

Se completaron todos los objetivos del trabajo de curso. Se sistematiza el material teórico: se dan los principales tipos de desigualdades trigonométricas y los principales métodos para su solución (gráfico, algebraico, método de los intervalos, sectores y el método de los círculos concéntricos). Para cada método, se dio un ejemplo de resolución de una desigualdad. A la parte teórica le siguió la parte práctica. Contiene un conjunto de tareas para resolver desigualdades trigonométricas.

Este trabajo de curso puede ser utilizado por los estudiantes para el trabajo independiente. Los alumnos pueden comprobar el nivel de asimilación de este tema, practicar en la realización de tareas de diversa complejidad.

Habiendo trabajado a través de la literatura relevante sobre este tema, obviamente, podemos concluir que la capacidad y las habilidades para resolver desigualdades trigonométricas en el curso escolar de álgebra y el comienzo del análisis son muy importantes, cuyo desarrollo requiere un esfuerzo considerable por parte de el profesor de matematicas

Por lo tanto, este trabajo será de utilidad para los profesores de matemáticas, ya que permite organizar de manera efectiva la formación de los estudiantes en el tema "Desigualdades trigonométricas".

Se puede continuar el estudio ampliándolo al trabajo final de calificación..

Lista de literatura usada

Bogomolov, NV Colección de problemas de matemáticas [Texto] / N.V. Bogomolov. – M.: Avutarda, 2009. – 206 p.

Vygodsky, M. Ya. Manual de matemáticas elementales [Texto] / M.Ya. Vygodsky. – M.: Avutarda, 2006. – 509 p.

Zhurbenko, L. N. Matemáticas en ejemplos y tareas [Texto] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.

Ivanov, O. A. Matemáticas elementales para escolares, estudiantes y profesores [Texto] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.

Karp, AP Tareas de álgebra e inicios de análisis para la organización de la repetición final y certificación en el grado 11 [Texto] / A.P. Carpa. – M.: Ilustración, 2005. – 79 p.

Kulanin, E.D. 3000 problemas competitivos en matemáticas [Texto] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.

Leibson, K. L. Colección de tareas prácticas en matemáticas [Texto] / K.L. Leibson. – M.: Avutarda, 2010. – 182 p.

Codo, V.V. Problemas con parámetros y su solución. Trigonometría: ecuaciones, desigualdades, sistemas. Grado 10 [Texto] / V.V. Codo. – M.: ARKTI, 2008. – 64 p.

Manova, A.N. Matemáticas. Tutor express para preparar el examen: cuenta. subsidio [Texto] / A.N. Manova. - Rostov del Don: Phoenix, 2012. - 541 p.

Mordkovich, A.G. Álgebra y comienzo del análisis matemático. 10-11 grados. Libro de texto para estudiantes de instituciones educativas [Texto] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 p.

Novikov, A.I. Funciones trigonométricas, ecuaciones y desigualdades [Texto] / I.A. Nóvikov. - M.: FIZMATLIT, 2010. - 260 p.

Oganesyan, V. A. Métodos de enseñanza de las matemáticas en la escuela secundaria: Metodología general. proc. Subsidio para estudiantes de física. - estera falso ped. en-camarada. [Texto] / V. A. Oganesyan. – M.: Ilustración, 2006. – 368 p.

Olechnik, S. N. Ecuaciones y desigualdades. Métodos de solución no estándar [Texto] / S.N. Olekhnik. - M.: Editorial Factorial, 1997. - 219 p.

Sevryukov, P. F. Ecuaciones y desigualdades trigonométricas, exponenciales y logarítmicas [Texto] / P.F. Sevryukov. – M.: Educación Nacional, 2008. – 352 p.

Sergeev, I. N. USO: 1000 tareas con respuestas y soluciones en matemáticas. Todas las tareas del grupo C [Texto] / I.N. sergeev. – M.: Examen, 2012. – 301 p.

Sobolev, A. B. Matemática elemental [Texto] / A.B. Sobolev. - Ekaterimburgo: GOU VPO USTU-UPI, 2005. - 81 p.

Fenko, L. M. El método de los intervalos para resolver desigualdades y estudiar funciones [Texto] / L.M. Fenko. – M.: Avutarda, 2005. – 124 p.

Friedman, L. M. Fundamentos teóricos de la metodología de la enseñanza de las matemáticas [Texto] / L.M. Friedman. - M .: Casa del libro "LIBROKOM", 2009. - 248 p.

Anexo 1

Interpretación gráfica de soluciones a las desigualdades más simples

Arroz. una

Arroz. 2

Fig. 3

Figura 4

Figura 5

Figura 6

Figura 7

Figura 8

Apéndice 2

Soluciones a las desigualdades más simples.

A la mayoría de los estudiantes no les gustan las desigualdades trigonométricas. Pero en vano. Como solía decir un personaje,

“Simplemente no sabes cómo cocinarlos”

Entonces, cómo "cocinar" y con qué presentar una desigualdad con un seno, lo resolveremos en este artículo. Resolveremos de la manera más simple: usando un círculo unitario.

Entonces, lo primero es lo primero, necesitamos el siguiente algoritmo.

Algoritmo para resolver desigualdades con seno:

1. coloque el número $a$ en el eje del seno y dibuje una línea recta paralela al eje del coseno hasta que se cruce con el círculo;
2. los puntos de intersección de esta línea con el círculo se rellenarán si la desigualdad no es estricta, y no se rellenarán si la desigualdad es estricta;
3. el área de solución de la desigualdad será arriba de la línea y hasta el círculo si la desigualdad contiene el signo “$>$”, y debajo de la línea y hasta el círculo si la desigualdad contiene el signo “$<$”;
4. para encontrar los puntos de intersección, resolvemos la ecuación trigonométrica $\sin(x)=a$, obtenemos $x=(-1)^(n)\arcsin(a) + \pi n$;
5. configurando $n=0$, encontramos el primer punto de intersección (se encuentra en el primer o en el cuarto cuadrante);
6. para encontrar el segundo punto, miramos en qué dirección cruzamos el área hasta el segundo punto de intersección: si es en dirección positiva, entonces se debe tomar $n=1$, y si es en dirección negativa, entonces $n=- 1$;
7. en respuesta, se escribe el intervalo desde el punto de intersección más pequeño $+ 2\pi n$ hasta el más grande $+ 2\pi n$.

Limitación del algoritmo

importante :d este algoritmo No funciona para desigualdades de la forma $\sin(x) > 1; \ \sin(x) \geq 1, \ \sin(x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$.

Casos especiales al resolver una desigualdad con un seno

También es importante tener en cuenta los siguientes casos, que son mucho más convenientes para resolver lógicamente sin usar el algoritmo anterior.

Caso especial 1. Resuelve la desigualdad:

$\sin(x) \leq 1.$

Dado que el dominio de la función trigonométrica $y=\sin(x)$ es como máximo $1$, el lado izquierdo de la desigualdad para cualquier$x$ del dominio (y el dominio del seno son todos los números reales) no es mayor que $1$. Y, por tanto, en respuesta escribimos: $x \in R$.

Consecuencia:

$\sin(x) \geq -1.$

Caso especial 2. Resuelve la desigualdad:

$\pecado(x)< 1.$

Aplicando argumentos similares al caso especial 1, obtenemos que el lado izquierdo de la desigualdad es menor que $1$ para todo $x \in R$, excepto para los puntos que son solución de la ecuación $\sin(x) = 1$. Resolviendo esta ecuación, tendremos:

$x = (-1)^(n)\arcsin(1)+ \pi n = (-1)^(n)\frac(\pi)(2) + \pi n.$

Y, por lo tanto, en respuesta escribimos: $x \in R \backslash \left\((-1)^(n)\frac(\pi)(2) + \pi n\right\)$.

Consecuencia: la desigualdad se resuelve de manera similar

$\sin(x) > -1.$

Ejemplos de resolución de desigualdades usando un algoritmo.

Ejemplo 1: Resuelve la desigualdad:

$\sen(x) \geq \frac(1)(2).$

1. Tenga en cuenta la coordenada $\frac(1)(2)$ en el eje del seno.
2. Dibuja una recta paralela al eje del coseno y que pase por este punto.
3. Tenga en cuenta los puntos de intersección. Estarán sombreados porque la desigualdad no es estricta.
4. El signo de desigualdad es $\geq$, lo que significa que pintamos sobre el área por encima de la línea, es decir, semicírculo más pequeño.
5. Encuentre el primer punto de intersección. Para hacer esto, convierte la desigualdad en una igualdad y resuélvela: $\sin(x)=\frac(1)(2) \ \Rightarrow \ x=(-1)^(n)\arcsin(\frac(1 )(2) )+\pi n =(-1)^(n)\frac(\pi)(6) + \pi n$. Además establecemos $n=0$ y encontramos el primer punto de intersección: $x_(1)=\frac(\pi)(6)$.
6. Encontramos el segundo punto. Nuestra área va en la dirección positiva desde el primer punto, por lo que igualamos $n$ a $1$: $x_(2)=(-1)^(1)\frac(\pi)(6) + \pi \ cpunto 1 = \ pi - \frac(\pi)(6) = \frac(5\pi)(6)$.

Así, la solución tomará la forma:

$x \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\right], \ n \in Z.$

Ejemplo 2: Resuelve la desigualdad:

$\pecado(x)< -\frac{1}{2}$

Marcamos la coordenada $- \frac(1)(2)$ en el eje del seno y trazamos una recta paralela al eje del coseno y que pasa por este punto. Tenga en cuenta los puntos de intersección. No se sombrearán, ya que la desigualdad es estricta. Signo de desigualdad $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его:

$\sin(x)=-\frac(1)(2)$

$x=(-1)^(n)\arcsin(\left(-\frac(1)(2)\right))+ \pi n =(-1)^(n+1)\frac(\pi )(6) + \pi n$.

Ajustando más $n=0$, encontramos el primer punto de intersección: $x_(1)=-\frac(\pi)(6)$. Nuestra área va en dirección negativa desde el primer punto, por lo que establecemos $n$ igual a $-1$: $x_(2)=(-1)^(-1+1)\frac(\pi)(6 ) + \pi \cdot (-1) = -\pi + \frac(\pi)(6) = -\frac(5\pi)(6)$.

Entonces, la solución a esta desigualdad será el intervalo:

$x \in \left(-\frac(5\pi)(6) + 2\pi n; -\frac(\pi)(6) + 2 \pi n\right), \ n \in Z.$

Ejemplo 3: Resuelve la desigualdad:

$1 – 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \leq 0.$

Este ejemplo no se puede resolver inmediatamente usando un algoritmo. Primero necesitas convertirlo. Hacemos exactamente lo que haríamos con la ecuación, pero no nos olvidemos del signo. ¡Dividir o multiplicar por un número negativo lo invierte!

Entonces, movamos todo lo que no contenga una función trigonométrica hacia el lado derecho. Obtenemos:

$- 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \leq -1.$

Divide los lados izquierdo y derecho entre $-2$ (¡no te olvides del signo!). Tendrá:

$\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \geq \frac(1)(2).$

De nuevo, tenemos una desigualdad que no podemos resolver usando el algoritmo. Pero aquí basta con hacer un cambio de variable:

$t=\frac(x)(4)+\frac(\pi)(6).$

Obtenemos una desigualdad trigonométrica, que se puede resolver usando el algoritmo:

$\sin(t) \geq \frac(1)(2).$

Esta desigualdad se resolvió en el ejemplo 1, por lo que tomaremos prestada la respuesta de allí:

$t \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\derecha].$

Sin embargo, la decisión aún no ha terminado. Necesitamos volver a la variable original.

$(\frac(x)(4)+\frac(\pi)(6)) \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\derecha].$

Representemos la brecha como un sistema:

$\left\(\begin(array)(c) \frac(x)(4)+\frac(\pi)(6) \geq \frac(\pi)(6) + 2\pi n, \\ \frac(x)(4)+\frac(\pi)(6) \leq \frac(5\pi)(6) + 2 \pi n.\end(arreglo) \right.$

En el lado izquierdo del sistema hay una expresión ($\frac(x)(4)+\frac(\pi)(6)$), que pertenece al intervalo. El límite izquierdo del intervalo es responsable de la primera desigualdad y el límite derecho es responsable de la segunda. Además, los corchetes juegan un papel importante: si el corchete es cuadrado, entonces la desigualdad será no estricta, y si es redonda, será estricta. nuestra tarea es obtener $x$ a la izquierda en ambas desigualdades.

Muevamos $\frac(\pi)(6)$ del lado izquierdo al lado derecho, obtenemos:

$\left\(\begin(matriz)(c) \frac(x)(4) \geq \frac(\pi)(6) + 2\pi n -\frac(\pi)(6), \\ \frac(x)(4) \leq \frac(5\pi)(6) + 2 \pi n – \frac(\pi)(6).\end(matriz) \right.$

Simplificando, tendremos:

$\left\(\begin(arreglo)(c) \frac(x)(4) \geq 2\pi n, \\ \frac(x)(4) \leq \frac(2\pi)(3) + 2 \pi n.\end(matriz) \right.$

Multiplicando los lados izquierdo y derecho por $4$, obtenemos:

$\left\(\begin(array)(c) x \geq 8\pi n, \\ x \leq \frac(8\pi)(3) + 8 \pi n. \end(array) \right. ps

Al ensamblar el sistema en un intervalo, obtenemos la respuesta:

$x \in \left[ 8\pi n; \frac(8\pi)(3) + 8 \pi n\right], \ n \in Z.$

1.5 Desigualdades trigonométricas y métodos para su solución

1.5.1 Resolver desigualdades trigonométricas simples

La mayoría de los autores de libros de texto modernos sobre matemáticas sugieren que comencemos nuestra consideración de este tema resolviendo las desigualdades trigonométricas más simples. El principio de resolver las desigualdades trigonométricas más simples se basa en el conocimiento y la capacidad de determinar en un círculo trigonométrico los valores no solo de los ángulos trigonométricos principales, sino también de otros valores.

Mientras tanto, la solución de desigualdades de la forma , , , se puede realizar de la siguiente manera: primero, encontramos algún intervalo () en el que esta desigualdad sea verdadera, y luego escribimos la respuesta final sumando a los extremos de la encontrada intervalo un múltiplo del período del seno o coseno: ( ). En este caso, el valor se encuentra fácilmente, porque o . La búsqueda de un valor se basa en la intuición de los estudiantes, su capacidad para notar la igualdad de arcos o segmentos, utilizando la simetría de partes individuales del gráfico de seno o coseno. Y esto a veces está más allá del poder de un número bastante grande de estudiantes. Para superar las dificultades señaladas, en los últimos años los libros de texto han utilizado un enfoque diferente para resolver las desigualdades trigonométricas más simples, pero esto no mejoró los resultados del aprendizaje.

Durante varios años, hemos utilizado con bastante éxito las fórmulas de las raíces de las ecuaciones correspondientes para encontrar soluciones a las desigualdades trigonométricas.

Estudiamos este tema de la siguiente manera:

1. Construimos gráficos y y \u003d a, asumiendo que .

Luego escribimos la ecuación y su solución. Dando n 0; una; 2, encontramos tres raíces de la ecuación compuesta: . Los valores son las abscisas de tres puntos de intersección consecutivos de las gráficas y y = a. es obvio que la desigualdad siempre se cumple en el intervalo (), y en el intervalo () - la desigualdad.

Sumando a los extremos de estos intervalos un número que es múltiplo del período del seno, en el primer caso obtenemos la solución de la desigualdad en la forma: ; y en el segundo caso, la solución de la desigualdad en la forma:

Solo en contraste con el seno de la fórmula, que es una solución a la ecuación, para n = 0 obtenemos dos raíces y la tercera raíz para n = 1 en la forma . Y de nuevo son tres abscisas consecutivas de los puntos de intersección de las gráficas y . En el intervalo () se cumple la desigualdad, en el intervalo () la desigualdad

Ahora es fácil escribir las soluciones de las desigualdades y . En el primer caso, obtenemos: ;

y en el segundo: .

Resumir. Para resolver la desigualdad o , es necesario componer la ecuación correspondiente y resolverla. A partir de la fórmula resultante, encuentra las raíces y , y escribe la respuesta de la desigualdad en la forma: .

Al resolver desigualdades , a partir de la fórmula de las raíces de la ecuación correspondiente encontramos las raíces y , y escribimos la respuesta de la desigualdad en la forma: .

Esta técnica le permite enseñar a todos los estudiantes cómo resolver desigualdades trigonométricas. esta técnica se basa completamente en las habilidades que los estudiantes han dominado firmemente. Estos son la capacidad de resolver los más simples y encontrar el valor de una variable usando una fórmula. Además, se vuelve completamente opcional resolver cuidadosamente una gran cantidad de ejercicios bajo la guía de un maestro para demostrar todo tipo de técnicas de razonamiento según el signo de la desigualdad, el valor del módulo del número a y su signo. Y el proceso mismo de resolver la desigualdad se vuelve breve y, lo que es muy importante, uniforme.

Otra ventaja de este método es que facilita la resolución de desigualdades incluso cuando el lado derecho no es un valor de tabla de seno o coseno.

Demostremos esto con un ejemplo específico. Sea necesario resolver la desigualdad. Escribamos la ecuación correspondiente y resolvámosla:

Encontremos los valores de y .

Para n = 1

Para n = 2

Escribimos la respuesta final a esta desigualdad:

En el ejemplo considerado de resolver las desigualdades trigonométricas más simples, solo puede haber un inconveniente: la presencia de una cierta cantidad de formalismo. Pero si todo se evalúa solo desde estas posiciones, será posible acusar de formalismo tanto a las fórmulas de las raíces de la ecuación cuadrática como a todas las fórmulas para resolver ecuaciones trigonométricas, y mucho más.

El método propuesto, si bien ocupa un lugar digno en la formación de habilidades y destrezas para la resolución de desigualdades trigonométricas, no se puede subestimar la importancia y características de otros métodos para la resolución de desigualdades trigonométricas. Esto incluye el método de intervalo.

Consideremos su esencia.

Conjunto editado por A.G. Mordkovich, aunque tampoco se deben ignorar otros libros de texto. § 3. Métodos para enseñar el tema "Funciones trigonométricas" en el curso de álgebra y el comienzo del análisis En el estudio de las funciones trigonométricas en la escuela, se pueden distinguir dos etapas principales: ü Conocimiento inicial de las funciones trigonométricas ...

Durante la investigación se resolvieron las siguientes tareas: 1) Se analizaron los libros de texto actuales de álgebra y los inicios del análisis matemático para identificar los métodos para resolver las ecuaciones irracionales y las desigualdades presentadas en ellos. El análisis realizado nos permite sacar las siguientes conclusiones: En la escuela secundaria no se presta suficiente atención a los métodos para resolver diversas ecuaciones irracionales, principalmente...