Clase 3 Teoremas generales de la dinámica

Dinámica del sistema de puntos materiales. es una rama importante de la mecánica teórica. Aquí, consideramos principalmente problemas del movimiento de sistemas mecánicos (sistemas de puntos materiales) con un número finito de grados de libertad - el número máximo de parámetros independientes que determinan la posición del sistema. La tarea principal de la dinámica de sistemas es el estudio de las leyes de movimiento de un cuerpo rígido y sistemas mecánicos.

El enfoque más simple para estudiar el movimiento de un sistema, que consiste en norte puntos materiales, se reduce a la consideración de los movimientos de cada punto individual del sistema. En este caso, se deben determinar todas las fuerzas que actúan sobre cada punto del sistema, incluidas las fuerzas de interacción entre puntos.

Determinando la aceleración de cada punto de acuerdo con la segunda ley de Newton (1.2), obtenemos para cada punto tres leyes de movimiento diferenciales escalares de segundo orden, es decir 3 norte ley diferencial de movimiento para todo el sistema.

Para encontrar las ecuaciones de movimiento de un sistema mecánico para fuerzas dadas y condiciones iniciales para cada punto del sistema, se deben integrar las leyes diferenciales obtenidas. Esta tarea es difícil incluso en el caso de dos puntos materiales que se mueven únicamente bajo la acción de fuerzas de interacción según la ley de atracción universal (problema de los dos cuerpos), y extremadamente difícil en el caso de tres puntos que interactúan (problema de los tres cuerpos). ).

Por lo tanto, es necesario encontrar tales métodos para resolver problemas que conduzcan a ecuaciones solucionables y den una idea del movimiento de un sistema mecánico. Los teoremas generales de la dinámica, al ser consecuencia de las leyes diferenciales del movimiento, permiten evitar la complejidad que surge durante la integración y obtener los resultados necesarios.

3.1 Observaciones generales

Los puntos del sistema mecánico estarán numerados por índices i, j, k etc. que recorren todos los valores 1, 2, 3… norte, dónde norte es el número de puntos del sistema. Magnitudes físicas relacionadas con k El punto se denota con el mismo índice que el punto. Por ejemplo, expresan respectivamente el radio vector y la velocidad k-ésimo punto.

Sobre cada uno de los puntos del sistema actúan fuerzas de dos orígenes: por un lado, fuerzas cuyo origen se encuentra fuera del sistema, denominadas externo fuerzas y denotado por ; en segundo lugar, fuerzas de otros puntos de este sistema, llamados interno fuerzas y denotado por . Las fuerzas internas satisfacen la tercera ley de Newton. Considere las propiedades más simples de las fuerzas internas que actúan sobre todo el sistema mecánico en cualquiera de sus estados.

Primera propiedad. La suma geométrica de todas las fuerzas internas del sistema (el principal vector de fuerzas internas) es igual a cero.

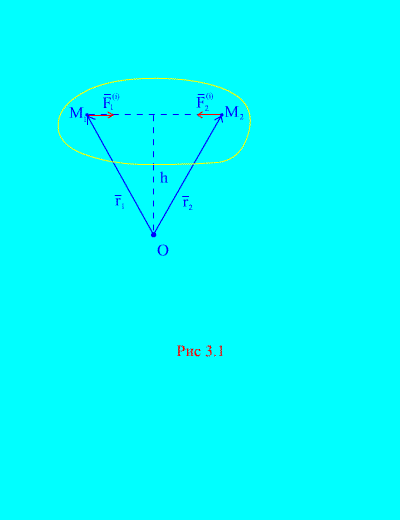
De hecho, si consideramos cualesquiera dos puntos arbitrarios del sistema, por ejemplo, y (Figura 3.1), entonces para ellos , porque las fuerzas de acción y reacción son siempre iguales en valor absoluto, actúan a lo largo de una línea de acción en dirección opuesta, que conecta los puntos que interactúan. El principal vector de fuerzas internas consta de pares de fuerzas de puntos que interactúan, por lo tanto

(3.1)

Segunda propiedad. La suma geométrica de los momentos de todas las fuerzas internas relativas a un punto arbitrario en el espacio es cero.

Considere el sistema de momentos de fuerzas y con respecto al punto O(Figura 3.1). De (Figura 3.1). está claro que

,

porque ambas fuerzas tienen los mismos brazos y direcciones opuestas de momentos vectoriales. El momento principal de las fuerzas internas sobre el punto. O consiste en la suma vectorial de tales expresiones y es igual a cero. Como consecuencia,

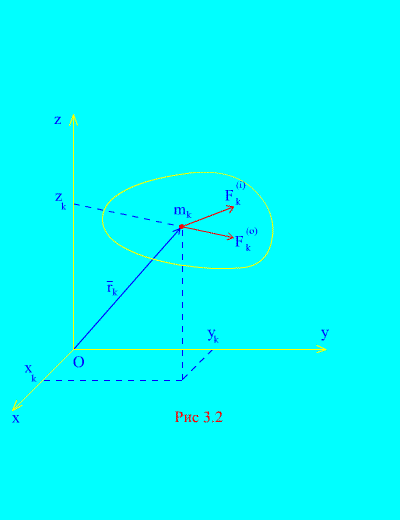
Sean fuerzas externas e internas que actúan sobre un sistema mecánico que consta de norte puntos (Figura 3.2). Si la resultante de las fuerzas externas y la resultante de todas las fuerzas internas se aplican a cada punto del sistema, entonces para cualquier k th punto del sistema, uno puede componer ecuaciones diferenciales de movimiento. En total tales ecuaciones serán norte:

y en proyecciones sobre ejes de coordenadas fijos 3 norte:

(3.4)

Las ecuaciones vectoriales (3.3) o las ecuaciones escalares equivalentes (3.4) representan las leyes diferenciales de movimiento de los puntos materiales de todo el sistema. Si todos los puntos se mueven paralelos a un plano o una línea recta, entonces el número de ecuaciones (3.4) en el primer caso será 2 norte, en el segundo norte.

Ejemplo 1 Dos cargas de masa y están interconectadas por un cable inextensible tirado sobre un bloque (Figura 3.3). Despreciando las fuerzas de fricción, así como la masa del bloque y el cable, determine la ley de movimiento de mercancías y la tensión del cable.

Solución. El sistema consta de dos cuerpos materiales (conectados por un cable inextensible) que se mueven paralelos a un eje X. Escribamos las leyes diferenciales del movimiento en proyecciones sobre el eje X para todos.

Deje que el peso derecho descienda con aceleración, luego el peso izquierdo subirá con aceleración. Nos liberamos mentalmente de la conexión (cable) y la reemplazamos con reacciones y (Figura 3.3). Suponiendo que los cuerpos son libres, compondremos las leyes diferenciales del movimiento en la proyección sobre el eje X(lo que significa que las tensiones del hilo son fuerzas internas y el peso de las cargas es externo):

Como y (los cuerpos están conectados por un cable inextensible), obtenemos

Resolviendo estas ecuaciones para la aceleración y tensión del cable T, obtenemos

.

Tenga en cuenta que la tensión del cable en no es igual a la gravedad de la carga correspondiente.

3. 2. El teorema del movimiento del centro de masa

Se sabe que un cuerpo rígido y un sistema mecánico en un plano pueden moverse con bastante dificultad. Se puede llegar al primer teorema sobre el movimiento de un cuerpo y de un sistema mecánico de la siguiente manera: suelte el c.-l. un objeto que consta de muchos cuerpos sólidos unidos entre sí. Está claro que volará en una parábola. Esto se reveló al estudiar el movimiento de un punto. Sin embargo, ahora el objeto no es un punto. Gira, se balancea en el proceso de volar alrededor de algún centro efectivo, que se mueve a lo largo de una parábola. El primer teorema sobre el movimiento de objetos complejos dice que cierto centro efectivo es el centro de masa de un objeto en movimiento. El centro de masa no está necesariamente ubicado en el cuerpo mismo, puede estar en algún lugar fuera de él.

Teorema. El centro de masa de un sistema mecánico se mueve como un punto material con una masa igual a la masa de todo el sistema, sobre el cual se aplican todas las fuerzas externas que actúan sobre el sistema.

Para demostrar el teorema, reescribimos las leyes diferenciales del movimiento (3.3) de la siguiente forma:

(3.5)

dónde norte es el número de puntos del sistema.

Sumemos las ecuaciones término a término:

(a)

La posición del centro de masa del sistema mecánico en relación con el sistema de coordenadas seleccionado está determinada por la fórmula (2.1): dónde METRO es la masa del sistema. Entonces el lado izquierdo de la igualdad (a) se escribe

La primera suma, situada a la derecha de la igualdad (a), es igual al vector principal de las fuerzas externas, y la última, por la propiedad de las fuerzas internas, es igual a cero. Entonces la igualdad (a), teniendo en cuenta (b), se reescribirá

, (3.6)

aquellos. el producto de la masa del sistema y la aceleración del centro de su masa es igual a la suma geométrica de todas las fuerzas externas que actúan sobre el sistema.

De la ecuación (3.6) se deduce que las fuerzas internas no afectan directamente el movimiento del centro de masa. Sin embargo, en algunos casos son la causa de la aparición de fuerzas externas aplicadas al sistema. Así, las fuerzas internas que hacen girar las ruedas motrices del automóvil provocan la acción sobre éste de una fuerza de adherencia externa aplicada a la llanta.

Ejemplo 2 El mecanismo, ubicado en un plano vertical, se instala en un plano horizontal liso y se une a él con barras rígidamente fijadas a la superficie. A y L (Figura 3.4).

Disco 1 radio R inmóvil. Disco 2 masa metro y radio r sujetado con una manivela, longitud R+ r en el punto Desde 2. La manivela gira a una constante

velocidad angular. En el momento inicial, la manivela ocupaba la posición horizontal derecha. Despreciando la masa de la manivela, determine las fuerzas horizontales y verticales máximas que actúan sobre las barras, si la masa total del marco y la rueda 1 es igual a METRO. Considere también el comportamiento del mecanismo en ausencia de barras.

Solución. El sistema consta de dos masas ( norte=2 ): un disco fijo 1 con un marco y un disco móvil 2. Vamos a dirigir el eje a a través del centro de gravedad del disco fijo verticalmente hacia arriba, el eje X- a lo largo del plano horizontal.

Escribimos el teorema sobre el movimiento del centro de masa (3.6) en la forma de coordenadas

Las fuerzas externas de este sistema son: el peso del marco y el disco fijo - miligramos, peso del disco móvil miligramos, - la reacción horizontal total de los tornillos, - la reacción total normal del plano. Como consecuencia,

Entonces las leyes del movimiento (b) se reescriben

Calculemos las coordenadas del centro de masa del sistema mecánico:

; (GRAMO)

visto desde (Figura 3.4), , , (ángulo de rotación de la manivela), . Sustituyendo estas expresiones en (r) y calculando las segundas derivadas con respecto al tiempo t de , , obtenemos que

(mi)

Sustituyendo (c) y (e) en (b), encontramos

La presión horizontal que actúa sobre las barras es mayor y menor cuando porque = 1 respectivamente, es decir

La presión del mecanismo en el plano horizontal tiene los valores más altos y más bajos cuando pecado respectivamente, es decir

De hecho, el primer problema de la dinámica ha sido resuelto: de acuerdo con las conocidas ecuaciones de movimiento del centro de masa del sistema (e), se restablecen las fuerzas involucradas en el movimiento.

A falta de bares k y L (Figura 3.4), el mecanismo puede comenzar a rebotar por encima del plano horizontal. Esto tendrá lugar cuando , i.e. cuando , se deduce que la velocidad angular de rotación de la manivela, a la que rebota el mecanismo, debe satisfacer la igualdad

.

3. 3. Ley de conservación del movimiento del centro de masa

Si el vector principal de fuerzas externas que actúan sobre el sistema es igual a cero, es decir , luego de(3.6)se deduce que la aceleración del centro de masa es cero, por lo tanto, la velocidad del centro de masa es constante en magnitud y dirección. Si, en particular, en el momento inicial el centro de masa está en reposo, entonces estará en reposo durante todo el tiempo hasta que el vector principal de fuerzas externas sea igual a cero.

Varios corolarios se derivan de este teorema.

· Las fuerzas internas por sí solas no pueden cambiar la naturaleza del movimiento del centro de masa del sistema.

· Si el vector principal de fuerzas externas que actúan sobre el sistema es igual a cero, entonces el centro de masa está en reposo o se mueve de manera uniforme y rectilínea.

· Si la proyección del vector principal de las fuerzas externas del sistema sobre algún eje fijo es igual a cero, entonces la proyección de la velocidad del centro de masa del sistema sobre este eje no cambia.

· Un par de fuerzas aplicadas a un cuerpo rígido no pueden cambiar el movimiento de su centro de masa (solo pueden hacer que el cuerpo gire alrededor del centro de masa).

Consideremos un ejemplo que ilustra la ley de conservación del movimiento del centro de masa.

Ejemplo 3 Dos pesos con masas y están conectados por un hilo inextensible tirado sobre un bloque (Figura 3.5), fijado en una cuña con masa METRO. La cuña descansa sobre un plano horizontal liso. Inicialmente, el sistema estaba en reposo. Encuentre el desplazamiento de la cuña a lo largo del plano cuando la primera carga se baja a una altura NORTE. Ignore la masa del bloque y el hilo.

Solución. Las fuerzas externas que actúan sobre la cuña junto con los pesos son las fuerzas de gravedad, y miligramos, así como la respuesta normal de una superficie horizontal lisa N. Por lo tanto,

Como el sistema estaba en reposo en el momento inicial, tenemos .

Calculemos la coordenada del centro de masa del sistema en y en el momento t 1 cuando el peso de la carga gramo descender a una altura H.

Por un momento:

,

dónde , , X- respectivamente, las coordenadas del centro de masa de las cargas de peso g, g y peso en cuña METROgramo.

Supongamos que la cuña en el momento del tiempo se mueve en la dirección positiva del eje. Buey por la cantidad L si el peso de la carga cae a una altura NORTE. Entonces, por un momento

porque las cargas junto con la cuña se moverán a L a la derecha, el peso se moverá una distancia hacia arriba en la cuña. Ya que después de los cálculos obtenemos

.

3.4. Sistema de cantidad de movimiento

3.4.1. Cálculo de la cantidad de movimiento de un sistema

La cantidad de movimiento de un punto material es una cantidad vectorial igual al producto de la masa del punto y el vector de su velocidad

Unidad de medida de la cantidad de movimiento -

La cantidad de movimiento de un sistema mecánico se denomina suma vectorial de la cantidad de movimiento de los puntos individuales del sistema, es decir,

dónde norte es el número de puntos del sistema.

La cantidad de movimiento de un sistema mecánico se puede expresar en términos de la masa del sistema METRO y la velocidad del centro de masa. En realidad,

aquellos. la cantidad de movimiento del sistema es igual al producto de la masa de todo el sistema y la velocidad de su centro de masa. La dirección es la misma que la dirección. (Figura 3.6)

En proyecciones sobre ejes rectangulares, tenemos

donde , , - proyecciones de la velocidad del centro de masa del sistema.

Aquí METRO es la masa del sistema mecánico; no cambia a medida que el sistema se mueve.

Es especialmente conveniente usar estos resultados cuando se calculan los momentos de cuerpos rígidos.

Se puede ver a partir de la fórmula (3.7) que si un sistema mecánico se mueve de tal manera que su centro de masa permanece estacionario, entonces la cantidad de movimiento del sistema permanece igual a cero.

3.4.2. Impulso elemental y de fuerza completa

La acción de una fuerza sobre un punto material a lo largo del tiempo. dt puede caracterizarse por un impulso elemental. Impulso total de fuerza en el tiempo t, o impulso de fuerza, está determinado por la fórmula

o en proyecciones sobre las coordenadas del eje

(3.8a)

La unidad de fuerza impulso es .

3.4.3. Teorema sobre el cambio en el impulso del sistema.

Sean aplicadas fuerzas externas e internas a los puntos del sistema. Entonces, para cada punto del sistema, podemos aplicar las leyes diferenciales del movimiento (3.3), teniendo en cuenta que :

.

Sumando todos los puntos del sistema, obtenemos

Por la propiedad de las fuerzas internas y por definición tenemos

(3.9)

Multiplicando ambos lados de esta ecuación por dt, obtenemos el teorema de la variación de la cantidad de movimiento en forma diferencial:

, (3.10)

aquellos. el diferencial de la cantidad de movimiento de un sistema mecánico es igual a la suma vectorial de los impulsos elementales de todas las fuerzas externas que actúan sobre los puntos del sistema mecánico.

Calculando la integral de ambas partes de (3.10) a lo largo del tiempo de 0 a t, obtenemos el teorema en forma finita o integral

(3.11)

En proyecciones sobre los ejes de coordenadas, tendremos

Cambio en el impulso de un sistema mecánico a lo largo del tiempo.t, es igual a la suma vectorial de todos los impulsos de fuerzas externas que actúan sobre los puntos del sistema mecánico en el mismo tiempo.

Ejemplo 4 carga de masa metro desciende por un plano inclinado partiendo del reposo bajo la acción de una fuerza F, proporcional al tiempo: , donde (Figura 3.7). ¿Cuál es la velocidad del cuerpo después de t segundos después del inicio del movimiento, si el coeficiente de fricción por deslizamiento de la carga en el plano inclinado es igual a F.

Solución. Representemos las fuerzas aplicadas a la carga: miligramos - gravedad de la carga, norte es la reacción normal del plano, es la fuerza de fricción por deslizamiento de la carga sobre el plano, y . La dirección de todas las fuerzas se muestra en (Figura 3.7).

Dirijamos el eje X por un plano inclinado. Escribamos el teorema del cambio de cantidad de movimiento (3.11) en la proyección sobre el eje X:

(a)

Por condición, porque en el momento inicial de tiempo, la carga estaba en reposo. La suma de las proyecciones de los impulsos de todas las fuerzas en el eje x es

Como consecuencia,

,

.

3.4.4. Leyes de conservación del momento

Las leyes de conservación se obtienen como casos especiales del teorema del cambio de cantidad de movimiento. Son posibles dos casos especiales.

· Si la suma vectorial de todas las fuerzas externas aplicadas al sistema es igual a cero, es decir , entonces se sigue del teorema (3.9) , qué ,

aquellos. si el vector principal de fuerzas externas del sistema es igual a cero, entonces el momento del sistema es constante en magnitud y dirección.

· Si la proyección del vector principal de fuerzas externas en cualquier eje de coordenadas es igual a cero, por ejemplo, Ox, es decir , entonces la proyección de la cantidad de movimiento en este eje es constante.

Considere un ejemplo de aplicación de la ley de conservación del momento.

Ejemplo 5 Un péndulo balístico es un cuerpo de masa, suspendido de una cuerda larga (Figura 3.8).

Una bala de masa moviéndose a una velocidad V y al caer en un cuerpo inmóvil, queda atrapado en él, y el cuerpo se desvía. ¿Cuál fue la velocidad de la bala si el cuerpo se elevó a una altura h ?

Solución. Deje que el cuerpo con la bala clavada adquiera velocidad. Entonces, usando la ley de conservación de la cantidad de movimiento en la interacción de dos cuerpos, podemos escribir .

La velocidad se puede calcular usando la ley de conservación de la energía mecánica. . Después . Como resultado, encontramos

.

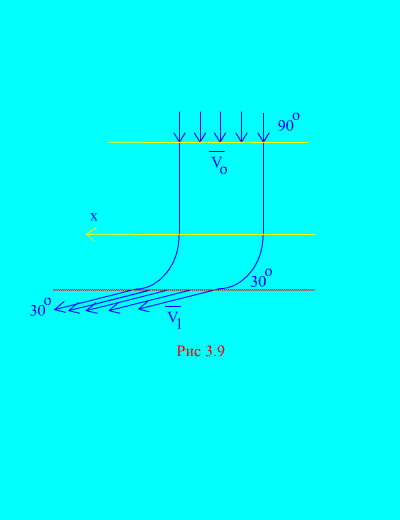
Ejemplo 6. El agua entra en un canal fijo (Figura 3.9) sección variable con una velocidad en ángulo con el horizonte; área de la sección transversal del canal en la entrada; la velocidad del agua a la salida del canal y forma un ángulo con el horizonte.

Determine la componente horizontal de la reacción que ejerce el agua sobre las paredes del canal. densidad del agua .

Solución. Determinaremos la componente horizontal de la reacción que ejercen las paredes del canal sobre el agua. Esta fuerza es igual en valor absoluto y de signo opuesto a la fuerza deseada. Tenemos, según (3.11a),

. (a)

Calculamos la masa del volumen de líquido que ingresa al canal durante el tiempo t:

El valor de rAV 0 se llama segunda masa - la masa de líquido que fluye a través de cualquier sección de la tubería por unidad de tiempo.

La misma cantidad de agua sale del canal en el mismo tiempo. Las velocidades inicial y final se dan en la condición.

Calculemos el lado derecho de la igualdad (a) que determina la suma de las proyecciones sobre el eje horizontal de las fuerzas externas aplicadas al sistema (agua). La única fuerza horizontal es la componente horizontal de la reacción resultante de las paredes. R x. Esta fuerza es constante durante el movimiento constante del agua. Es por eso

. (en)

Sustituyendo (b) y (c) en (a), obtenemos

3.5. Momento cinético del sistema.

3.5.1. Momento principal de la cantidad de movimiento del sistema

Sea el radio vector de un punto con la masa del sistema relativo a un punto A, llamado centro (Figura 3.10).

Momento de cantidad de movimiento (momento cinético) de un punto con respecto al centro A llamado vector , determinado por la fórmula

. (3.12)

En este caso, el vector dirigida perpendicularmente al plano que pasa por el centro PERO y vectores .

Momento de cantidad de movimiento (momento cinético) de un punto sobre un eje se llama la proyección sobre este eje del momento angular del punto relativo a cualquier centro elegido sobre este eje.

El momento principal del momento (momento cinético) del sistema en relación con el centro A se llama la cantidad

(3.13)

El momento principal del momento (momento cinético) del sistema sobre el eje se llama la proyección sobre este eje del momento principal de la cantidad de movimiento del sistema en relación con cualquier elegido en el dado eje central.

3.5.2. Cantidad de movimiento de un cuerpo rígido giratorio sobre el eje de rotación

Punto fijo compatible O cuerpo acostado sobre el eje de rotacion Oz, con el origen del sistema de coordenadas Ohuz, cuyos ejes rotarán con el cuerpo (Figura 3.11). Sea el radio vector del punto del cuerpo relativo al origen de coordenadas, sus proyecciones sobre los ejes se denotarán por , , . Las proyecciones del vector velocidad angular del cuerpo sobre los mismos ejes se denotarán por 0, 0, ().

Considere el movimiento de un determinado sistema de volúmenes materiales en relación con un sistema de coordenadas fijo. Cuando el sistema no es libre, entonces puede considerarse libre, si descartamos las restricciones impuestas al sistema y reemplazamos su acción con las reacciones correspondientes.

Dividamos todas las fuerzas aplicadas al sistema en externas e internas; ambos pueden incluir reacciones de desechos

conexiones Denote por y el vector principal y el momento principal de las fuerzas externas en relación con el punto A.

1. Teorema del cambio de cantidad de movimiento. Si es el momento del sistema, entonces (ver )

es decir, el teorema es válido: la derivada temporal del impulso del sistema es igual al vector principal de todas las fuerzas externas.

Reemplazando el vector a través de su expresión donde es la masa del sistema, es la velocidad del centro de masa, se puede dar a la ecuación (4.1) una forma diferente:

Esta igualdad significa que el centro de masas del sistema se mueve como un punto material cuya masa es igual a la masa del sistema y al que se le aplica una fuerza que es geométricamente igual al vector principal de todas las fuerzas externas del sistema. El último enunciado se llama teorema sobre el movimiento del centro de masa (centro de inercia) del sistema.

Si entonces de (4.1) se deduce que el vector momento es constante en magnitud y dirección. Proyectándolo sobre el eje de coordenadas, obtenemos tres primeras integrales escalares de las ecuaciones diferenciales de la doble cadena del sistema:

Estas integrales se llaman integrales de cantidad de movimiento. Cuando la velocidad del centro de masa es constante, es decir, se mueve de manera uniforme y rectilínea.

Si la proyección del vector principal de fuerzas externas en cualquier eje, por ejemplo, en el eje, es igual a cero, entonces tenemos una primera integral, o si dos proyecciones del vector principal son iguales a cero, entonces hay dos integrales de la cantidad de movimiento.

2. Teorema sobre el cambio del momento cinético. Sea A un punto arbitrario en el espacio (móvil o estacionario), que no coincide necesariamente con ningún punto material particular del sistema durante todo el tiempo de movimiento. Denotamos su velocidad en un sistema fijo de coordenadas como El teorema sobre el cambio en el momento angular de un sistema material relativo al punto A tiene la forma

Si el punto A es fijo, entonces la igualdad (4.3) toma una forma más simple:

Esta igualdad expresa el teorema sobre el cambio del momento angular del sistema con respecto a un punto fijo: la derivada temporal del momento angular del sistema, calculada con respecto a algún punto fijo, es igual al momento principal de todas las fuerzas externas relativas a este punto.

Si entonces, según (4.4), el vector momento angular es constante en magnitud y dirección. Proyectándolo sobre el eje de coordenadas, obtenemos las primeras integrales escalares de las ecuaciones diferenciales del movimiento del sistema:

Estas integrales se denominan integrales del momento angular o integrales de las áreas.

Si el punto A coincide con el centro de masa del sistema, Entonces el primer término del lado derecho de la igualdad (4.3) se anula y el teorema sobre el cambio de momento angular tiene la misma forma (4.4) que en el caso de un punto fijo A. Nótese (ver 4 § 3) que en el caso bajo consideración el momento angular absoluto del sistema en el lado izquierdo de la igualdad (4.4) puede ser reemplazado por el momento angular igual del sistema en su movimiento relativo a el centro de masa.

Sea un eje constante o un eje de dirección constante que pasa por el centro de masa del sistema, y ​​sea el momento angular del sistema relativo a este eje. De (4.4) se sigue que

donde es el momento de las fuerzas externas con respecto al eje. Si durante todo el tiempo de movimiento tenemos la primera integral

En los trabajos de S. A. Chaplygin, se obtuvieron varias generalizaciones del teorema sobre el cambio en el momento angular, que luego se aplicaron para resolver una serie de problemas sobre el rodamiento de bolas. Los trabajos contienen generalizaciones adicionales del teorema sobre el cambio del momento kpnetológico y sus aplicaciones en problemas de la dinámica de un cuerpo rígido. Los principales resultados de estos trabajos están relacionados con el teorema sobre el cambio en el momento angular con respecto al móvil, pasando constantemente por algún punto móvil A. Sea un vector unitario dirigido a lo largo de este eje. Multiplicando escalarmente por ambos lados de la igualdad (4.3) y sumando el término a sus dos partes, obtenemos

Cuando se cumple la condición cinemática

la ecuación (4.5) se sigue de (4.7). Y si la condición (4.8) se cumple durante todo el tiempo de movimiento, entonces existe la primera integral (4.6).

Si las conexiones del sistema son ideales y permiten la rotación del sistema como un cuerpo rígido alrededor del eje y en el número de desplazamientos virtuales, entonces el momento principal de las reacciones alrededor del eje y es igual a cero, y luego el valor en el El lado derecho de la ecuación (4.5) es el momento principal de todas las fuerzas activas externas sobre el eje y . La igualdad a cero de este momento y la satisfacibilidad de la relación (4.8) serán en el caso bajo consideración condiciones suficientes para la existencia de la integral (4.6).

Si la dirección del eje y no cambia, entonces la condición (4.8) se puede escribir como

Esta igualdad significa que las proyecciones de la velocidad del centro de masa y la velocidad del punto A sobre el eje y sobre el plano perpendicular a este son paralelas. En el trabajo de S. A. Chaplygin, en lugar de (4.9), se requiere una condición menos general donde X es una constante arbitraria.

Tenga en cuenta que la condición (4.8) no depende de la elección de un punto en . De hecho, sea P un punto arbitrario en el eje. Después

y por lo tanto

En conclusión, notamos la interpretación geométrica de las ecuaciones de Resal (4.1) y (4.4): los vectores de velocidades absolutas de los extremos de los vectores y son iguales, respectivamente, al vector principal y al momento principal de todas las fuerzas externas relativas a el punto a

Ministerio de Educación y Ciencia de la Federación Rusa

Institución Educativa Presupuestaria del Estado Federal de Educación Profesional Superior

"Universidad Tecnológica Estatal de Kuban"

Mecánica teórica

Parte 2 dinámica

Aprobado por la Editorial y Editorial

consejo universitario como

guía de estudio

Krasnodar

CDU 531.1/3 (075)

Mecánica teórica. Parte 2. Dinámica: Libro de texto / L.I.Draiko; Kubán. estado technol.un-t. Krasnodar, 2011. 123 págs.

ISBN 5-230-06865-5

El material teórico se presenta de forma breve, se dan ejemplos de resolución de problemas, la mayoría de los cuales reflejan problemas técnicos reales, se presta atención a la elección de un método de solución racional.

Diseñado para licenciados en educación por correspondencia y a distancia en las áreas de construcción, transporte e ingeniería.

Pestaña. 1 figura 68 Bibliografía. 20 títulos

Editor científico Candidato a Ciencias Técnicas, Asoc. VF Melnikov

Revisores: Jefe del Departamento de Mecánica Teórica y Teoría de Mecanismos y Máquinas de la Universidad Agraria de Kuban prof. FM Kanarev; Profesor Asociado del Departamento de Mecánica Teórica de la Universidad Tecnológica Estatal de Kuban M.E. multikh

Publicado por decisión del Consejo Editorial y Editorial de la Universidad Tecnológica Estatal de Kuban.

Reedición

ISBN 5-230-06865-5 KubGTU 1998

Prefacio

Este libro de texto está destinado a estudiantes a tiempo parcial de las especialidades de construcción, transporte e ingeniería, pero puede ser utilizado cuando estudian la sección "Dinámica" del curso de mecánica teórica por estudiantes a tiempo parcial de otras especialidades, así como estudiantes a tiempo completo con Trabajo independiente.

El manual está compilado de acuerdo con el programa actual del curso de mecánica teórica, cubre todos los temas de la parte principal del curso. Cada sección contiene un breve material teórico, provisto de ilustraciones y pautas para su uso en la resolución de problemas. El manual analiza la solución de 30 tareas, reflejando los problemas reales de la tecnología y las tareas de control correspondientes para la solución independiente. Para cada tarea, se presenta un esquema de cálculo que ilustra claramente la solución. El diseño de la solución cumple con los requisitos para el diseño de exámenes de estudiantes a tiempo parcial.

El autor expresa su profundo agradecimiento a los docentes del Departamento de Mecánica Teórica y Teoría de Mecanismos y Máquinas de la Universidad Agraria de Kuban por su gran trabajo en la revisión del libro de texto, así como a los docentes del Departamento de Mecánica Teórica del Estado de Kuban Universidad Tecnológica por sus valiosos comentarios y consejos en la preparación del libro de texto para su publicación.

Todos los comentarios críticos y deseos serán aceptados por el autor con gratitud en el futuro.

Introducción

La dinámica es la rama más importante de la mecánica teórica. La mayoría de las tareas específicas que ocurren en la práctica de la ingeniería se relacionan con la dinámica. Utilizando las conclusiones de la estática y la cinemática, la dinámica establece las leyes generales del movimiento de los cuerpos materiales bajo la acción de fuerzas aplicadas.

El objeto material más simple es un punto material. Para un punto material, uno puede tomar un cuerpo material de cualquier forma, cuyas dimensiones en el problema bajo consideración pueden despreciarse. Un cuerpo de dimensiones finitas puede tomarse como un punto material si la diferencia en el movimiento de sus puntos no es significativa para un problema dado. Esto sucede cuando las dimensiones del cuerpo son pequeñas comparadas con las distancias que recorren los puntos del cuerpo. Cada partícula de un cuerpo rígido puede considerarse un punto material.

Las fuerzas aplicadas a un punto o un cuerpo material se evalúan en dinámica por su impacto dinámico, es decir, por cómo cambian las características del movimiento de los objetos materiales.

El movimiento de los objetos materiales a lo largo del tiempo tiene lugar en el espacio en relación con un cierto marco de referencia. En la mecánica clásica, basada en los axiomas de Newton, el espacio se considera tridimensional, sus propiedades no dependen de los objetos materiales que se mueven en él. La posición de un punto en dicho espacio está determinada por tres coordenadas. El tiempo no está conectado con el espacio y el movimiento de los objetos materiales. Se considera igual para todos los sistemas de referencia.

Las leyes de la dinámica describen el movimiento de los objetos materiales en relación con los ejes de coordenadas absolutas, convencionalmente tomados como inamovibles. El origen del sistema de coordenadas absolutas se toma en el centro del Sol, y los ejes se dirigen a estrellas distantes condicionalmente estacionarias. Al resolver muchos problemas técnicos, los ejes de coordenadas asociados con la Tierra pueden considerarse condicionalmente inamovibles.

Los parámetros del movimiento mecánico de los objetos materiales en la dinámica se establecen mediante deducciones matemáticas de las leyes básicas de la mecánica clásica.

Primera ley (ley de la inercia):

Un punto material mantiene un estado de reposo o movimiento uniforme y rectilíneo hasta que la acción de alguna fuerza lo saca de ese estado.

El movimiento uniforme y rectilíneo de un punto se llama movimiento de inercia. El reposo es un caso especial de movimiento por inercia, cuando la velocidad de un punto es cero.

Cualquier punto material tiene inercia, es decir, tiende a mantener un estado de reposo o movimiento rectilíneo uniforme. El marco de referencia en relación con el cual se satisface la ley de inercia se llama inercial, y el movimiento observado en relación con este marco se llama absoluto. Cualquier marco de referencia que realice un movimiento de traslación rectilíneo y uniforme en relación con el marco inercial también será un marco inercial.

La segunda ley (ley básica de la dinámica):

La aceleración de un punto material con respecto al marco de referencia inercial es proporcional a la fuerza aplicada al punto y coincide con la fuerza en la dirección:
.

De la ley básica de la dinámica se sigue que con una fuerza
aceleración
. La masa de un punto caracteriza el grado de resistencia de un punto a un cambio en su velocidad, es decir, es una medida de la inercia de un punto material.

Tercera ley (ley de acción y reacción):

Las fuerzas con las que dos cuerpos actúan entre sí son de igual magnitud y están dirigidas a lo largo de una línea recta en direcciones opuestas.

Las fuerzas llamadas acción y reacción se aplican a cuerpos diferentes y por lo tanto no forman un sistema equilibrado.

La cuarta ley (la ley de la independencia de la acción de las fuerzas):

Con la acción simultánea de varias fuerzas, la aceleración de un punto material es igual a la suma geométrica de las aceleraciones que tendría el punto bajo la acción de cada fuerza por separado:

, dónde
,
,…,
.

Muy a menudo, es posible aislar características importantes del movimiento de un sistema mecánico sin recurrir a la integración del sistema de ecuaciones diferenciales de movimiento. Esto se logra aplicando los teoremas generales de la dinámica.

5.1. Conceptos básicos y definiciones

Fuerzas externas e internas. Cualquier fuerza que actúe sobre un punto de un sistema mecánico es necesariamente una fuerza activa o una reacción de acoplamiento. El conjunto completo de fuerzas que actúan sobre los puntos del sistema se puede dividir en dos clases de manera diferente: en fuerzas externas y fuerzas internas (índices e e i - de las palabras latinas externus - externo e internus - interno). Las fuerzas externas se denominan fuerzas que actúan sobre puntos del sistema desde puntos y cuerpos que no forman parte del sistema en consideración. Las fuerzas de interacción entre puntos y cuerpos del sistema considerado se llaman internas.

Esta división depende de qué puntos y cuerpos materiales sean incluidos por el investigador en el sistema mecánico considerado. Si la composición del sistema se expande para incluir puntos y cuerpos adicionales, algunas fuerzas que eran externas para el sistema anterior pueden volverse internas para el sistema expandido.

Propiedades de las fuerzas internas. Dado que estas fuerzas son fuerzas de interacción entre partes del sistema, se incluyen en el sistema completo de fuerzas internas en "doses" organizados de acuerdo con el axioma de acción-reacción. Cada uno de esos "dos" de fuerzas

el vector principal y el momento principal con respecto a un centro arbitrario son iguales a cero. Dado que el sistema completo de fuerzas internas consta solo de "dos", entonces

1) el vector principal del sistema de fuerzas internas es igual a cero,

2) el momento principal del sistema de fuerzas internas relativo a un punto arbitrario es igual a cero.

La masa del sistema es la suma aritmética de las masas mk de todos los puntos y cuerpos que forman el sistema:

centro de gravedad(centro de inercia) de un sistema mecánico es un punto geométrico C, cuyo radio vector y coordenadas están determinados por las fórmulas

donde son los radios vectores y las coordenadas de los puntos que forman el sistema.

Para un cuerpo rígido en un campo gravitatorio uniforme, las posiciones del centro de masa y el centro de gravedad coinciden; en otros casos, estos son puntos geométricos diferentes.

Junto con el marco de referencia inercial, a menudo se considera simultáneamente un marco de referencia no inercial que avanza. Sus ejes de coordenadas (ejes de Koenig) se eligen de modo que el punto de referencia C coincida siempre con el centro de masas del sistema mecánico. De acuerdo con la definición, el centro de masa está fijo en los ejes de Koenig y está ubicado en el origen de coordenadas.

El momento de inercia del sistema. relativa al eje se llama cantidad escalar igual a la suma de los productos de las masas mk de todos los puntos del sistema por los cuadrados de sus distancias al eje:

Si el sistema mecánico es un cuerpo rígido, para encontrar 12, puedes usar la fórmula

donde es la densidad, el volumen ocupado por el cuerpo.