Cómo multiplicar un número entero por un decimal. Multiplicación de fracciones decimales: reglas, ejemplos, soluciones.

§ 107. Suma de fracciones decimales.

La suma de decimales se hace de la misma manera que la suma de números enteros. Veamos esto con ejemplos.

1) 0,132 + 2,354. Firmemos los términos uno debajo del otro.

Aquí, de la suma de 2 milésimas con 4 milésimas, se obtuvieron 6 milésimas;
de la suma de 3 centésimas con 5 centésimas, resultó 8 centésimas;
de sumar 1 décima con 3 décimas -4 décimas y
de sumar 0 enteros con 2 enteros - 2 enteros.

2) 5,065 + 7,83.

No hay milésimas en el segundo término, por lo que es importante no cometer errores al firmar los términos uno debajo del otro.

3) 1,2357 + 0,469 + 2,08 + 3,90701.

Aquí, al sumar milésimas, obtenemos 21 milésimas; escribimos 1 debajo de las milésimas y 2 sumado a las centésimas, por lo que en el lugar de las centésimas obtuvimos los siguientes términos: 2 + 3 + 6 + 8 + 0; en suma dan 19 centésimas, firmamos 9 bajo centésimas, y 1 se contaba como décimas, etc.

Así, al sumar fracciones decimales, se debe observar el siguiente orden: las fracciones se firman una debajo de la otra de modo que en todos los términos los mismos dígitos estén uno debajo del otro y todas las comas estén en la misma columna vertical; a la derecha de los lugares decimales de algunos términos, atribuyen, al menos mentalmente, tal número de ceros que todos los términos después del punto decimal tienen el mismo número de dígitos. Luego se realiza la suma por dígitos, comenzando por el lado derecho, y en la cantidad resultante se coloca una coma en la misma columna vertical que en estos términos.

§ 108. Resta de fracciones decimales.

La resta de decimales se hace de la misma manera que la resta de números enteros. Mostremos esto con ejemplos.

1) 9,87 - 7,32. Firmemos el sustraendo debajo del minuendo para que las unidades de un mismo dígito queden una debajo de la otra:

2) 16.29 - 4.75. Firmemos el sustraendo debajo del minuendo, como en el primer ejemplo:

Para restar décimas, había que tomar una unidad entera de 6 y dividirla en décimas.

3) 14.0213-5.350712. Firmemos el sustraendo debajo del minuendo:

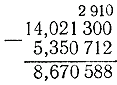
La resta se realizó de la siguiente manera: como no podemos restar 2 millonésimas de 0, debemos referirnos al dígito más cercano a la izquierda, es decir, a las cienmilésimas, pero también hay cero en lugar de las cienmilésimas, así que tomamos 1 diezmilésima de 3 diezmilésimas y lo dividimos en cienmilésimas, obtenemos 10 cienmilésimas, de las cuales 9 cienmilésimas quedan en la categoría de cienmilésimas, y 1 cienmilésima se tritura en millonésimas, obtenemos 10 millonésimas. Así, en los últimos tres dígitos, obtuvimos: millonésimas 10, cienmilésimas 9, diezmilésimas 2. Para mayor claridad y comodidad (no olvidar), estos números se escriben encima de los dígitos fraccionarios correspondientes de la reducción. Ahora podemos empezar a restar. Restamos 2 millonésimas de 10 millonésimas, obtenemos 8 millonésimas; restamos 1 cienmilésima de 9 cienmilésimas, obtenemos 8 cienmilésimas, etc.

Así, al restar fracciones decimales, se observa el siguiente orden: lo restado se firma debajo de lo reducido de modo que los mismos dígitos queden uno debajo del otro y todas las comas estén en la misma columna vertical; a la derecha, atribuyen, al menos mentalmente, en la reducida o restada tantos ceros para que tengan el mismo número de dígitos, luego restan por dígitos, comenzando por el lado derecho, y en la diferencia resultante ponen una coma en el misma columna vertical en la que se reduce y resta.

§ 109. Multiplicación de fracciones decimales.

Considere algunos ejemplos de multiplicación de fracciones decimales.

Para encontrar el producto de estos números, podemos razonar de la siguiente manera: si el factor se multiplica por 10, entonces ambos factores serán números enteros y luego podemos multiplicarlos de acuerdo con las reglas para multiplicar números enteros. Pero sabemos que cuando uno de los factores aumenta varias veces, el producto aumenta en la misma cantidad. Esto significa que el número que resulta de multiplicar factores enteros, es decir, 28 por 23, es 10 veces mayor que el producto real, y para obtener el producto real, debe reducir el producto encontrado en 10 veces. Por lo tanto, aquí debe realizar una multiplicación por 10 una vez y una división por 10 una vez, pero la multiplicación y la división por 10 se realizan moviendo la coma hacia la derecha y hacia la izquierda un signo. Por lo tanto, debe hacer esto: en el multiplicador, mueva la coma hacia la derecha en un signo, de esto será igual a 23, luego debe multiplicar los números enteros resultantes:

Este producto es 10 veces más grande que el verdadero. Por lo tanto, debe reducirse 10 veces, para lo cual movemos la coma un carácter hacia la izquierda. Así, obtenemos

28 2,3 = 64,4.

Para fines de verificación, puede escribir una fracción decimal con un denominador y realizar una acción de acuerdo con la regla para multiplicar fracciones ordinarias, es decir

2) 12,27 0,021.

La diferencia entre este ejemplo y el anterior es que aquí ambos factores están representados por fracciones decimales. Pero aquí, en el proceso de multiplicación, no prestaremos atención a las comas, es decir, aumentaremos temporalmente el multiplicador 100 veces y el multiplicador 1000 veces, lo que aumentará el producto 100 000 veces. Así, multiplicando 1227 por 21, obtenemos:

1 227 21 = 25 767.

Teniendo en cuenta que el producto resultante es 100.000 veces mayor que el verdadero, ahora debemos reducirlo 100.000 veces colocándole correctamente una coma, entonces obtenemos:

32,27 0,021 = 0,25767.

Vamos a revisar:

Así, para multiplicar dos fracciones decimales basta, sin prestar atención a las comas, con multiplicarlas por enteros y en el producto separar con una coma del lado derecho tantos decimales como había en el multiplicando y en el factor juntos.

En el último ejemplo, el resultado es un producto con cinco decimales. Si no se requiere una mayor precisión, se realiza el redondeo de la fracción decimal. Al redondear, debe usar la misma regla que se indicó para los números enteros.

§ 110. Multiplicación mediante tablas.

La multiplicación de decimales a veces se puede hacer usando tablas. Para este propósito, puede, por ejemplo, usar esas tablas de multiplicar de números de dos dígitos, cuya descripción se proporcionó anteriormente.

1) Multiplica 53 por 1,5.

Multiplicaremos 53 por 15. En la tabla, este producto es igual a 795. Encontramos el producto de 53 por 15, pero nuestro segundo factor fue 10 veces menor, lo que significa que el producto debe reducirse 10 veces, es decir

53 1,5 = 79,5.

2) Multiplica 5,3 por 4,7.

Primero, busquemos el producto de 53 por 47 en la tabla, será 2491. Pero como aumentamos el multiplicando y el multiplicador en un total de 100 veces, entonces el producto resultante es 100 veces mayor de lo que debería ser; entonces tenemos que reducir este producto por un factor de 100:

5,3 4,7 = 24,91.

3) Multiplica 0,53 por 7,4.

Primero encontramos en la tabla el producto de 53 por 74; esto será 3922. Pero como hemos aumentado el multiplicador 100 veces, y el multiplicador 10 veces, el producto ha aumentado 1000 veces; entonces ahora tenemos que reducirlo por un factor de 1,000:

0,53 7,4 = 3,922.

§ 111. División de decimales.

Veremos la división decimal en este orden:

1. División de una fracción decimal por un número entero,

1. División de una fracción decimal por un número entero.

1) Divide 2,46 entre 2.

Dividimos por 2 primeros enteros, luego décimas y finalmente centésimas.

2) Divide 32,46 entre 3.

32,46: 3 = 10,82.

Dividimos 3 decenas por 3, luego comenzamos a dividir 2 unidades por 3; como el número de unidades del dividendo (2) es menor que el divisor (3), tuvimos que poner 0 en el cociente; además, al resto demolimos 4 décimas y dividimos 24 décimas por 3; recibió en privado 8 décimas y finalmente dividió 6 centésimas.

3) Divide 1.2345 entre 5.

1,2345: 5 = 0,2469.

Aquí, en el cociente en primer lugar, resultaron cero números enteros, ya que un número entero no es divisible por 5.

4) Divide 13,58 entre 4.

La peculiaridad de este ejemplo es que cuando sacamos 9 centésimas en privado, entonces se encontró un resto igual a 2 centésimas, dividimos este resto en milésimas, obtuvimos 20 milésimas y llevamos la división al final.

Regla. La división de una fracción decimal por un número entero se realiza de la misma forma que la división de números enteros, y los residuos resultantes se convierten en fracciones decimales, cada vez más pequeñas; la división continúa hasta que el resto es cero.

2. División de una fracción decimal por una fracción decimal.

1) Divide 2,46 entre 0,2.

Ya sabemos cómo dividir una fracción decimal por un número entero. Pensemos si este nuevo caso de división también se puede reducir al anterior. En un momento, consideramos una propiedad notable del cociente, que consiste en el hecho de que permanece sin cambios mientras aumenta o disminuye el dividendo y el divisor por el mismo número de veces. Fácilmente realizaríamos la división de los números que se nos ofrecen si el divisor fuera un número entero. Para ello, basta con aumentarlo 10 veces, y para obtener el cociente correcto es necesario aumentar el dividendo la misma cantidad de veces, es decir, 10 veces. Entonces la división de estos números será reemplazada por la división de tales números:

y no hay necesidad de hacer ninguna enmienda en privado.

Hagamos esta división:

Entonces 2.46: 0.2 = 12.3.

2) Divide 1,25 entre 1,6.

Aumentamos el divisor (1.6) en 10 veces; para que el cociente no cambie, aumentamos el dividendo 10 veces; 12 enteros no son divisibles por 16, entonces escribimos en el cociente 0 y dividimos 125 décimas entre 16, obtenemos 7 décimas en el cociente y el resto es 13. Dividimos 13 décimas en centésimas asignando cero y dividimos 130 centésimas entre 16, etc. Preste atención a lo siguiente:

a) cuando no se obtienen números enteros en el cociente, entonces se escriben ceros en su lugar;

b) cuando después de restar la cifra del dividendo al resto se obtiene un número que no es divisible por el divisor, entonces se escribe cero en el cociente;

c) cuando, después de haber quitado el último dígito del dividendo, la división no termina, entonces, asignando ceros a los restos, continúa la división;

d) si el dividendo es un número entero, entonces al dividirlo por una fracción decimal, su aumento se realiza asignándole ceros.

Por lo tanto, para dividir un número por una fracción decimal, debe descartar una coma en el divisor y luego aumentar el dividendo tantas veces como aumentó el divisor cuando se eliminó la coma, y ​​luego realizar la división de acuerdo con la regla de dividir la fracción decimal por un número entero.

§ 112. Cociente aproximado.

En el párrafo anterior, consideramos la división de fracciones decimales, y en todos los ejemplos que resolvimos, la división se llevó al final, es decir, se obtuvo un cociente exacto. Sin embargo, en la mayoría de los casos no se puede obtener el cociente exacto, por mucho que extendamos la división. Aquí hay uno de esos casos: divide 53 entre 101.

Ya hemos recibido cinco dígitos en el cociente, pero la división aún no ha terminado y no hay esperanza de que termine, ya que los números que hemos encontrado antes comienzan a aparecer en el resto. Los números también se repetirán en el cociente: obviamente, después del número 7, aparecerá el número 5, luego el 2, y así hasta el infinito. En tales casos, la división se interrumpe y se limita a los primeros dígitos del cociente. Este privado se llama aproximado. Cómo realizar la división en este caso, lo mostraremos con ejemplos.

Que se requiera dividir 25 por 3. Es obvio que el cociente exacto, expresado como una fracción entera o decimal, no se puede obtener de tal división. Por lo tanto, buscaremos un cociente aproximado:

25: 3 = 8 y resto 1

El cociente aproximado es 8; es, por supuesto, menor que el cociente exacto, porque queda un resto de 1. Para obtener el cociente exacto, debe agregar al cociente aproximado encontrado, es decir, a 8, la fracción que resulta de dividir el resto , igual a 1, por 3; será una fracción 1/3. Esto significa que el cociente exacto se expresará como un número mixto 8 1/3. Como 1/3 es una fracción propia, es decir, una fracción, menos que uno, entonces, descartándolo, suponemos error, cual menos que uno. privado 8 voluntad cociente aproximado hasta uno con desventaja. Si tomamos 9 en lugar de 8, también permitimos un error menor que uno, ya que no sumaremos una unidad entera, sino 2/3. Un testamento tan privado cociente aproximado hasta uno con exceso.

Tomemos otro ejemplo ahora. Que sea necesario dividir 27 entre 8. Como aquí no obtendremos un cociente exacto expresado como un número entero, buscaremos un cociente aproximado:

27: 8 = 3 y resto 3.

Aquí el error es 3/8, es menor que uno, lo que significa que el cociente aproximado (3) se encuentra hasta uno con un inconveniente. Continuamos la división: partimos el resto de 3 en décimas, nos salen 30 décimas; Vamos a dividirlos por 8.

Conseguimos en privado en el acto décimas 3 y en el resto b décimas. Si nos limitamos al número 3.3 en particular y descartamos el resto 6, permitiremos un error de menos de una décima. ¿Por qué? Porque el cociente exacto se obtendría cuando sumamos a 3,3 el resultado de dividir 6 décimas entre 8; de esta división sería 6/80, que es menos de una décima. (¡Compruebe!) Por lo tanto, si nos limitamos a las décimas en el cociente, entonces podemos decir que hemos encontrado el cociente exacto a una décima(con desventaja).

Continuemos la división para encontrar un lugar decimal más. Para hacer esto, dividimos 6 décimas en centésimas y obtenemos 60 centésimas; Vamos a dividirlos por 8.

En privado en tercer lugar resultó 7 y en el resto 4 centésimas; si los descartamos, entonces permitimos un error de menos de una centésima, porque 4 centésimas divididas por 8 es menos de una centésima. En tales casos, se dice que se encuentra el cociente. precisión a la centésima(con desventaja).

En el ejemplo que ahora estamos considerando, puedes obtener el cociente exacto, expresado como una fracción decimal. Para ello, basta con dividir el último resto, 4 centésimas, en milésimas y dividir por 8.

Sin embargo, en la gran mayoría de los casos es imposible obtener un cociente exacto y hay que limitarse a sus valores aproximados. Ahora consideraremos un ejemplo de este tipo:

40: 7 = 5,71428571...

Los puntos al final del número indican que la división no está completa, es decir, la igualdad es aproximada. Por lo general, la igualdad aproximada se escribe así:

40: 7 = 5,71428571.

Tomamos el cociente con ocho decimales. Pero si no se requiere una precisión tan grande, uno puede limitarse a la parte entera del cociente, es decir, el número 5 (más precisamente, 6); para mayor precisión se podrían tomar en cuenta las décimas y tomar el cociente igual a 5.7; si por alguna razón esta precisión es insuficiente, entonces podemos detenernos en centésimas y tomar 5.71, etc. Escribamos los cocientes individuales y nómbrelos.

El primer cociente aproximado hasta uno 6.

El segundo » » » a la décima 5.7.

Tercera » » » hasta la centésima 5.71.

Cuarto » » » hasta la milésima parte de 5.714.

Por lo tanto, para encontrar un cociente aproximado hasta algo, por ejemplo, el 3er lugar decimal (es decir, hasta una milésima), la división se detiene tan pronto como se encuentra este signo. En este caso, se debe recordar la regla establecida en el § 40.

§ 113. Los problemas más simples de interés.

Después de estudiar fracciones decimales, resolveremos algunos problemas de porcentajes más.

Estos problemas son similares a los que resolvimos en el departamento de fracciones ordinarias; pero ahora escribiremos las centésimas en forma de fracciones decimales, es decir, sin un denominador designado explícitamente.

En primer lugar, debe poder cambiar fácilmente de una fracción ordinaria a una fracción decimal con un denominador de 100. Para hacer esto, debe dividir el numerador por el denominador:

La siguiente tabla muestra cómo un número con un símbolo % (porcentaje) se reemplaza por un decimal con un denominador de 100:

Consideremos ahora algunos problemas.

1. Encontrar porcentajes de un número dado.

Tarea 1. Solo 1.600 personas viven en un pueblo. El número de niños en edad escolar es el 25% de la población total. ¿Cuántos niños en edad escolar hay en este pueblo?

En este problema, necesitas encontrar el 25%, o 0,25, de 1600. El problema se resuelve multiplicando:

1.600 0,25 = 400 (niños).

Por lo tanto, el 25% de 1600 es 400.

Para una clara comprensión de esta tarea, es útil recordar que por cada cien habitantes hay 25 niños en edad escolar. Por lo tanto, para encontrar el número de todos los niños en edad escolar, primero puede averiguar cuántas centenas hay en el número 1600 (16) y luego multiplicar 25 por el número de centenas (25 x 16 = 400). De esta manera se puede comprobar la validez de la solución.

Tarea 2. Las cajas de ahorro dan a los depositantes el 2% de los ingresos anuales. ¿Cuánto ingreso por año recibirá un depositante que haya depositado: a) 200 rublos? b) 500 rublos? c) 750 rublos? d) 1000 rublos?

En los cuatro casos, para resolver el problema será necesario calcular 0,02 de las cantidades indicadas, es decir, cada uno de estos números habrá que multiplicarlos por 0,02. Vamos a hacerlo:

a) 200 0,02 = 4 (rublos),

b) 500 0,02 = 10 (rublos),

c) 750 0,02 = 15 (rublos),

d) 1.000 0,02 = 20 (rublos).

Cada uno de estos casos puede ser verificado por las siguientes consideraciones. Las Cajas de Ahorros entregan a los depositantes el 2% de los ingresos, es decir, el 0,02 de la cantidad depositada en ahorros. Si la cantidad fuera de 100 rublos, entonces 0,02 serían 2 rublos. Esto significa que cada cien aporta al depositante 2 rublos. ingreso. Por lo tanto, en cada uno de los casos considerados, es suficiente averiguar cuántos cientos hay en un número dado y multiplicar 2 rublos por este número de cientos. En el ejemplo a) centenas de 2, entonces

2 2 \u003d 4 (rublos).

En el ejemplo d) las centenas son 10, lo que significa

2 10 \u003d 20 (rublos).

2. Encontrar un número por su porcentaje.

Tarea 1. En la primavera, la escuela graduó a 54 estudiantes, lo que representa el 6% del número total de estudiantes. ¿Cuántos estudiantes había en la escuela durante el último año académico?

Aclaremos primero el significado de este problema. La escuela graduó a 54 alumnos, lo que representa el 6% del total de alumnos, es decir, 6 centésimas (0,06) de todos los alumnos de la escuela. Esto quiere decir que conocemos la parte de los alumnos expresada por el número (54) y la fracción (0.06), ya partir de esta fracción debemos hallar el número entero. Por lo tanto, tenemos ante nosotros un problema ordinario de encontrar un número por su fracción (§ 90 p. 6). Los problemas de este tipo se resuelven por división:

Esto significa que había 900 estudiantes en la escuela.

Es útil verificar tales problemas resolviendo el problema inverso, es decir, después de resolver el problema, debe, al menos en su mente, resolver el problema del primer tipo (encontrar el porcentaje de un número dado): tome el número encontrado ( 900) tal como se da y encuentre el porcentaje indicado en el problema resuelto a partir de él, a saber:

900 0,06 = 54.

Tarea 2. La familia gasta 780 rublos en comida durante el mes, lo que representa el 65% de los ingresos mensuales del padre. Determine su ingreso mensual.

Esta tarea tiene el mismo significado que la anterior. Da parte de las ganancias mensuales, expresadas en rublos (780 rublos), e indica que esta parte es el 65%, o 0,65, de las ganancias totales. Y lo deseado es la totalidad de las ganancias:

780: 0,65 = 1 200.

Por lo tanto, las ganancias deseadas son 1200 rublos.

3. Encontrar el porcentaje de números.

Tarea 1. La biblioteca escolar tiene un total de 6.000 libros. Entre ellos hay 1.200 libros de matemáticas. ¿Qué porcentaje de libros de matemáticas componen el número total de libros en la biblioteca?

Ya hemos considerado (§97) este tipo de problema y llegamos a la conclusión de que para calcular el porcentaje de dos números, debe encontrar la proporción de estos números y multiplicarla por 100.

En nuestra tarea, necesitamos encontrar el porcentaje de los números 1200 y 6000.

Primero encontramos su proporción y luego la multiplicamos por 100:

Por lo tanto, el porcentaje de los números 1200 y 6000 es 20. En otras palabras, los libros de matemáticas representan el 20% del número total de todos los libros.

Para comprobarlo, resolvemos el problema inverso: hallar el 20% de 6000:

6 000 0,2 = 1 200.

Tarea 2. La planta debe recibir 200 toneladas de carbón. Ya se han entregado 80 toneladas ¿Qué porcentaje de carbón se ha entregado a la planta?

Este problema pregunta qué porcentaje es un número (80) de otro (200). La relación de estos números será 80/200. Multipliquemos por 100:

Esto significa que se ha entregado el 40% del carbón.

multiplicación de decimales tiene lugar en tres etapas.

Los decimales se escriben en una columna y se multiplican como números ordinarios.

Contamos el número de lugares decimales para el primer decimal y el segundo. Agregamos su número.

En el resultado obtenido, contamos de derecha a izquierda tantos dígitos como resultaron en el párrafo anterior y ponemos una coma.

como multiplicar decimales

Escribimos fracciones decimales en una columna y las multiplicamos como números naturales, ignorando las comas. Es decir, consideramos 3,11 como 311 y 0,01 como 1.

Recibido 311 . Ahora contamos el número de signos (dígitos) después del punto decimal para ambas fracciones. El primer decimal tiene dos dígitos y el segundo tiene dos. Número total de dígitos después de las comas:

Contamos de derecha a izquierda 4 caracteres (números) del número resultante. Hay menos dígitos en el resultado de los que necesita separar con una coma. En ese caso, necesita izquierda asignar el número faltante de ceros.

Nos falta un dígito, así que atribuimos un cero a la izquierda.

Al multiplicar cualquier fracción decimal el 10; 100; 1000 etc el punto decimal se mueve hacia la derecha tantos dígitos como ceros hay después del uno.

70,1 10 = 701

0,023 100 = 2,3

5.6 1000 = 5600

Para multiplicar un decimal por 0,1; 0,01; 0.001, etc., es necesario mover la coma hacia la izquierda en esta fracción tantos dígitos como ceros hay delante de la unidad.

¡Contamos cero enteros!

• 12 0,1 = 1,2
• 0,05 0,1 = 0,005
• 1,256 0,01 = 0,012 56

Para entender cómo multiplicar decimales, veamos ejemplos específicos.

Regla de multiplicación decimal

1) Multiplicamos ignorando la coma.

2) Como resultado, separamos tantos dígitos después de la coma como hay después de las comas en ambos factores juntos.

Encuentra el producto de decimales:

Para multiplicar decimales, multiplicamos sin prestar atención a las comas. Es decir, no multiplicamos 6,8 y 3,4, sino 68 y 34. Como resultado, separamos tantos dígitos después del punto decimal como hay después de las comas en ambos factores juntos. En el primer multiplicador hay un dígito después del punto decimal, en el segundo también hay uno. En total, separamos dos dígitos después del punto decimal, por lo que obtuvimos la respuesta final: 6.8∙3.4=23.12.

Multiplicar decimales sin tener en cuenta la coma. Es decir, de hecho, en lugar de multiplicar 36.85 por 1.14, multiplicamos 3685 por 14. Obtenemos 51590. Ahora en este resultado necesitamos separar tantos dígitos con una coma como haya en ambos factores juntos. El primer número tiene dos dígitos después del punto decimal, el segundo tiene uno. En total, separamos tres dígitos con una coma. Como hay un cero al final de la entrada después del punto decimal, no lo escribimos como respuesta: 36,85∙1,4=51,59.

Para multiplicar estos decimales, multiplicamos los números sin prestar atención a las comas. Es decir, multiplicamos los números naturales 2315 y 7. Obtenemos 16205. En este número se deben separar cuatro dígitos después del punto decimal, tantos como haya en ambos factores juntos (dos en cada uno). Respuesta final: 23,15∙0,07=1,6205.

La multiplicación de una fracción decimal por un número natural se hace de la misma manera. Multiplicamos los números sin prestar atención a la coma, es decir, multiplicamos 75 por 16. En el resultado obtenido, después de la coma debe haber tantos signos como en ambos factores juntos: uno. Por lo tanto, 75∙1.6=120.0=120.

Comenzamos la multiplicación de fracciones decimales multiplicando números naturales, ya que no prestamos atención a las comas. Después de eso, separamos tantos dígitos después de la coma como haya en ambos factores juntos. El primer número tiene dos lugares decimales, y el segundo tiene dos lugares decimales. En total, como resultado, debe haber cuatro dígitos después del punto decimal: 4,72∙5,04=23,7888.

Y un par de ejemplos más para multiplicar fracciones decimales:

www.for6cl.uznateshe.ru

Multiplicación de fracciones decimales, reglas, ejemplos, soluciones.

Pasamos al estudio de la siguiente acción con fracciones decimales, ahora consideraremos de manera integral multiplicando decimales. Primero, analicemos los principios generales de la multiplicación de fracciones decimales. Después de eso, pasemos a multiplicar una fracción decimal por una fracción decimal, muestre cómo se realiza la multiplicación de fracciones decimales por una columna, considere las soluciones de los ejemplos. A continuación, analizaremos la multiplicación de fracciones decimales por números naturales, en concreto por 10, 100, etc. En conclusión, hablemos de multiplicar fracciones decimales por fracciones ordinarias y números mixtos.

Digamos de inmediato que en este artículo solo hablaremos de multiplicar fracciones decimales positivas (ver números positivos y negativos). Los casos restantes se analizan en los artículos multiplicación de números racionales y multiplicacion de numeros reales.

Navegación de página.

Principios generales para multiplicar decimales

Analicemos los principios generales que deben seguirse al realizar la multiplicación con fracciones decimales.

Dado que los decimales finales y las fracciones periódicas infinitas son la forma decimal de las fracciones comunes, multiplicar dichos decimales es esencialmente multiplicar fracciones comunes. En otras palabras, multiplicacion de decimales finales, multiplicación de fracciones decimales finales y periódicas, tanto como multiplicar decimales periodicos se reduce a multiplicar fracciones ordinarias después de convertir fracciones decimales en fracciones ordinarias.

Considere ejemplos de la aplicación del principio expresado de multiplicar fracciones decimales.

Realiza la multiplicación de decimales 1,5 y 0,75.

Sustituyamos las fracciones decimales multiplicadas por las correspondientes fracciones ordinarias. Como 1,5=15/10 y 0,75=75/100, entonces. Puede reducir la fracción y luego seleccionar la parte entera de la fracción impropia, y es más conveniente escribir la fracción ordinaria resultante 1 125/1 000 como una fracción decimal 1.125.

Cabe señalar que es conveniente multiplicar las fracciones decimales finales en una columna, hablaremos de este método de multiplicación de fracciones decimales en el siguiente párrafo.

Considere un ejemplo de multiplicación de fracciones decimales periódicas.

Calcule el producto de los decimales periódicos 0,(3) y 2,(36) .

Convirtamos fracciones decimales periódicas a fracciones ordinarias:

Después. Puede convertir la fracción ordinaria resultante en una fracción decimal:


Si hay infinitas fracciones no periódicas entre las fracciones decimales multiplicadas, entonces todas las fracciones multiplicadas, incluidas las finitas y periódicas, deben redondearse a un cierto dígito (ver números de redondeo), y luego realizar la multiplicación de las fracciones decimales finales obtenidas después del redondeo.

Multiplica los decimales 5.382… y 0.2.

Primero, redondeamos una fracción decimal infinita no periódica, el redondeo se puede hacer a las centésimas, tenemos 5.382 ... ≈5.38. La fracción decimal final 0.2 no necesita ser redondeada a centésimas. Así, 5.382… 0.2≈5.38 0.2. Queda por calcular el producto de fracciones decimales finales: 5.38 0.2 \u003d 538 / 100 2 / 10 \u003d 1,076/1,000 \u003d 1.076.

Multiplicación de fracciones decimales por una columna

La multiplicación de fracciones decimales finitas se puede realizar por una columna, similar a la multiplicación por una columna de números naturales.

vamos a formular regla de multiplicación para fracciones decimales. Para multiplicar fracciones decimales por una columna, necesitas:

• ignorando las comas, realice la multiplicación de acuerdo con todas las reglas de multiplicación por una columna de números naturales;
• en el número resultante, separe tantos dígitos a la derecha con un punto decimal como decimales haya en ambos factores juntos, y si no hay suficientes dígitos en el producto, entonces se debe agregar a la izquierda el número requerido de ceros.

Considere ejemplos de multiplicación de fracciones decimales por una columna.

Multiplica los decimales 63,37 y 0,12.

Realicemos la multiplicación de fracciones decimales por una columna. Primero, multiplicamos los números, ignorando las comas:


Queda por poner una coma en el producto resultante. Necesita separar 4 dígitos a la derecha, ya que hay cuatro lugares decimales en los factores (dos en la fracción 3.37 y dos en la fracción 0.12). Hay suficientes números allí, así que no tienes que agregar ceros a la izquierda. Terminemos el registro:


Como resultado, tenemos 3,37 0,12 = 7,6044.

Calcula el producto de los decimales 3,2601 y 0,0254.

Habiendo realizado la multiplicación por una columna sin tener en cuenta las comas, obtenemos la siguiente imagen:


Ahora, en el producto, debe separar 8 dígitos a la derecha con una coma, ya que el número total de lugares decimales de las fracciones multiplicadas es ocho. Pero solo hay 7 dígitos en el producto, por lo tanto, debe asignar tantos ceros a la izquierda para que 8 dígitos puedan separarse con una coma. En nuestro caso, necesitamos asignar dos ceros:


Esto completa la multiplicación de fracciones decimales por una columna.

Multiplicar decimales por 0,1, 0,01, etc.

Muy a menudo tienes que multiplicar decimales por 0,1, 0,01, etc. Por lo tanto, es recomendable formular una regla para multiplicar una fracción decimal por estos números, que se deriva de los principios de la multiplicación de fracciones decimales discutidos anteriormente.

Asi que, multiplicar un decimal dado por 0,1, 0,01, 0,001, etc. da una fracción, que se obtiene a partir de la original, si en su entrada la coma se mueve hacia la izquierda 1, 2, 3 y así sucesivamente dígitos, respectivamente, y si no hay suficientes dígitos para mover la coma, entonces necesita agregar el número requerido de ceros a la izquierda.

Por ejemplo, para multiplicar la fracción decimal 54,34 por 0,1, debe mover el punto decimal 1 dígito hacia la izquierda en la fracción 54,34 y obtendrá la fracción 5,434, es decir, 54,34 0,1 \u003d 5,434. Tomemos otro ejemplo. Multiplica la fracción decimal 9,3 por 0,0001. Para hacer esto, necesitamos mover la coma 4 dígitos hacia la izquierda en la fracción decimal multiplicada 9.3, pero el registro de la fracción 9.3 no contiene tal número de caracteres. Por lo tanto, debemos asignar tantos ceros en el registro de la fracción 9.3 a la izquierda para que podamos transferir fácilmente la coma a 4 dígitos, tenemos 9.3 0.0001 \u003d 0.00093.

Tenga en cuenta que la regla anunciada para multiplicar una fracción decimal por 0,1, 0,01, ... también es válida para fracciones decimales infinitas. Por ejemplo, 0,(18) 0,01=0,00(18) o 93,938… 0,1=9,3938… .

Multiplicar un decimal por un número natural

En su centro multiplicar decimales por numeros naturales no es diferente de multiplicar un decimal por un decimal.

Es más conveniente multiplicar una fracción decimal finita por un número natural por una columna, mientras que debe seguir las reglas para multiplicar por una columna de fracciones decimales discutidas en uno de los párrafos anteriores.

Calcular el producto 15 2.27 .

Realicemos la multiplicación de un número natural por una fracción decimal en una columna:


Al multiplicar una fracción decimal periódica por un número natural, la fracción periódica debe reemplazarse con una fracción ordinaria.

Multiplica la fracción decimal 0,(42) por el número natural 22.

Primero, vamos a convertir el decimal periódico a una fracción común:

Ahora hagamos la multiplicación: . Este resultado decimal es 9,(3) .

Y al multiplicar una fracción decimal no periódica infinita por un número natural, primero debes redondear.

Haz la multiplicación 4 2.145….

Redondeando a centésimas la fracción decimal infinita original, llegaremos a la multiplicación de un número natural y una fracción decimal final. Tenemos 4 2.145…≈4 2.15=8.60.

Multiplicar un decimal por 10, 100,...

Muy a menudo hay que multiplicar fracciones decimales por 10, 100, ... Por lo tanto, es recomendable detenerse en estos casos en detalle.

vamos a voz Regla para multiplicar un decimal por 10, 100, 1000, etc. Al multiplicar una fracción decimal por 10, 100, ... en su entrada, debe mover la coma a la derecha en 1, 2, 3, ... dígitos, respectivamente, y descartar los ceros adicionales a la izquierda; si no hay suficientes dígitos en el registro de la fracción multiplicada para transferir la coma, debe agregar la cantidad requerida de ceros a la derecha.

Multiplica el decimal 0.0783 por 100.

Transfiramos la fracción 0.0783 dos dígitos a la derecha al registro y obtenemos 007.83. Dejando caer dos ceros a la izquierda, obtenemos la fracción decimal 7.38. Por lo tanto, 0,0783 100 = 7,83.

Multiplica la fracción decimal 0,02 por 10.000.

Para multiplicar 0.02 por 10,000 necesitamos mover la coma 4 dígitos a la derecha. Evidentemente, en el registro de la fracción 0,02 no hay suficientes dígitos para pasar la coma a 4 dígitos, por lo que añadiremos unos ceros a la derecha para que se pueda pasar la coma. En nuestro ejemplo basta con sumar tres ceros, tenemos 0,02000. Después de mover la coma, obtenemos la entrada 00200.0. Quitando los ceros de la izquierda, tenemos el número 200,0, que es igual al número natural 200, es el resultado de multiplicar la fracción decimal 0,02 por 10.000.

La regla indicada también es válida para multiplicar fracciones decimales infinitas por 10, 100, ... Al multiplicar fracciones decimales periódicas, debe tener cuidado con el período de la fracción que es el resultado de la multiplicación.

Multiplica el decimal periódico 5.32(672) por 1000 .

Antes de la multiplicación, escribimos la fracción decimal periódica como 5.32672672672..., esto nos permitirá evitar errores. Ahora vamos a mover la coma a la derecha 3 dígitos, tenemos 5 326.726726... . Así, después de la multiplicación, se obtiene una fracción decimal periódica 5 326, (726) .

5.32(672) 1000=5326,(726) .

Al multiplicar infinitas fracciones no periódicas por 10, 100, ..., primero debe redondear la fracción infinita a un dígito determinado y luego realizar la multiplicación.

Multiplicar un decimal por una fracción común o un número mixto

Para multiplicar una fracción decimal finita o una fracción decimal periódica infinita por una fracción ordinaria o un número mixto, debe representar la fracción decimal como una fracción ordinaria y luego realizar la multiplicación.

Multiplica la fracción decimal 0,4 por el número mixto.

Desde 0.4=4/10=2/5 y luego. El número resultante se puede escribir como una fracción decimal periódica 1.5(3) .

Al multiplicar una fracción decimal no periódica infinita por una fracción común o un número mixto, la fracción común o número mixto debe reemplazarse por una fracción decimal, luego redondear las fracciones multiplicadas y finalizar el cálculo.

Desde 2/3 \u003d 0.6666 ..., entonces. Después de redondear las fracciones multiplicadas a milésimas, llegamos al producto de dos fracciones decimales finales 3,568 y 0,667. Hagamos la multiplicación en una columna:


El resultado obtenido debe redondearse a las milésimas, ya que las fracciones multiplicadas fueron tomadas con una precisión de milésimas, tenemos 2.379856≈2.380.

www.cleverstudents.ru

29. Multiplicación de fracciones decimales. Normas




Hallar el area de un rectangulo de lados iguales
1,4 dm y 0,3 dm. Convertir decímetros a centímetros:

1,4 dm = 14 cm; 0,3 dm = 3 cm.

Ahora calculemos el área en centímetros.

S \u003d 14 3 \u003d 42 cm 2.

Convertir centímetros cuadrados en cuadrados
decímetros:

d m 2 \u003d 0,42 d m 2.

Por lo tanto, S \u003d 1,4 dm 0,3 dm \u003d 0,42 dm 2.

La multiplicación de dos decimales se hace así:
1) los números se multiplican sin tener en cuenta las comas.
2) la coma en el producto se coloca para separar a la derecha
tantos signos como separados en ambos factores
tomados en conjunto. Por ejemplo:

1,1 0,2 = 0,22 ; 1,1 1,1 = 1,21 ; 2,2 0,1 = 0,22 .

Ejemplos de multiplicación de fracciones decimales en una columna:



En lugar de multiplicar cualquier número por 0,1; 0,01; 0.001
puedes dividir este número por 10; 100; o 1000 respectivamente.
Por ejemplo:

22 0,1 = 2,2 ; 22: 10 = 2,2 .

Al multiplicar una fracción decimal por un número natural, debemos:

1) multiplicar los números, ignorando la coma;

2) en el producto resultante, ponga una coma para que a la derecha
de ella había tantos dígitos como en una fracción decimal.

Encontremos el producto 3.12 10 . De acuerdo con la regla anterior
primero multiplica 312 por 10 . Obtenemos: 312 10 \u003d 3120.
Y ahora separamos los dos dígitos de la derecha con una coma y obtenemos:

3,12 10 = 31,20 = 31,2 .

Entonces, al multiplicar 3.12 por 10, movimos la coma en uno
número a la derecha. Si multiplicamos 3,12 por 100, obtenemos 312, es decir
la coma se movió dos dígitos a la derecha.

3,12 100 = 312,00 = 312 .

Al multiplicar una fracción decimal por 10, 100, 1000, etc., necesitas
en esta fracción, mueva la coma a la derecha tantos caracteres como ceros haya
está en el multiplicador. Por ejemplo:

0,065 1000 = 0065, = 65 ;

2,9 1000 = 2,900 1000 = 2900, = 2900 .

Tareas sobre el tema "Multiplicación de fracciones decimales"

asistente-escolar.ru

Suma, resta, multiplicación y división de decimales

Sumar y restar decimales es similar a sumar y restar números naturales, pero con ciertas condiciones.

Regla. se compone de los dígitos de las partes enteras y fraccionarias como números naturales.

cuando se escribe suma y resta de decimales la coma que separa la parte entera de la parte fraccionaria debe estar en los términos y la suma o el minuendo, sustraendo y diferencia en una columna (una coma debajo de una coma desde la condición hasta el final del cálculo).

Suma y resta de decimales a la línea:

243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651

843,217 - 700,628 = (800 - 700) + 40 + 3 + (0,2 - 0,6) + (0,01 - 0,02) + (0,007 - 0,008) = 100 + 40 + 2 + (1,2 - 0,6) + (0,01 - 0,02) + (0,007 - 0,008) = 100 + 40 + 2 + 0,5 + (0,11 - 0,02) + (0,007 - 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 - 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 - 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589

Suma y resta de decimales en una columna:

Sumar fracciones decimales requiere una línea adicional superior para escribir números cuando la suma del dígito pasa por una decena. Restar decimales requiere que la línea extra superior marque el dígito en el que se toma prestado el 1.

Si no hay suficientes dígitos de la parte fraccionaria a la derecha del término o reducido, entonces se pueden agregar tantos ceros a la derecha en la parte fraccionaria (aumentar la profundidad de bits de la parte fraccionaria) como dígitos haya en otro término o reducido.

multiplicación de decimales se realiza de la misma forma que la multiplicación de números naturales, según las mismas reglas, pero en el producto se coloca una coma según la suma de las cifras de los factores en la parte fraccionaria, contando de derecha a izquierda (la suma de los dígitos de los factores es el número de dígitos después del punto decimal para los factores tomados en conjunto).

A multiplicando decimales en una columna, el primer dígito significativo de la derecha se firma debajo del primer dígito significativo de la derecha, como en los números naturales:

Grabación multiplicando decimales en una columna:

Grabación división decimal en una columna:

Los caracteres subrayados son caracteres que envuelven comas porque el divisor debe ser un número entero.

Regla. A división de fracciones el divisor de una fracción decimal aumenta tantos dígitos como dígitos tiene su parte fraccionaria. Para que la fracción no cambie, el dividendo aumenta en la misma cantidad de dígitos (en el dividendo y divisor, la coma se traslada a la misma cantidad de caracteres). Se coloca una coma en el cociente en la etapa de división cuando se divide la parte entera de la fracción.

Para fracciones decimales, así como para números naturales, se conserva la regla: ¡No puedes dividir un decimal por cero!

En la última lección, aprendimos a sumar y restar fracciones decimales (ver la lección "Sumar y restar fracciones decimales"). Al mismo tiempo, estimaron cuánto se simplifican los cálculos en comparación con las fracciones habituales de "dos pisos".

Desafortunadamente, con la multiplicación y división de fracciones decimales, este efecto no ocurre. En algunos casos, la notación decimal incluso complica estas operaciones.

Primero, introduzcamos una nueva definición. Lo encontraremos con bastante frecuencia, y no solo en esta lección.

La parte significativa de un número es todo lo que se encuentra entre el primer y el último dígito distinto de cero, incluidos los tráileres. Solo estamos hablando de números, no se tiene en cuenta el punto decimal.

Los dígitos incluidos en la parte significativa del número se denominan dígitos significativos. Pueden repetirse e incluso ser iguales a cero.

Por ejemplo, considere varias fracciones decimales y escriba sus partes significativas correspondientes:

1. 91,25 → 9125 (cifras significativas: 9; 1; 2; 5);
2. 0,008241 → 8241 (cifras significativas: 8; 2; 4; 1);
3. 15,0075 → 150075 (cifras significativas: 1; 5; 0; 0; 7; 5);
4. 0,0304 → 304 (cifras significativas: 3; 0; 4);
5. 3000 → 3 (solo hay una cifra significativa: 3).

Tenga en cuenta: los ceros dentro de la parte significativa del número no van a ninguna parte. Ya nos hemos encontrado con algo similar cuando aprendimos a convertir fracciones decimales en fracciones ordinarias (ver la lección “Fracciones decimales”).

Este punto es tan importante y los errores se cometen aquí con tanta frecuencia que publicaré una prueba sobre este tema en un futuro próximo. ¡Asegúrate de practicar! Y nosotros, armados con el concepto de una parte significativa, procederemos, de hecho, al tema de la lección.

multiplicación de decimales

La operación de multiplicación consta de tres pasos consecutivos:

1. Para cada fracción, escribe la parte significativa. Obtendrá dos números enteros ordinarios, sin denominadores ni puntos decimales;
2. Multiplique estos números de cualquier manera conveniente. Directamente, si los números son pequeños, o en columna. Obtenemos la parte significativa de la fracción deseada;
3. Averigüe dónde y cuántos dígitos se desplaza el punto decimal en las fracciones originales para obtener la parte significativa correspondiente. Realizar desplazamientos inversos sobre la parte significativa obtenida en el paso anterior.

Permítanme recordarles una vez más que los ceros a los lados de la parte significativa nunca se toman en cuenta. Ignorar esta regla conduce a errores.

1. 0,28 12,5;
2. 6,3 1,08;
3. 132,5 0,0034;
4. 0,0108 1600,5;
5. 5,25 10.000.

Trabajamos con la primera expresión: 0.28 12.5.

1. Escribamos las partes significativas de los números de esta expresión: 28 y 125;
2. Su producto: 28 125 = 3500;
3. En el primer multiplicador, el punto decimal se desplaza 2 dígitos a la derecha (0,28 → 28), y en el segundo, otro 1 dígito. En total, se necesita un desplazamiento a la izquierda de tres dígitos: 3500 → 3,500 = 3,5.

Ahora tratemos con la expresión 6.3 1.08.

1. Escribamos las partes significativas: 63 y 108;
2. Su producto: 63 108 = 6804;
3. De nuevo, dos desplazamientos a la derecha: de 2 y 1 dígitos, respectivamente. En total, nuevamente 3 dígitos a la derecha, por lo que el cambio inverso será de 3 dígitos a la izquierda: 6804 → 6.804. Esta vez no hay ceros al final.

Llegamos a la tercera expresión: 132.5 0.0034.

1. Partes significativas: 1325 y 34;
2. Su producto: 1325 34 = 45,050;
3. En la primera fracción, el punto decimal va 1 dígito a la derecha, y en el segundo, hasta 4. Total: 5 a la derecha. Realizamos un desplazamiento de 5 a la izquierda: 45050 → .45050 = 0.4505. El cero se eliminó al final y se agregó al frente para no dejar un punto decimal "desnudo".

La siguiente expresión: 0.0108 1600.5.

1. Escribimos partes significativas: 108 y 16 005;
2. Los multiplicamos: 108 16 005 = 1 728 540;
3. Contamos los números después del punto decimal: en el primer número hay 4, en el segundo - 1. En total - nuevamente 5. Tenemos: 1,728,540 → 17.28540 = 17.2854. Al final, se eliminó el cero "extra".

Finalmente, la última expresión: 5.25 10,000.

1. Partes significativas: 525 y 1;
2. Los multiplicamos: 525 1 = 525;
3. La primera fracción se desplaza 2 dígitos a la derecha y la segunda fracción se desplaza 4 dígitos a la izquierda (10.000 → 1,0000 = 1). Total 4 − 2 = 2 dígitos a la izquierda. Realizamos un desplazamiento inverso de 2 dígitos a la derecha: 525, → 52 500 (tuvimos que sumar ceros).

Preste atención al último ejemplo: dado que el punto decimal se mueve en diferentes direcciones, el cambio total es a través de la diferencia. ¡Este es un punto muy importante! Aquí hay otro ejemplo:

Considere los números 1.5 y 12 500. Tenemos: 1.5 → 15 (desplazamiento de 1 a la derecha); 12 500 → 125 (desplazamiento 2 a la izquierda). Damos un “paso” de 1 dígito a la derecha y luego de 2 dígitos a la izquierda. Como resultado, avanzamos 2 − 1 = 1 dígito a la izquierda.

División decimal

La división es quizás la operación más difícil. Por supuesto, aquí puede actuar por analogía con la multiplicación: dividir las partes significativas y luego "mover" el punto decimal. Pero en este caso, hay muchas sutilezas que anulan los ahorros potenciales.

Entonces, veamos un algoritmo genérico que es un poco más largo, pero mucho más confiable:

1. Convierte todos los decimales a fracciones comunes. Con un poco de práctica, este paso te llevará unos segundos;
2. Divide las fracciones resultantes de la manera clásica. En otras palabras, multiplique la primera fracción por el segundo "invertido" (vea la lección " Multiplicación y división de fracciones numéricas");
3. Si es posible, devuelva el resultado como un decimal. Este paso también es rápido, porque a menudo el denominador ya tiene una potencia de diez.

Una tarea. Encuentre el valor de la expresión:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

Consideremos la primera expresión. Primero, vamos a convertir fracciones obi a decimales:

Hacemos lo mismo con la segunda expresión. El numerador de la primera fracción se descompone nuevamente en factores:

Hay un punto importante en los ejemplos tercero y cuarto: después de deshacerse de la notación decimal, aparecen las fracciones cancelables. Sin embargo, no realizaremos esta reducción.

El último ejemplo es interesante porque el numerador de la segunda fracción es un número primo. Simplemente no hay nada que factorizar aquí, por lo que lo consideramos "en blanco":

A veces, la división da como resultado un número entero (me refiero al último ejemplo). En este caso, el tercer paso no se realiza en absoluto.

Además, al dividir suelen aparecer fracciones “feas” que no se pueden convertir a decimales. Aquí es donde la división difiere de la multiplicación, donde los resultados siempre se expresan en forma decimal. Por supuesto, en este caso, el último paso nuevamente no se realiza.

Preste atención también a los ejemplos 3 y 4. En ellos, deliberadamente no reducimos fracciones ordinarias obtenidas de decimales. De lo contrario, complicará el problema inverso: representar la respuesta final nuevamente en forma decimal.

Recuerde: la propiedad básica de una fracción (como cualquier otra regla matemática) en sí misma no significa que deba aplicarse en todas partes y siempre, en cada oportunidad.

Como números regulares.

2. Contamos el número de lugares decimales para la 1ra fracción decimal y para la 2da. Sumamos su número.

3. En el resultado final, contamos de derecha a izquierda la cantidad de dígitos que resultaron en el párrafo anterior y ponemos una coma.

Reglas para multiplicar decimales.

1. Multiplica sin prestar atención a la coma.

2. En el producto, separamos tantos dígitos después del punto decimal como hay después de las comas en ambos factores juntos.

Para multiplicar una fracción decimal por un número natural, debes:

1. Multiplica números, ignorando la coma;

2. Como resultado, ponemos una coma para que haya tantos dígitos a la derecha como en una fracción decimal.

Multiplicación de fracciones decimales por una columna.

Veamos un ejemplo:

Escribimos fracciones decimales en una columna y las multiplicamos como números naturales, ignorando las comas. Aquellos. Consideramos 3.11 como 311 y 0.01 como 1.

El resultado es 311. Luego, contamos el número de lugares decimales (dígitos) para ambas fracciones. Hay 2 dígitos en el 1er decimal y 2 en el 2. El número total de dígitos después de los puntos decimales:

2 + 2 = 4

Contamos de derecha a izquierda cuatro caracteres del resultado. En el resultado final, hay menos dígitos de los que necesita separar con una coma. En este caso, es necesario agregar el número faltante de ceros a la izquierda.

En nuestro caso, falta el primer dígito, por lo que agregamos 1 cero a la izquierda.

Nota:

Al multiplicar cualquier fracción decimal por 10, 100, 1000, etc., la coma en la fracción decimal se mueve a la derecha tantos lugares como ceros hay después del uno.

Por ejemplo:

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

Nota:

Para multiplicar un decimal por 0,1; 0,01; 0,001; y así sucesivamente, debe mover la coma a la izquierda en esta fracción tantos caracteres como ceros hay delante de la unidad.

¡Contamos cero enteros!

Por ejemplo:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

En este tutorial, veremos cada una de estas operaciones una por una.

Contenido de la lección

Sumar decimales

Como sabemos, un decimal tiene una parte entera y una parte fraccionaria. Al sumar decimales, las partes enteras y fraccionarias se suman por separado.

Por ejemplo, agreguemos los decimales 3.2 y 5.3. Es más conveniente agregar fracciones decimales en una columna.

Primero, escribimos estas dos fracciones en una columna, mientras que las partes enteras deben estar debajo de las partes enteras y las fraccionarias debajo de las partes fraccionarias. En la escuela, este requisito se llama "coma bajo coma".

Escribamos las fracciones en una columna para que la coma quede debajo de la coma:

Comenzamos a sumar las partes fraccionarias: 2 + 3 \u003d 5. Anotamos el cinco en la parte fraccionaria de nuestra respuesta:

Ahora sumamos las partes enteras: 3 + 5 = 8. Escribimos el ocho en la parte entera de nuestra respuesta:

Ahora separamos la parte entera de la parte fraccionaria con una coma. Para hacer esto, seguimos de nuevo la regla. "coma bajo coma":

Tengo la respuesta 8.5. Entonces la expresión 3.2 + 5.3 es igual a 8.5

De hecho, no todo es tan sencillo como parece a primera vista. Aquí también hay trampas, de las que hablaremos ahora.

Lugares en decimales

Los decimales, como los números ordinarios, tienen sus propios dígitos. Estos son décimos lugares, centésimos lugares, milésimos lugares. En este caso, los dígitos comienzan después del punto decimal.

El primer dígito después del punto decimal es responsable del lugar de las décimas, el segundo dígito después del punto decimal del lugar de las centésimas, el tercer dígito después del punto decimal del lugar de las milésimas.

Los dígitos decimales almacenan información útil. En particular, informan cuántos décimos, centésimos y milésimos hay en un decimal.

Por ejemplo, considere el decimal 0.345

La posición donde se encuentra el triple se llama décimo lugar

La posición donde se encuentra el cuatro se llama lugar de las centésimas

La posición donde se encuentra el cinco se llama milésimas

Miremos esta figura. Vemos que en la categoría de las décimas hay un tres. Esto sugiere que hay tres décimas en la fracción decimal 0.345.

Si sumamos las fracciones, y luego obtenemos la fracción decimal original 0.345

Se puede ver que al principio obtuvimos la respuesta, pero la convertimos a una fracción decimal y obtuvimos 0.345.

Cuando se suman fracciones decimales, se siguen los mismos principios y reglas que cuando se suman números ordinarios. La suma de fracciones decimales se produce por dígitos: se suman décimas a décimas, centésimas a centésimas, milésimas a milésimas.

Por lo tanto, al sumar fracciones decimales, se requiere seguir la regla "coma bajo coma". Una coma debajo de una coma proporciona el mismo orden en que se suman décimas a décimas, centésimas a centésimas, milésimas a milésimas.

Ejemplo 1 Encuentra el valor de la expresión 1.5 + 3.4

En primer lugar, sumamos las partes fraccionarias 5 + 4 = 9. Escribimos el nueve en la parte fraccionaria de nuestra respuesta:

Ahora sumamos las partes enteras 1 + 3 = 4. Anotamos el cuatro en la parte entera de nuestra respuesta:

Ahora separamos la parte entera de la parte fraccionaria con una coma. Para hacer esto, observamos nuevamente la regla "coma debajo de una coma":

Tengo la respuesta 4.9. Entonces el valor de la expresión 1.5 + 3.4 es 4.9

Ejemplo 2 Encuentra el valor de la expresión: 3.51 + 1.22

Escribimos esta expresión en una columna, observando la regla "coma debajo de una coma"

En primer lugar, suma la parte fraccionaria, es decir, las centésimas 1+2=3. Escribimos el triple en la centésima parte de nuestra respuesta:

Ahora suma décimas de 5+2=7. Anotamos los siete en la décima parte de nuestra respuesta:

Ahora suma las partes enteras 3+1=4. Anotamos los cuatro en toda la parte de nuestra respuesta:

Separamos la parte entera de la parte fraccionaria con una coma, observando la regla de “coma bajo la coma”:

Obtuve la respuesta 4.73. Entonces el valor de la expresión 3.51 + 1.22 es 4.73

3,51 + 1,22 = 4,73

Al igual que con los números ordinarios, al sumar fracciones decimales, . En este caso, se escribe un dígito en la respuesta y el resto se transfiere al siguiente dígito.

Ejemplo 3 Encuentra el valor de la expresión 2.65 + 3.27

Escribimos esta expresión en una columna:

Suma las centésimas de 5+7=12. El número 12 no cabrá en la centésima parte de nuestra respuesta. Por lo tanto, en la centésima, escribimos el número 2 y trasladamos la unidad al siguiente bit:

Ahora sumamos las décimas de 6+2=8 más la unidad que obtuvimos de la operación anterior, obtenemos 9. Escribimos el número 9 en la décima de nuestra respuesta:

Ahora suma las partes enteras 2+3=5. Escribimos el número 5 en la parte entera de nuestra respuesta:

Obtuve la respuesta 5.92. Entonces el valor de la expresión 2.65 + 3.27 es 5.92

2,65 + 3,27 = 5,92

Ejemplo 4 Encuentra el valor de la expresión 9.5 + 2.8

Escribe esta expresión en una columna.

Sumamos las partes fraccionarias 5 + 8 = 13. El número 13 no cabrá en la parte fraccionaria de nuestra respuesta, por lo que primero escribimos el número 3 y transferimos la unidad al siguiente dígito, o más bien la transferimos al número entero. parte:

Ahora sumamos las partes enteras 9+2=11 más la unidad que obtuvimos de la operación anterior, obtenemos 12. Escribimos el número 12 en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Tengo la respuesta 12.3. Entonces el valor de la expresión 9.5 + 2.8 es 12.3

9,5 + 2,8 = 12,3

Al sumar fracciones decimales, el número de dígitos después del punto decimal en ambas fracciones debe ser el mismo. Si no hay suficientes dígitos, estos lugares en la parte fraccionaria se llenan con ceros.

Ejemplo 5. Encuentra el valor de la expresión: 12.725 + 1.7

Antes de escribir esta expresión en una columna, hagamos que el número de dígitos después del punto decimal en ambas fracciones sea el mismo. La fracción decimal 12.725 tiene tres dígitos después del punto decimal, mientras que la fracción 1.7 tiene solo uno. Entonces, en la fracción 1.7 al final, debes agregar dos ceros. Entonces obtenemos la fracción 1,700. Ahora puedes escribir esta expresión en una columna y empezar a calcular:

Sumar milésimas de 5+0=5. Escribimos el número 5 en la milésima parte de nuestra respuesta:

Sumar centésimas de 2+0=2. Escribimos el número 2 en la centésima parte de nuestra respuesta:

Suma décimas de 7+7=14. El número 14 no cabrá en una décima parte de nuestra respuesta. Por lo tanto, primero escribimos el número 4 y transferimos la unidad al siguiente bit:

Ahora sumamos las partes enteras 12+1=13 más la unidad que obtuvimos de la operación anterior, obtenemos 14. Escribimos el número 14 en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Obtuve la respuesta 14,425. Entonces el valor de la expresión 12.725+1.700 es 14.425

12,725+ 1,700 = 14,425

Resta de decimales

Al restar fracciones decimales, debe seguir las mismas reglas que al sumar: "una coma debajo de una coma" y "un número igual de dígitos después de un punto decimal".

Ejemplo 1 Encuentra el valor de la expresión 2.5 − 2.2

Escribimos esta expresión en una columna, observando la regla de “coma bajo coma”:

Calculamos la parte fraccionaria 5−2=3. Escribimos el número 3 en la décima parte de nuestra respuesta:

Calcula la parte entera 2−2=0. Escribimos cero en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Obtuvimos la respuesta 0.3. Entonces el valor de la expresión 2.5 − 2.2 es igual a 0.3

2,5 − 2,2 = 0,3

Ejemplo 2 Encuentra el valor de la expresión 7.353 - 3.1

Esta expresión tiene un número diferente de dígitos después del punto decimal. En la fracción 7.353 hay tres dígitos después del punto decimal, y en la fracción 3.1 solo hay uno. Esto significa que en la fracción 3.1, se deben agregar dos ceros al final para que el número de dígitos en ambas fracciones sea el mismo. Entonces obtenemos 3.100.

Ahora puedes escribir esta expresión en una columna y calcularla:

Obtuve la respuesta 4,253. Entonces el valor de la expresión 7.353 − 3.1 es 4.253

7,353 — 3,1 = 4,253

Al igual que con los números ordinarios, a veces tendrá que tomar prestado uno del bit adyacente si la resta se vuelve imposible.

Ejemplo 3 Encuentra el valor de la expresión 3.46 − 2.39

Resta las centésimas de 6−9. Del número 6 no reste el número 9. Por lo tanto, debe tomar una unidad del dígito adyacente. Habiendo tomado prestado uno del dígito vecino, el número 6 se convierte en el número 16. Ahora podemos calcular las centésimas de 16−9=7. Anotamos el siete en la centésima parte de nuestra respuesta:

Ahora resta décimas. Como tomamos una unidad en la categoría de los décimos, la cifra que se ubicaba allí disminuyó en una unidad. En otras palabras, el décimo lugar ahora no es el número 4, sino el número 3. Calculemos las décimas de 3−3=0. Escribimos cero en la décima parte de nuestra respuesta:

Ahora resta las partes enteras 3−2=1. Escribimos la unidad en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Tengo la respuesta 1.07. Entonces el valor de la expresión 3.46−2.39 es igual a 1.07

3,46−2,39=1,07

Ejemplo 4. Encuentra el valor de la expresión 3−1.2

Este ejemplo resta un decimal de un entero. Escribamos esta expresión en una columna para que la parte entera de la fracción decimal 1.23 esté debajo del número 3

Ahora hagamos que el número de dígitos después del punto decimal sea el mismo. Para ello, después del número 3, pon una coma y añade un cero:

Ahora resta décimas: 0−2. No reste el número 2 de cero, por lo tanto, debe tomar una unidad del dígito adyacente. Tomando prestado uno del dígito adyacente, 0 se convierte en el número 10. Ahora puedes calcular las décimas de 10−2=8. Anotamos el ocho en la décima parte de nuestra respuesta:

Ahora resta las partes enteras. Anteriormente, el número 3 estaba ubicado en el número entero, pero le tomamos prestada una unidad. Como resultado, se convirtió en el número 2. Por lo tanto, restamos 1 de 2. 2−1=1. Escribimos la unidad en la parte entera de nuestra respuesta:

Separe la parte entera de la parte fraccionaria con una coma:

Tengo la respuesta 1.8. Entonces el valor de la expresión 3−1.2 es 1.8

multiplicación de decimales

Multiplicar decimales es fácil e incluso divertido. Para multiplicar decimales, debes multiplicarlos como números regulares, ignorando las comas.

Habiendo recibido la respuesta, es necesario separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debe contar la cantidad de dígitos después del punto decimal en ambas fracciones, luego contar la misma cantidad de dígitos a la derecha en la respuesta y colocar una coma.

Ejemplo 1 Encuentra el valor de la expresión 2.5 × 1.5

Multiplicamos estas fracciones decimales como números ordinarios, ignorando las comas. Para ignorar las comas, puede imaginar temporalmente que están completamente ausentes:

Obtuvimos 375. En este número, es necesario separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debe contar la cantidad de dígitos después del punto decimal en fracciones de 2.5 y 1.5. En la primera fracción hay un dígito después del punto decimal, en la segunda fracción también hay uno. Un total de dos números.

Volvemos al número 375 y comenzamos a movernos de derecha a izquierda. Necesitamos contar dos dígitos desde la derecha y poner una coma:

Obtuve la respuesta 3.75. Entonces el valor de la expresión 2.5 × 1.5 es 3.75

2,5 x 1,5 = 3,75

Ejemplo 2 Encuentra el valor de la expresión 12.85 × 2.7

Multipliquemos estos decimales, ignorando las comas:

Obtuvimos 34695. En este número, debe separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debe calcular la cantidad de dígitos después del punto decimal en fracciones de 12.85 y 2.7. En la fracción 12,85 hay dos dígitos después del punto decimal, en la fracción 2,7 hay un dígito, un total de tres dígitos.

Regresamos al número 34695 y comenzamos a movernos de derecha a izquierda. Necesitamos contar tres dígitos desde la derecha y poner una coma:

Obtuve la respuesta 34,695. Entonces el valor de la expresión 12.85 × 2.7 es 34.695

12,85 x 2,7 = 34,695

Multiplicar un decimal por un número regular

A veces hay situaciones en las que necesitas multiplicar una fracción decimal por un número regular.

Para multiplicar un decimal y un número ordinario, debe multiplicarlos, independientemente de la coma en el decimal. Habiendo recibido la respuesta, es necesario separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debe contar la cantidad de dígitos después del punto decimal en la fracción decimal, luego, en la respuesta, cuente la misma cantidad de dígitos a la derecha y coloque una coma.

Por ejemplo, multiplica 2,54 por 2

Multiplicamos la fracción decimal 2,54 por el número habitual 2, ignorando la coma:

Obtuvimos el número 508. En este número, debe separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, necesitas contar el número de dígitos después del punto decimal en la fracción 2.54. La fracción 2.54 tiene dos dígitos después del punto decimal.

Regresamos al número 508 y comenzamos a movernos de derecha a izquierda. Necesitamos contar dos dígitos desde la derecha y poner una coma:

Tengo la respuesta 5.08. Entonces el valor de la expresión 2.54 × 2 es 5.08

2,54x2 = 5,08

Multiplicar decimales por 10, 100, 1000

La multiplicación de decimales por 10, 100 o 1000 se hace de la misma manera que la multiplicación de decimales por números regulares. Es necesario realizar la multiplicación, ignorando la coma en la fracción decimal, luego en la respuesta, separar la parte entera de la parte fraccionaria, contando la misma cantidad de dígitos a la derecha que dígitos después del punto decimal en el decimal fracción.

Por ejemplo, multiplica 2,88 por 10

Multipliquemos la fracción decimal 2.88 por 10, ignorando la coma en la fracción decimal:

Obtuvimos 2880. En este número, debe separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, necesitas contar el número de dígitos después del punto decimal en la fracción 2.88. Vemos que en la fracción 2.88 hay dos dígitos después del punto decimal.

Regresamos al número 2880 y comenzamos a movernos de derecha a izquierda. Necesitamos contar dos dígitos desde la derecha y poner una coma:

Obtuve la respuesta 28.80. Descartamos el último cero: obtenemos 28,8. Entonces el valor de la expresión 2.88 × 10 es 28.8

2,88 x 10 = 28,8

Hay una segunda manera de multiplicar fracciones decimales por 10, 100, 1000. Este método es mucho más simple y conveniente. Consiste en que la coma en la fracción decimal se desplaza a la derecha tantos dígitos como ceros hay en el multiplicador.

Por ejemplo, resolvamos el ejemplo anterior 2.88×10 de esta manera. Sin dar ningún cálculo, inmediatamente miramos el factor 10. Nos interesa cuántos ceros hay en él. Vemos que tiene un cero. Ahora en la fracción 2.88 movemos el punto decimal un dígito a la derecha, obtenemos 28.8.

2,88 x 10 = 28,8

Intentemos multiplicar 2.88 por 100. Inmediatamente miramos el factor 100. Nos interesa cuántos ceros hay en él. Vemos que tiene dos ceros. Ahora en la fracción 2.88 movemos el punto decimal dos dígitos a la derecha, obtenemos 288

2,88 x 100 = 288

Intentemos multiplicar 2.88 por 1000. Inmediatamente miramos el factor 1000. Nos interesa cuántos ceros hay en él. Vemos que tiene tres ceros. Ahora en la fracción 2.88 movemos el punto decimal tres dígitos a la derecha. El tercer dígito no está, así que agregamos otro cero. Como resultado, obtenemos 2880.

2,88 x 1000 = 2880

Multiplicar decimales por 0,1 0,01 y 0,001

Multiplicar decimales por 0,1, 0,01 y 0,001 funciona de la misma manera que multiplicar un decimal por un decimal. Es necesario multiplicar fracciones como números ordinarios, y poner una coma en la respuesta, contando tantos dígitos a la derecha como dígitos hay después del punto decimal en ambas fracciones.

Por ejemplo, multiplica 3,25 por 0,1

Multiplicamos estas fracciones como números ordinarios, ignorando las comas:

Obtuvimos 325. En este número, debes separar la parte entera de la parte fraccionaria con una coma. Para hacer esto, debe calcular la cantidad de dígitos después del punto decimal en fracciones de 3.25 y 0.1. En la fracción 3,25 hay dos dígitos después del punto decimal, en la fracción 0,1 hay un dígito. Un total de tres números.

Volvemos al número 325 y comenzamos a movernos de derecha a izquierda. Necesitamos contar tres dígitos a la derecha y poner una coma. Después de contar tres dígitos, encontramos que los números han terminado. En este caso, debe agregar un cero y poner una coma:

Obtuvimos la respuesta 0.325. Entonces el valor de la expresión 3.25 × 0.1 es 0.325

3,25 x 0,1 = 0,325

Hay una segunda forma de multiplicar decimales por 0,1, 0,01 y 0,001. Este método es mucho más fácil y conveniente. Consiste en que la coma en la fracción decimal se desplaza hacia la izquierda tantos dígitos como ceros hay en el multiplicador.

Por ejemplo, resolvamos el ejemplo anterior 3,25 × 0,1 de esta manera. Sin dar ningún cálculo, inmediatamente miramos el factor 0.1. Estamos interesados ​​en cuántos ceros hay en él. Vemos que tiene un cero. Ahora en la fracción 3.25 movemos el punto decimal un dígito a la izquierda. Moviendo la coma un dígito a la izquierda, vemos que no hay más dígitos antes del tres. En este caso, suma un cero y pon una coma. Como resultado, obtenemos 0.325

3,25 x 0,1 = 0,325

Intentemos multiplicar 3,25 por 0,01. Mire inmediatamente el multiplicador de 0.01. Estamos interesados ​​en cuántos ceros hay en él. Vemos que tiene dos ceros. Ahora en la fracción 3.25 movemos la coma a la izquierda dos dígitos, obtenemos 0.0325

3,25 x 0,01 = 0,0325

Intentemos multiplicar 3,25 por 0,001. Mire inmediatamente el multiplicador de 0.001. Estamos interesados ​​en cuántos ceros hay en él. Vemos que tiene tres ceros. Ahora en la fracción 3.25 movemos el punto decimal a la izquierda tres dígitos, obtenemos 0.00325

3,25 × 0,001 = 0,00325

No confundas multiplicar decimales por 0,1, 0,001 y 0,001 con multiplicar por 10, 100, 1000. Un error común que comete la mayoría de la gente.

Al multiplicar por 10, 100, 1000, la coma se mueve hacia la derecha tantos dígitos como ceros hay en el multiplicador.

Y al multiplicar por 0,1, 0,01 y 0,001, la coma se desplaza hacia la izquierda tantos dígitos como ceros haya en el multiplicador.

Si al principio le cuesta recordar, puede utilizar el primer método, en el que la multiplicación se realiza como con los números ordinarios. En la respuesta, deberá separar la parte entera de la parte fraccionaria contando tantos dígitos a la derecha como dígitos haya después del punto decimal en ambas fracciones.

Dividir un número más pequeño por uno más grande. Nivel avanzado.

En una de las lecciones anteriores dijimos que al dividir un número menor por otro mayor se obtiene una fracción, en cuyo numerador está el dividendo, y en el denominador está el divisor.

Por ejemplo, para dividir una manzana en dos, debe escribir 1 (una manzana) en el numerador y escribir 2 (dos amigos) en el denominador. El resultado es una fracción. Entonces cada amigo obtendrá una manzana. En otras palabras, media manzana. Una fracción es la respuesta a un problema. como dividir una manzana entre dos

Resulta que puedes resolver este problema aún más si divides 1 por 2. Después de todo, una barra fraccionaria en cualquier fracción significa división, lo que significa que esta división también está permitida en una fracción. ¿Pero cómo? Estamos acostumbrados a que el dividendo sea siempre mayor que el divisor. Y aquí, por el contrario, el dividendo es menor que el divisor.

Todo se aclarará si recordamos que una fracción significa triturar, dividir, dividir. Esto significa que la unidad se puede dividir en tantas partes como desee, y no solo en dos partes.

Al dividir un número menor por uno mayor se obtiene una fracción decimal, en la que la parte entera será 0 (cero). La parte fraccionaria puede ser cualquier cosa.

Entonces, dividamos 1 entre 2. Resolvamos este ejemplo con una esquina:

Uno no se puede dividir en dos así como así. si haces una pregunta "cuantos dos hay en uno" , entonces la respuesta será 0. Por lo tanto, en privado escribimos 0 y ponemos una coma:

Ahora, como de costumbre, multiplicamos el cociente por el divisor para sacar el resto:

Ha llegado el momento en que la unidad se puede dividir en dos partes. Para hacer esto, agregue otro cero a la derecha del recibido:

Obtuvimos 10. Dividimos 10 entre 2, obtenemos 5. Anotamos el cinco en la parte fraccionaria de nuestra respuesta:

Ahora sacamos el último resto para completar el cálculo. Multiplicamos 5 por 2, obtenemos 10

Obtuvimos la respuesta 0.5. Entonces la fracción es 0.5

Media manzana también se puede escribir usando la fracción decimal 0.5. Si sumamos estas dos mitades (0,5 y 0,5), obtenemos de nuevo la manzana entera original:

Este punto también se puede entender si imaginamos cómo se divide 1 cm en dos partes. Si divides 1 centímetro en 2 partes, obtienes 0,5 cm.

Ejemplo 2 Encuentra el valor de la expresión 4:5

¿Cuántos cinco hay en cuatro? De nada. Escribimos en privado 0 y ponemos una coma:

Multiplicamos 0 por 5, obtenemos 0. Escribimos cero debajo del cuatro. Inmediatamente reste este cero del dividendo:

Ahora comencemos a dividir (dividir) los cuatro en 5 partes. Para ello, a la derecha de 4, sumamos cero y dividimos 40 por 5, nos sale 8. Escribimos el ocho en privado.

Completamos el ejemplo multiplicando 8 por 5, y obtenemos 40:

Obtuvimos la respuesta 0.8. Entonces el valor de la expresión 4:5 es 0.8

Ejemplo 3 Encuentra el valor de la expresión 5: 125

¿Cuántos números 125 hay en cinco? De nada. Escribimos 0 en privado y ponemos una coma:

Multiplicamos 0 por 5, obtenemos 0. Escribimos 0 debajo del cinco. Inmediatamente restar de los cinco 0

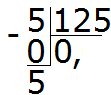
Ahora comencemos a dividir (dividir) los cinco en 125 partes. Para ello, a la derecha de este cinco, escribimos el cero:

Divide 50 por 125. ¿Cuántos números 125 hay en 50? De nada. Entonces en el cociente escribimos nuevamente 0

Multiplicamos 0 por 125, obtenemos 0. Escribimos este cero debajo de 50. Inmediatamente restamos 0 de 50

Ahora dividimos el número 50 en 125 partes. Para ello, a la derecha de 50, escribimos otro cero:

Divide 500 entre 125. Cuantos numeros hay 125 en el numero 500. En el numero 500 hay cuatro numeros 125. Escribimos los cuatro en privado:

Completamos el ejemplo multiplicando 4 por 125, y obtenemos 500

Obtuvimos la respuesta 0.04. Entonces el valor de la expresión 5: 125 es 0.04

División de números sin resto

Entonces, pongamos una coma en el cociente después de la unidad, indicando así que la división de partes enteras ha terminado y pasamos a la parte fraccionaria:

Sumar cero al resto 4

Ahora dividimos 40 por 5, nos sale 8. Escribimos el ocho en privado:

40−40=0. Recibió 0 en el resto. Entonces la división está completamente completa. Dividir 9 por 5 da como resultado un decimal de 1,8:

9: 5 = 1,8

Ejemplo 2. Dividir 84 entre 5 sin resto

Primero dividimos 84 por 5 como de costumbre con un resto:

Recibido en privado 16 y 4 mas en el saldo. Ahora dividimos este resto por 5. Ponemos una coma en el privado, y le sumamos 0 al resto 4

Ahora dividimos 40 entre 5, obtenemos 8. Escribimos el ocho en el cociente después del punto decimal:

y completa el ejemplo comprobando si todavía queda un resto:

Dividir un decimal por un número regular

Una fracción decimal, como sabemos, consta de un número entero y una parte fraccionaria. Al dividir una fracción decimal por un número regular, primero que nada necesitas:

• dividir la parte entera de la fracción decimal por este número;
• después de dividir la parte entera, debe colocar inmediatamente una coma en la parte privada y continuar con el cálculo, como en la división ordinaria.

Por ejemplo, dividamos 4,8 entre 2

Escribamos este ejemplo como una esquina:

Ahora dividamos la parte entera por 2. Cuatro dividido por dos es dos. Escribimos el deuce en privado e inmediatamente ponemos una coma:

Ahora multiplicamos el cociente por el divisor y vemos si queda resto de la división:

4−4=0. El resto es cero. No escribimos cero todavía, ya que la solución no está completa. Luego continuamos calculando, como en la división ordinaria. Saca 8 y divídelo por 2

8: 2 = 4. Escribimos el cuatro en el cociente e inmediatamente lo multiplicamos por el divisor:

Tengo la respuesta 2.4. Valor de expresión 4.8: 2 es igual a 2.4

Ejemplo 2 Encuentra el valor de la expresión 8.43:3

Dividimos 8 por 3, obtenemos 2. Inmediatamente pon una coma después de los dos:

Ahora multiplicamos el cociente por el divisor 2 × 3 = 6. Escribimos el seis debajo del ocho y hallamos el resto:

Dividimos 24 entre 3, nos sale 8. Escribimos el ocho en privado. Inmediatamente lo multiplicamos por el divisor para encontrar el resto de la división:

24−24=0. El resto es cero. El cero aún no está registrado. Tome los últimos tres del dividendo y divida por 3, obtenemos 1. Inmediatamente multiplique 1 por 3 para completar este ejemplo:

Tengo la respuesta 2.81. Entonces el valor de la expresión 8.43: 3 es igual a 2.81

Dividir un decimal entre un decimal

Para dividir una fracción decimal en una fracción decimal, en el dividendo y en el divisor, mueva la coma hacia la derecha la misma cantidad de dígitos que hay después del punto decimal en el divisor, y luego divida por un número regular.

Por ejemplo, divide 5,95 entre 1,7

Escribamos esta expresión como una esquina

Ahora, en el dividendo y en el divisor, desplazamos la coma a la derecha la misma cantidad de dígitos que hay después del punto decimal en el divisor. El divisor tiene un dígito después del punto decimal. Entonces debemos mover la coma a la derecha un dígito en el dividendo y en el divisor. Transferencia:

Después de mover el punto decimal un dígito a la derecha, la fracción decimal 5,95 se convirtió en una fracción 59,5. Y la fracción decimal 1,7, después de mover el punto decimal un dígito a la derecha, se convirtió en el número habitual 17. Y ya sabemos cómo dividir la fracción decimal entre el número habitual. El cálculo adicional no es difícil:

La coma se mueve a la derecha para facilitar la división. Esto está permitido debido a que al multiplicar o dividir el dividendo y el divisor por el mismo número, el cociente no cambia. ¿Qué significa?

Esta es una de las características interesantes de la división. Se llama propiedad privada. Considere la expresión 9: 3 = 3. Si en esta expresión el dividendo y el divisor se multiplican o dividen por el mismo número, entonces el cociente 3 no cambiará.

Multipliquemos el dividendo y el divisor por 2 y veamos qué sucede:

(9 × 2) : (3 × 2) = 18: 6 = 3

Como se puede ver en el ejemplo, el cociente no ha cambiado.

Lo mismo sucede cuando llevamos una coma en el dividendo y en el divisor. En el ejemplo anterior, donde dividimos 5,91 entre 1,7, movimos la coma un dígito a la derecha en el dividendo y el divisor. Después de mover la coma, la fracción 5,91 se convirtió en la fracción 59,1 y la fracción 1,7 se convirtió en el número habitual 17.

De hecho, dentro de este proceso, tuvo lugar la multiplicación por 10. Así es como se veía:

5,91 × 10 = 59,1

Por lo tanto, el número de dígitos después del punto decimal en el divisor depende de por qué se multiplicarán el dividendo y el divisor. En otras palabras, el número de dígitos después del punto decimal en el divisor determinará cuántos dígitos en el dividendo y en el divisor se moverá la coma a la derecha.

División decimal por 10, 100, 1000

Dividir un decimal por 10, 100 o 1000 se hace de la misma manera que . Por ejemplo, dividamos 2,1 entre 10. Resolvamos este ejemplo con una esquina:

Pero también hay una segunda forma. es más ligero La esencia de este método es que la coma en el dividendo se mueve hacia la izquierda tantos dígitos como ceros hay en el divisor.

Resolvamos el ejemplo anterior de esta manera. 2.1: 10. Miramos el divisor. Estamos interesados ​​en cuántos ceros hay en él. Vemos que hay un cero. Entonces, en el divisible 2.1, debe mover la coma a la izquierda un dígito. Movemos la coma a la izquierda un dígito y vemos que no quedan más dígitos. En este caso, añadimos un cero más antes del número. Como resultado, obtenemos 0.21

Intentemos dividir 2,1 entre 100. Hay dos ceros en el número 100. Entonces, en el divisible 2.1, debe mover la coma a la izquierda dos dígitos:

2,1: 100 = 0,021

Intentemos dividir 2,1 entre 1000. Hay tres ceros en el número 1000. Entonces, en el divisible 2.1, debe mover la coma a la izquierda tres dígitos:

2,1: 1000 = 0,0021

División decimal por 0,1, 0,01 y 0,001

Dividir un decimal por 0.1, 0.01 y 0.001 se hace de la misma manera que . En el dividendo y en el divisor, debe mover la coma hacia la derecha tantos dígitos como haya después del punto decimal en el divisor.

Por ejemplo, dividamos 6,3 entre 0,1. En primer lugar, movemos las comas en el dividendo y en el divisor hacia la derecha el mismo número de dígitos que hay después del punto decimal en el divisor. El divisor tiene un dígito después del punto decimal. Así que movemos las comas en el dividendo y en el divisor un dígito a la derecha.

Después de mover el punto decimal un dígito a la derecha, la fracción decimal 6,3 se convierte en el número habitual 63, y la fracción decimal 0,1, después de mover el punto decimal un dígito a la derecha, se convierte en uno. Y dividir 63 entre 1 es muy sencillo:

Entonces el valor de la expresión 6.3: 0.1 es igual a 63

Pero también hay una segunda forma. es más ligero La esencia de este método es que la coma en el dividendo se transfiere a la derecha tantos dígitos como ceros hay en el divisor.

Resolvamos el ejemplo anterior de esta manera. 6.3:0.1. Miremos el divisor. Estamos interesados ​​en cuántos ceros hay en él. Vemos que hay un cero. Entonces, en el divisible 6.3, debe mover la coma a la derecha un dígito. Movemos la coma a la derecha un dígito y obtenemos 63

Intentemos dividir 6,3 entre 0,01. El divisor 0.01 tiene dos ceros. Entonces, en el divisible 6.3, debe mover la coma a la derecha dos dígitos. Pero en el dividendo solo hay un dígito después del punto decimal. En este caso, se debe agregar un cero más al final. Como resultado, obtenemos 630

Intentemos dividir 6,3 entre 0,001. El divisor de 0.001 tiene tres ceros. Entonces, en el divisible 6.3, debe mover la coma a la derecha tres dígitos:

6,3: 0,001 = 6300

Tareas para solución independiente

¿Te gustó la lección?
Únase a nuestro nuevo grupo Vkontakte y comience a recibir notificaciones de nuevas lecciones