Predavanje 3 Opći teoremi dinamike

Dinamika sustava materijalnih točaka je važna grana teorijske mehanike. Ovdje se uglavnom razmatraju problemi gibanja mehaničkih sustava (sustava materijalnih točaka) s konačnim brojem stupnjeva slobode - maksimalnim brojem neovisnih parametara koji određuju položaj sustava. Glavni zadatak dinamike sustava je proučavanje zakona gibanja krutog tijela i mehaničkih sustava.

Najjednostavniji pristup proučavanju gibanja sustava koji se sastoji od N materijalnih točaka, svodi se na razmatranje gibanja svake pojedine točke sustava. U tom slučaju moraju se odrediti sve sile koje djeluju na svaku točku sustava, uključujući i sile međudjelovanja između točaka.

Određivanjem akceleracije svake točke u skladu s drugim Newtonovim zakonom (1.2) dobivamo za svaku točku tri skalarna diferencijalna zakona gibanja drugog reda, tj. 3 N diferencijalni zakon gibanja cijelog sustava.

Za pronalaženje jednadžbi gibanja mehaničkog sustava za zadane sile i početne uvjete za svaku točku sustava potrebno je integrirati dobivene diferencijalne zakone. Taj je zadatak težak čak i u slučaju dviju materijalnih točaka koje se gibaju samo pod djelovanjem međudjelovanja sila prema zakonu univerzalnog privlačenja (problem dvaju tijela), a izuzetno težak u slučaju triju međusobno djelujućih točaka (problem triju tijela). ).

Stoga je potrebno pronaći takve metode rješavanja problema koje bi dovele do rješivih jednadžbi i dale predodžbu o gibanju mehaničkog sustava. Opći teoremi dinamike, kao posljedica diferencijalnih zakona gibanja, omogućuju izbjegavanje složenosti koja nastaje tijekom integracije i dobivanje potrebnih rezultata.

3.1. Opće napomene

Točke mehaničkog sustava bit će numerirane indeksima ja, j, k itd. koji se provlače kroz sve vrijednosti 1, 2, 3… N, gdje N je broj bodova sustava. Fizičke veličine vezane uz k th točke označene su istim indeksom kao točka. Na primjer, oni izražavaju radijus vektor i brzinu k-ta točka.

Na svaku od točaka sustava djeluju sile dvaju izvora: prvo, sile čiji su izvori izvan sustava, tzv. vanjski sile i označena sa ; drugo, sile iz drugih točaka ovog sustava, tzv unutarnje sile i označava se sa . Unutarnje sile zadovoljavaju treći Newtonov zakon. Razmotrite najjednostavnija svojstva unutarnjih sila koje djeluju na cijeli mehanički sustav u bilo kojem od njegovih stanja.

Prvo imanje. Geometrijski zbroj svih unutarnjih sila sustava (glavni vektor unutarnjih sila) jednak je nuli.

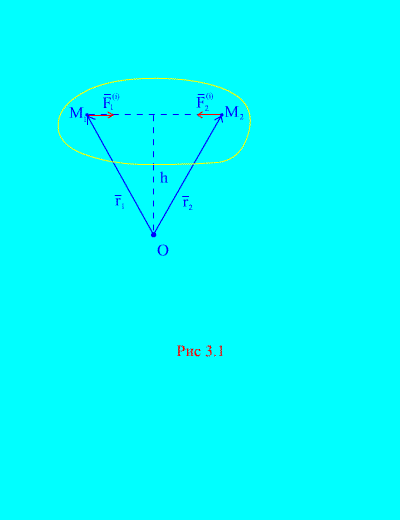
Doista, ako razmotrimo bilo koje dvije proizvoljne točke sustava, na primjer, i (Sl. 3.1), zatim za njih , jer sile akcije i reakcije uvijek su jednake po apsolutnoj vrijednosti, one djeluju duž jedne linije djelovanja u suprotnom smjeru, koja povezuje točke međusobnog djelovanja. Glavni vektor unutarnjih sila sastoji se od parova sila međusobno djelujućih točaka, dakle

(3.1)

Drugo svojstvo. Geometrijski zbroj momenata svih unutarnjih sila u odnosu na proizvoljnu točku u prostoru jednak je nuli.

Razmotrimo sustav momenata sila i s obzirom na točku O(Sl. 3.1). Iz (Sl. 3.1). jasno je da

,

jer obje sile imaju iste krake i suprotne smjerove vektorskih momenata. Glavni moment unutarnjih sila oko točke O sastoji se od vektorske sume takvih izraza i jednaka je nuli. Posljedično,

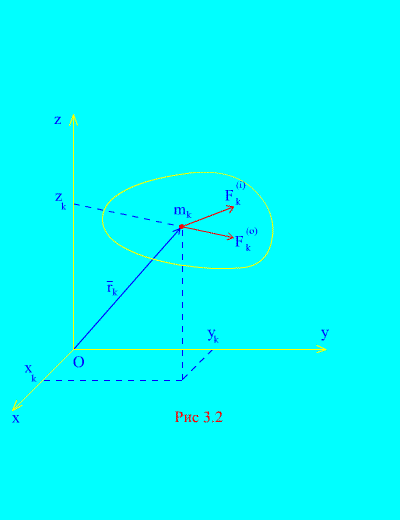
Neka vanjske i unutarnje sile djeluju na mehanički sustav koji se sastoji od N bodova (Sl. 3.2). Ako se rezultanta vanjskih sila i rezultanta svih unutarnjih sila primijeni na svaku točku sustava, tada za bilo koju k točke sustava, mogu se sastaviti diferencijalne jednadžbe gibanja. Ukupno će takve jednadžbe biti N:

a u projekcijama na nepomične koordinatne osi 3 N:

(3.4)

Vektorske jednadžbe (3.3) ili ekvivalentne skalarne jednadžbe (3.4) predstavljaju diferencijalne zakone gibanja materijalnih točaka cijelog sustava. Ako se sve točke kreću paralelno s jednom ravninom ili jednom ravnom crtom, tada će broj jednadžbi (3.4) u prvom slučaju biti 2 N, u drugom N.

Primjer 1 Dva tereta mase i međusobno su povezana neistegljivim kabelom prebačenim preko bloka (Sl. 3.3). Zanemarujući sile trenja, kao i masu bloka i sajle, određuju zakon kretanja tereta i napetost sajle.

Riješenje. Sustav se sastoji od dva materijalna tijela (povezana nerastegljivim kabelom) koja se kreću paralelno s jednom osi X. Zapišimo diferencijalne zakone gibanja u projekcijama na os x za sve.

Desni uteg neka se spušta s ubrzanjem, zatim će se lijevi uteg ubrzano podizati. Mentalno se oslobađamo veze (kabla) i nadomještamo je reakcijama i (Sl. 3.3). Uz pretpostavku da su tijela slobodna, sastavit ćemo diferencijalne zakone gibanja u projekciji na os x(što znači da su napetosti niti unutarnje sile, a težina tereta vanjske):

Budući da je i (tijela su povezana neistegljivim kabelom), dobivamo

Rješavanje ovih jednadžbi za ubrzanje i napetost užeta T, dobivamo

.

Imajte na umu da napetost kabela na nije jednaka gravitaciji odgovarajućeg opterećenja.

3. 2. Teorem o gibanju središta mase

Poznato je da se kruto tijelo i mehanički sustav u ravnini mogu prilično teško kretati. Do prvog teorema o gibanju tijela i mehaničkog sustava može se doći na sljedeći način: ispustiti c.-l. predmet koji se sastoji od mnogo čvrstih tijela međusobno pričvršćenih. Jasno je da će letjeti u paraboli. To je otkriveno pri proučavanju gibanja točke. Međutim, sada objekt nije točka. Okreće se, njiše u procesu letenja oko nekog efektivnog središta, koje se kreće duž parabole. Prvi teorem o gibanju složenih objekata kaže da je određeno efektivno središte središte mase tijela koje se kreće. Centar mase nije nužno smješten u samom tijelu, može ležati i negdje izvan njega.

Teorema. Središte mase mehaničkog sustava kreće se kao materijalna točka s masom jednakom masi cijelog sustava, na koju djeluju sve vanjske sile koje djeluju na sustav.

Da bismo dokazali teorem, prepisujemo diferencijalne zakone gibanja (3.3) u sljedećem obliku:

(3.5)

gdje N je broj bodova sustava.

Zbrojimo jednadžbe član po član:

(a)

Položaj središta mase mehaničkog sustava u odnosu na odabrani koordinatni sustav određen je formulom (2.1): gdje M je masa sustava. Zatim se zapisuje lijeva strana jednakosti (a).

Prvi zbroj, koji stoji na desnoj strani jednakosti (a), jednak je glavnom vektoru vanjskih sila, a posljednji, po svojstvu unutarnjih sila, jednak je nuli. Tada će se jednakost (a), uzimajući u obzir (b), prepisati

, (3.6)

oni. umnožak mase sustava i akceleracije središta njegove mase jednak je geometrijskom zbroju svih vanjskih sila koje djeluju na sustav.

Iz jednadžbe (3.6) proizlazi da unutarnje sile ne utječu izravno na gibanje središta mase. Međutim, u nekim slučajevima oni su uzrok pojave vanjskih sila koje djeluju na sustav. Dakle, unutarnje sile koje rotiraju pogonske kotače automobila uzrokuju djelovanje vanjske sile prianjanja koja se primjenjuje na obruč kotača.

Primjer 2 Mehanizam, smješten u okomitoj ravnini, postavljen je na vodoravnu glatku ravninu i pričvršćen na nju šipkama čvrsto pričvršćenim na površinu. Do i L (Sl. 3.4).

Radijus diska 1 R nepomična. Disk 2 masa m i radijus r pričvršćuje se kurbilom, duž R+ r u točki od 2. Ručica se vrti konstantno

kutna brzina. U početnom trenutku ručica je zauzela desni vodoravni položaj. Zanemarujući masu koljena, odredite najveće horizontalne i vertikalne sile koje djeluju na poluge, ako je ukupna masa okvira i kotača 1 jednaka M. Također razmotrite ponašanje mehanizma u nedostatku šipki.

Riješenje. Sustav se sastoji od dvije mase ( N=2 ): nepomični disk 1 s okvirom i pomični disk 2. Usmjerimo os. na kroz težište nepomičnog diska okomito prema gore, os x- duž horizontalne ravnine.

Teorem o gibanju centra mase (3.6) zapisujemo u koordinatnom obliku

Vanjske sile ovog sustava su: težina okvira i fiksnog diska - mg, težina pokretnog diska mg, - ukupna horizontalna reakcija vijaka, - normalna ukupna reakcija ravnine. Posljedično,

Zatim se prepisuju zakoni gibanja (b).

Izračunajmo koordinate centra mase mehaničkog sustava:

; (G)

kako se vidi iz (Sl. 3.4), , , (kut zakretanja ručice), . Zamjena ovih izraza u (r) i izračunavanje druge derivacije u odnosu na vrijeme t od , , dobivamo to

(e)

Zamjenom (c) i (e) u (b), nalazimo

Horizontalni pritisak koji djeluje na šipke je najveći i najmanji kada cos = 1 odnosno, tj.

Pritisak mehanizma na horizontalnu ravninu ima najveću i najmanju vrijednost kada grijeh odnosno, tj.

Zapravo, prvi problem dinamike je riješen: prema poznatim jednadžbama gibanja centra mase sustava (e), obnavljaju se sile koje sudjeluju u gibanju.

U nedostatku rešetki K i L (Sl. 3.4), mehanizam može početi poskakivati ​​iznad vodoravne ravnine. To će se dogoditi kada, tj. kada , slijedi da kutna brzina rotacije koljena, pri kojoj mehanizam odskače, mora zadovoljiti jednakost

.

3. 3. Zakon očuvanja gibanja centra mase

Ako je glavni vektor vanjskih sila koje djeluju na sustav jednak nuli, tj. , zatim od(3.6)slijedi da je akceleracija centra mase nula, dakle, brzina centra mase je konstantna po veličini i smjeru. Ako, naime, u početnom trenutku centar mase miruje, onda ono miruje sve vrijeme dok glavni vektor vanjskih sila ne bude jednak nuli.

Nekoliko korolara slijedi iz ovog teorema.

· Same unutarnje sile ne mogu promijeniti prirodu gibanja središta mase sustava.

· Ako je glavni vektor vanjskih sila koje djeluju na sustav jednak nuli, tada središte mase miruje ili se giba jednoliko i pravocrtno.

· Ako je projekcija glavnog vektora vanjskih sila sustava na neku nepomičnu os jednaka nuli, tada se projekcija brzine centra mase sustava na tu os ne mijenja.

· Nekoliko sila koje djeluju na kruto tijelo ne mogu promijeniti kretanje njegova središta mase (mogu izazvati samo rotaciju tijela oko središta mase).

Razmotrimo primjer koji ilustrira zakon očuvanja gibanja središta mase.

Primjer 3 Dva utega s masama i povezani su nerastezljivom niti prebačenom preko bloka (Sl. 3.5), fiksiran na klinu s masom M. Klin leži na glatkoj horizontalnoj ravnini. U početku je sustav bio u stanju mirovanja. Nađite pomak klina duž ravnine kada se prvi teret spusti na visinu N. Zanemarite masu bloka i niti.

Riješenje. Vanjske sile koje zajedno s utezima djeluju na klin su sile gravitacije, i mg, kao i normalni odziv glatke horizontalne površine N. Prema tome,

Kako je sustav u početnom trenutku mirovao, imamo .

Izračunajmo koordinatu središta mase sustava u i u trenutku t 1 kada je težina tereta g spustiti se na visinu H.

Na trenutak:

,

gdje , , X- odnosno koordinate središta mase tereta težine g, g i težine klina Mg.

Pretpostavimo da se klin u trenutku giba u pozitivnom smjeru osi Vol po iznosu L ako težina tereta padne na visinu N. Zatim, na trenutak

jer opterećenja zajedno s klinom će se pomaknuti na L udesno, a uteg će se pomaknuti za udaljenost uz klin. Budući da , nakon izračuna dobivamo

.

3.4. Sustav količine kretanja

3.4.1. Izračunavanje impulsa sustava

Količina gibanja materijalne točke vektorska je veličina jednaka umnošku mase točke i vektora njezine brzine

Jedinica mjerenja količine kretanja -

Količina gibanja mehaničkog sustava naziva se vektorska suma količine gibanja pojedinih točaka sustava, tj.

gdje N je broj bodova sustava.

Količina gibanja mehaničkog sustava može se izraziti preko mase sustava M i brzina centra mase. Stvarno,

oni. količina gibanja sustava jednaka je umnošku mase cijelog sustava i brzine njegova središta mase. Smjer je isti kao i smjer (Sl. 3.6)

U projekcijama na pravokutne osi imamo

gdje su , , - projekcije brzine centra mase sustava.

Ovdje M je masa mehaničkog sustava; ne mijenja kako se sustav kreće.

Posebno je zgodno koristiti ove rezultate pri proračunu momenta krutih tijela.

Iz formule (3.7) je vidljivo da ako se mehanički sustav giba tako da njegovo središte mase ostaje nepomično, tada količina gibanja sustava ostaje jednaka nuli.

3.4.2. Elementarni i puni impuls snage

Djelovanje sile na materijalnu točku tijekom vremena dt može se okarakterizirati elementarnim impulsom. Ukupni impuls sile u vremenu t, ili impuls sile , određuje se formulom

ili u projekcijama na koordinate osi

(3.8a)

Jedinica impulsa sile je .

3.4.3. Teorem o promjeni količine gibanja sustava

Neka vanjske i unutarnje sile djeluju na točke sustava. Tada za svaku točku sustava možemo primijeniti diferencijalne zakone gibanja (3.3), imajući u vidu da :

.

Zbrajanjem po svim točkama sustava dobivamo

Po svojstvu unutarnjih sila i po definiciji imamo

(3.9)

Množenje obje strane ove jednadžbe sa dt, dobivamo teorem o promjeni količine gibanja u diferencijalnom obliku:

, (3.10)

oni. diferencijal količine gibanja mehaničkog sustava jednak je vektorskom zbroju elementarnih impulsa svih vanjskih sila koje djeluju na točke mehaničkog sustava.

Izračunavanje integrala oba dijela (3.10) kroz vrijeme od 0 do t, dobivamo teorem u konačnom ili integralnom obliku

(3.11)

U projekcijama na koordinatne osi imat ćemo

Promjena količine gibanja mehaničkog sustava tijekom vremenat, jednak je vektorskom zbroju svih impulsa vanjskih sila koje djeluju na točke mehaničkog sustava u istom vremenu.

Primjer 4 Opterećenje mase m spušta niz kosu ravninu iz mirovanja pod djelovanjem sile F, proporcionalno vremenu: , gdje (Sl. 3.7). Kolika je brzina tijela nakon t sekundi nakon početka gibanja, ako je koeficijent trenja klizanja tereta na kosoj ravnini jednak f.

Riješenje. Oslikajmo sile koje djeluju na teret: mg - težina tereta, N je normalna reakcija ravnine, je sila trenja klizanja tereta na ravnini i . Smjer svih sila prikazan je u (Sl. 3.7).

Usmjerimo os x niz nagnutu ravninu. Napišimo teorem o promjeni količine gibanja (3.11) u projekciji na os x:

(a)

Po uvjetu, jer u početnom trenutku teret je mirovao. Zbroj projekcija impulsa svih sila na x-osu je

Posljedično,

,

.

3.4.4. Zakoni očuvanja količine gibanja

Zakoni očuvanja dobiveni su kao posebni slučajevi teorema o promjeni količine gibanja. Moguća su dva posebna slučaja.

· Ako je vektorski zbroj svih vanjskih sila koje djeluju na sustav jednak nuli, tj. , onda to slijedi iz teorema (3.9) , što ,

oni. ako je glavni vektor vanjskih sila sustava jednak nuli, tada je količina gibanja sustava konstantna po veličini i smjeru.

· Ako je projekcija glavnog vektora vanjskih sila na bilo koju koordinatnu os jednaka nuli, npr. Ox, tj. , tada je projekcija količine gibanja na ovu os konstantna.

Razmotrimo primjer primjene zakona o održanju količine gibanja.

Primjer 5 Balističko njihalo je tijelo mase ovješeno na dugačkoj niti (Sl. 3.8).

Metak mase koji se kreće brzinom V i padajući u nepomično tijelo, zaglavi se u njemu, a tijelo se otkloni. Kolika je bila brzina metka ako se tijelo podigne u visinu h ?

Riješenje. Neka tijelo sa zaglavljenim metkom dobije brzinu. Zatim, koristeći zakon održanja količine gibanja u međudjelovanju dva tijela, možemo napisati .

Brzina se može izračunati pomoću zakona održanja mehaničke energije . Zatim . Kao rezultat toga nalazimo

.

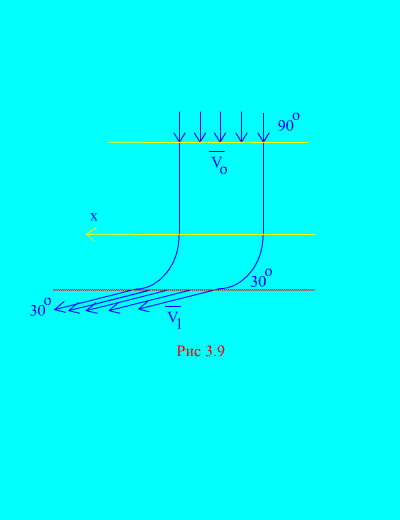
Primjer 6. Voda ulazi u fiksni kanal (Sl. 3.9) promjenjivi odsjek s brzinom pod kutom prema horizontu; površina poprečnog presjeka kanala na ulazu; brzina vode na izlazu iz kanala i zaklapa s horizontom kut.

Odredite horizontalnu komponentu reakcije koju voda vrši na stijenke kanala. Gustoća vode .

Riješenje. Odredit ćemo horizontalnu komponentu reakcije stijenki kanala na vodu. Ta je sila jednaka po apsolutnoj vrijednosti i suprotnog predznaka željenoj sili. Imamo, prema (3.11a),

. (a)

Izračunavamo masu volumena tekućine koja ulazi u kanal tijekom vremena t:

Vrijednost rAV 0 zove se druga masa - masa tekućine koja teče kroz bilo koji dio cijevi po jedinici vremena.

Ista količina vode napusti kanal za isto vrijeme. U uvjetu su zadane početna i konačna brzina.

Izračunajmo desnu stranu jednakosti (a) koja određuje zbroj projekcija na horizontalnu os vanjskih sila koje djeluju na sustav (vodu). Jedina horizontalna sila je horizontalna komponenta rezultantne reakcije zidova Rx. Ta je sila konstantna tijekom ravnomjernog gibanja vode. Zato

. (u)

Zamjenom (b) i (c) u (a), dobivamo

3.5. Kinetički moment sustava

3.5.1. Glavni moment količine gibanja sustava

Neka je radijus vektor točke s masom sustava u odnosu na neku točku A, koja se naziva središte (Sl. 3.10).

Moment količine gibanja (kinetički moment) točke u odnosu na centar A nazvan vektor , određena formulom

. (3.12)

U ovom slučaju, vektor usmjerena okomito na ravninu koja prolazi središtem ALI i vektor .

Moment količine gibanja (kinetički moment) točke oko osi naziva se projekcija kutne količine gibanja točke u odnosu na bilo koje središte odabrano na ovoj osi na ovu os.

Glavni moment količine gibanja (kinetički moment) sustava u odnosu na središte A naziva se količina

(3.13)

Glavni moment količine gibanja (kinetički moment) sustava oko osi naziva se projekcija na ovu os glavnog momenta količine gibanja sustava u odnosu na bilo koji odabrani na danom središnja os.

3.5.2. Moment rotacijskog krutog tijela oko osi rotacije

Kompatibilna fiksna točka O tijelo koje leži na osi rotacije Oz, s ishodištem koordinatnog sustava Ohuz, čije će se osi okretati s tijelom (Sl. 3.11). Neka je radijus-vektor točke tijela u odnosu na ishodište koordinata, njegove projekcije na osi označit ćemo s , , . Projekcije vektora kutne brzine tijela na iste osi označit ćemo s 0, 0, ().

Promotrimo gibanje određenog sustava materijalnih volumena u odnosu na fiksni koordinatni sustav. Kada sustav nije slobodan, tada se može smatrati slobodnim, ako odbacimo ograničenja nametnuta sustavu i zamijenimo njihovo djelovanje odgovarajućim reakcijama.

Podijelimo sve sile koje djeluju na sustav na vanjske i unutarnje; oba mogu uključivati ​​reakcije odbačenog

veze. Označimo s i glavni vektor i glavni moment vanjskih sila u odnosu na točku A.

1. Teorem o promjeni količine gibanja. Ako je impuls sustava, tada (vidi )

tj. Vrijedi teorem: vremenska derivacija količine gibanja sustava jednaka je glavnom vektoru svih vanjskih sila.

Zamjenom vektora njegovim izrazom gdje je masa sustava, brzina centra mase, jednadžba (4.1) se može dati u drugom obliku:

Ova jednakost znači da se središte mase sustava giba kao materijalna točka čija je masa jednaka masi sustava i na koju djeluje sila koja je geometrijski jednaka glavnom vektoru svih vanjskih sila sustava. Posljednja tvrdnja naziva se teorem o gibanju središta mase (centra tromosti) sustava.

Ako tada iz (4.1) slijedi da je vektor količine gibanja konstantan po veličini i smjeru. Projicirajući ga na koordinatnu os, dobivamo tri skalarna prva integrala diferencijalnih jednadžbi dvostrukog lanca sustava:

Ti se integrali nazivaju integrali impulsa. Kada je brzina centra mase konstantna, tj. giba se jednoliko i pravocrtno.

Ako je projekcija glavnog vektora vanjskih sila na bilo koju os, npr. na os, jednaka nuli, tada imamo jedan prvi integral, ili ako su dvije projekcije glavnog vektora jednake nuli, tada postoje dva integrala količine gibanja.

2. Teorem o promjeni kinetičkog momenta. Neka je A neka proizvoljna točka u prostoru (pokretna ili nepokretna), koja se ne mora nužno poklapati s nekom određenom materijalnom točkom sustava tijekom cijelog vremena gibanja. Njegovu brzinu u fiksnom koordinatnom sustavu označavamo kao Teorem o promjeni kutne količine gibanja materijalnog sustava u odnosu na točku A ima oblik

Ako je točka A fiksna, tada jednakost (4.3) ima jednostavniji oblik:

Ova jednakost izražava teorem o promjeni kutne količine gibanja sustava u odnosu na fiksnu točku: vremenska derivacija kutne količine gibanja sustava, izračunata u odnosu na neku fiksnu točku, jednaka je glavnom momentu svih vanjskih sila relativnih do ove točke.

Ako je tada prema (4.4) vektor kutne količine gibanja konstantan po veličini i smjeru. Projicirajući ga na koordinatnu os, dobivamo skalarne prve integrale diferencijalnih jednadžbi gibanja sustava:

Ti se integrali nazivaju integrali kutne količine gibanja ili integrali površina.

Ako se točka A podudara sa središtem mase sustava, tada prvi član na desnoj strani jednakosti (4.3) nestaje i teorem o promjeni kutne količine gibanja ima isti oblik (4.4) kao u slučaju fiksnu točku A. Imajte na umu (vidi 4 § 3) da se u razmatranom slučaju apsolutna kutna količina gibanja sustava na lijevoj strani jednakosti (4.4) može zamijeniti jednakom kutnom količinom gibanja sustava u njegovom gibanju relativno prema centar mase.

Neka je neka konstantna os ili os konstantnog smjera koja prolazi kroz središte mase sustava, i neka je kutni moment sustava u odnosu na tu os. Iz (4.4) slijedi da

gdje je moment vanjskih sila u odnosu na os. Ako tijekom cijelog vremena gibanja tada imamo prvi integral

U radovima S. A. Chaplygina dobiveno je nekoliko generalizacija teorema o promjeni kutne količine gibanja, koje su zatim primijenjene u rješavanju niza problema o kotrljanju kuglica. Daljnje generalizacije teorema o promjeni kpnetološkog momenta i njihove primjene u problemima dinamike krutog tijela sadržane su u radovima. Glavni rezultati ovih radova vezani su uz teorem o promjeni kutne količine gibanja u odnosu na pokretnu, koja stalno prolazi kroz neku pokretnu točku A. Neka je jedinični vektor usmjeren duž ove osi. Množenjem skalarno s obje strane jednakosti (4.3) i dodavanjem člana na oba njezina dijela, dobivamo

Kada je ispunjen kinematski uvjet

jednadžba (4.5) slijedi iz (4.7). A ako je uvjet (4.8) zadovoljen tijekom cijelog vremena gibanja, tada prvi integral (4.6) postoji.

Ako su veze sustava idealne i dopuštaju rotaciju sustava kao krutog tijela oko osi iu broju virtualnih pomaka, tada je glavni moment reakcija oko osi i jednak nuli, a tada je vrijednost na desna strana jednadžbe (4.5) je glavni moment svih vanjskih djelatnih sila oko osi i . Jednakost nuli ovog momenta i zadovoljivost relacije (4.8) bit će u razmatranom slučaju dovoljni uvjeti za postojanje integrala (4.6).

Ako je smjer osi i nepromijenjen, tada se uvjet (4.8) može napisati kao

Ova jednakost znači da su projekcije brzine centra mase i brzine točke A na os i na ravninu okomitu na nju paralelne. U radu S. A. Chaplygina, umjesto (4.9), zahtijeva se manje opći uvjet gdje je X proizvoljna konstanta.

Uočimo da uvjet (4.8) ne ovisi o izboru točke na . Doista, neka je P proizvoljna točka na osi. Zatim

i zbog toga

Zaključno, bilježimo geometrijsku interpretaciju Resalovih jednadžbi (4.1) i (4.4): vektori apsolutnih brzina krajeva vektora i jednaki su glavnom vektoru i glavnom momentu svih vanjskih sila u odnosu na točka A.

Ministarstvo obrazovanja i znanosti Ruske Federacije

Savezna državna proračunska obrazovna ustanova visokog stručnog obrazovanja

"Kubanjsko državno tehnološko sveučilište"

Teorijska mehanika

Dio 2 dinamike

Odobreno od Uredništva i nakladništva

sveučilišno vijeće kao

vodič za učenje

Krasnodar

UDK 531.1/3 (075)

Teorijska mehanika. Dio 2. Dinamika: Udžbenik / L.I.Draiko; Kuban. država tehnol.un-t. Krasnodar, 2011. 123 str.

ISBN 5-230-06865-5

Teorijski materijal je predstavljen u sažetom obliku, dani su primjeri rješavanja problema, od kojih većina odražava stvarne tehničke probleme, pozornost je posvećena izboru racionalne metode rješenja.

Dizajniran za prvostupnike dopisnog učenja i učenja na daljinu u područjima građevinarstva, prometa i strojarstva.

tab. 1 sl. 68 Bibliografija. 20 naslova

Znanstveni urednik kandidat tehničkih znanosti, izv. prof. V.F. Melnikov

Recenzenti: Predstojnik Zavoda za teorijsku mehaniku i teoriju mehanizama i strojeva Kubanskog agrarnog sveučilišta prof. F.M. Kanarev; Izvanredni profesor Odsjeka za teorijsku mehaniku Kubanskog državnog tehnološkog sveučilišta M.E. Multih

Objavljeno odlukom Uredničkog i izdavačkog vijeća Kubanskog državnog tehnološkog sveučilišta.

Ponovno izdavanje

ISBN 5-230-06865-5 KubGTU 1998

Predgovor

Ovaj udžbenik namijenjen je izvanrednim studentima građevinarstva, prometa i inženjerskih specijalnosti, ali se može koristiti pri proučavanju odjeljka "Dinamika" kolegija teorijske mehanike od strane izvanrednih studenata drugih specijalnosti, kao i redovitih studenata s samostalan rad.

Priručnik je sastavljen u skladu s važećim programom kolegija teorijske mehanike, pokriva sva pitanja glavnog dijela kolegija. Svaki dio sadrži kratku teoretsku građu, opremljenu ilustracijama i smjernicama za korištenje u rješavanju problema. Priručnik analizira rješenje 30 zadataka, odražavajući stvarne tehnološke probleme i odgovarajuće kontrolne zadatke za samostalno rješavanje. Za svaki zadatak prikazana je računska shema koja jasno ilustrira rješenje. Dizajn rješenja usklađen je sa zahtjevima za dizajn ispita izvanrednih studenata.

Autor izražava duboku zahvalnost nastavnicima Katedre za teorijsku mehaniku i teoriju mehanizama i strojeva Kubanskog agrarnog sveučilišta za njihov veliki rad u recenziji udžbenika, kao i nastavnicima Katedre za teorijsku mehaniku Kubanske države Tehnološkom sveučilištu na vrijednim komentarima i savjetima u pripremi udžbenika za tisak.

Sve kritičke primjedbe i želje autor će ubuduće primati sa zahvalnošću.

Uvod

Dinamika je najvažnija grana teorijske mehanike. Većina specifičnih zadataka koji se javljaju u inženjerskoj praksi odnosi se na dinamiku. Koristeći se zaključcima statike i kinematike, dinamika utvrđuje opće zakonitosti gibanja materijalnih tijela pod djelovanjem primijenjenih sila.

Najjednostavniji materijalni objekt je materijalna točka. Za materijalnu točku može se uzeti materijalno tijelo bilo kojeg oblika čije se dimenzije u razmatranom problemu mogu zanemariti. Tijelo konačnih dimenzija može se uzeti kao materijalna točka ako razlika u gibanju njegovih točaka nije značajna za dani problem. To se događa kada su dimenzije tijela male u usporedbi s udaljenostima koje prolaze točke tijela. Svaka se čestica krutog tijela može smatrati materijalnom točkom.

Sile koje djeluju na točku ili materijalno tijelo dinamički se ocjenjuju po njihovom dinamičkom utjecaju, tj. po tome kako mijenjaju karakteristike gibanja materijalnih objekata.

Kretanje materijalnih objekata kroz vrijeme odvija se u prostoru u odnosu na određeni referentni okvir. U klasičnoj mehanici, na temelju Newtonovih aksioma, prostor se smatra trodimenzionalnim, njegova svojstva ne ovise o materijalnim objektima koji se u njemu kreću. Položaj točke u takvom prostoru određen je s tri koordinate. Vrijeme nije povezano s prostorom i kretanjem materijalnih objekata. Smatra se istim za sve referentne sustave.

Zakoni dinamike opisuju kretanje materijalnih objekata u odnosu na apsolutne koordinatne osi, koje se konvencionalno smatraju nepokretnima. Ishodište apsolutnog koordinatnog sustava uzima se u središtu Sunca, a osi su usmjerene na udaljene, uvjetno nepomične zvijezde. Pri rješavanju mnogih tehničkih problema, koordinatne osi povezane sa Zemljom mogu se smatrati uvjetno nepokretnima.

Parametri mehaničkog gibanja materijalnih objekata u dinamici utvrđeni su matematičkim izvodima iz osnovnih zakona klasične mehanike.

Prvi zakon (zakon inercije):

Materijalna točka održava stanje mirovanja ili jednolikog i pravocrtnog gibanja sve dok je djelovanje bilo koje sile ne izvede iz tog stanja.

Jednoliko i pravocrtno gibanje točke naziva se gibanje po inerciji. Mirovanje je poseban slučaj gibanja po inerciji, kada je brzina točke nula.

Svaka materijalna točka ima inerciju, tj. nastoji održati stanje mirovanja ili ravnomjernog pravocrtnog gibanja. Referentni okvir, u odnosu na koji je zadovoljen zakon tromosti, naziva se inercijalni, a gibanje promatrano u odnosu na taj okvir naziva se apsolutnim. Svaki referentni okvir koji izvodi translatorno pravocrtno i jednoliko gibanje u odnosu na inercijski okvir također će biti inercijski okvir.

Drugi zakon (osnovni zakon dinamike):

Ubrzanje materijalne točke u odnosu na inercijski referentni okvir proporcionalno je sili koja djeluje na točku i podudara se sa silom u smjeru:
.

Iz osnovnog zakona dinamike proizlazi da sa silom
ubrzanje
. Masa točke karakterizira stupanj otpora točke na promjenu njezine brzine, odnosno mjera je tromosti materijalne točke.

Treći zakon (zakon akcije i reakcije):

Sile kojima dva tijela djeluju jedno na drugo jednake su veličine i usmjerene duž jedne ravne crte u suprotnim smjerovima.

Sile koje se nazivaju akcija i reakcija djeluju na različita tijela i stoga ne tvore uravnoteženi sustav.

Četvrti zakon (zakon neovisnosti djelovanja sila):

Uz istovremeno djelovanje više sila, ubrzanje materijalne točke jednako je geometrijskom zbroju ubrzanja koje bi točka imala pod djelovanjem svake sile zasebno:

, gdje
,
,…,
.

Često je moguće izolirati važne značajke gibanja mehaničkog sustava bez pribjegavanja integriranju sustava diferencijalnih jednadžbi gibanja. To se postiže primjenom općih teorema dinamike.

5.1. Osnovni pojmovi i definicije

Vanjske i unutarnje sile. Svaka sila koja djeluje na točku mehaničkog sustava nužno je ili aktivna sila ili reakcija sprezanja. Cijeli skup sila koje djeluju na točke sustava možemo različito podijeliti u dvije klase: na vanjske sile i unutarnje sile (indeksi e i i - od latinskih riječi externus - vanjski i internus - unutarnji). Vanjske sile nazivaju se sile koje na točke sustava djeluju iz točaka i tijela koja nisu dio promatranog sustava. Sile međudjelovanja između točaka i tijela razmatranog sustava nazivaju se unutarnjim.

Ova podjela ovisi o tome koje materijalne točke i tijela istraživač uključuje u razmatrani mehanički sustav. Ako se sastav sustava proširi tako da uključuje dodatne točke i tijela, tada neke sile koje su bile vanjske za prethodni sustav mogu postati unutarnje za prošireni sustav.

Svojstva unutarnjih sila. Budući da su te sile sile međudjelovanja između dijelova sustava, one su uključene u cjeloviti sustav unutarnjih sila u "dvoje" organizirane prema aksiomu akcija-reakcija. Svaka takva "dvojka" sila

glavni vektor i glavni moment oko proizvoljnog središta jednaki su nuli. Budući da se kompletan sustav unutarnjih sila sastoji samo od »dvojki«, dakle

1) glavni vektor sustava unutarnjih sila jednak je nuli,

2) glavni moment sustava unutarnjih sila u odnosu na proizvoljnu točku jednak je nuli.

Masa sustava je aritmetički zbroj masa mk svih točaka i tijela koja čine sustav:

centar gravitacije(središte tromosti) mehaničkog sustava je geometrijska točka C čiji su radijus vektor i koordinate određeni formulama

gdje su radijus vektori i koordinate točaka koje čine sustav.

Za kruto tijelo u jednoličnom gravitacijskom polju položaji središta mase i težišta se podudaraju, u ostalim slučajevima to su različite geometrijske točke.

Zajedno s inercijskim referentnim okvirom, često se istovremeno razmatra i neinercijalni referentni okvir koji se kreće naprijed. Njegove koordinatne osi (Koenigove osi) biraju se tako da se referentna točka C uvijek poklapa sa središtem mase mehaničkog sustava. U skladu s definicijom, centar mase je fiksiran u Koenigovim osima i nalazi se u ishodištu koordinata.

Moment tromosti sustava u odnosu na os naziva se skalarna veličina jednaka zbroju umnožaka masa mk svih točaka sustava s kvadratima njihovih udaljenosti od osi:

Ako je mehanički sustav kruto tijelo, da biste pronašli 12, možete koristiti formulu

gdje je gustoća, volumen koji tijelo zauzima.