วิธีคูณจำนวนเต็มด้วยทศนิยม การคูณทศนิยม: กฎ ตัวอย่าง วิธีแก้

§ 107 การเพิ่มเติม ทศนิยม.

การบวกทศนิยมก็เหมือนกับการบวกจำนวนเต็ม เรามาดูสิ่งนี้พร้อมตัวอย่าง

1) 0.132 + 2.354 ลองติดป้ายกำกับคำหนึ่งไว้ด้านล่างอีกคำหนึ่ง

ตรงนี้ เมื่อบวก 2 ในพันถึง 4 ในพันจะทำให้เกิด 6 ในพัน;
จากบวก 3 ในร้อยกับ 5 ในร้อย ผลลัพธ์คือ 8 ในร้อย
จากการเพิ่ม 1 ใน 10 ด้วย 3 ใน 10 -4 ใน 10 และ
จากการบวกจำนวนเต็ม 0 ด้วยจำนวนเต็ม 2 - 2 จำนวนเต็ม

2) 5,065 + 7,83.

ไม่มีหลักพันในเทอมที่สอง ดังนั้นจึงเป็นเรื่องสำคัญที่จะไม่ทำผิดพลาดเมื่อติดป้ายกำกับคำศัพท์ทีละคำ

3) 1,2357 + 0,469 + 2,08 + 3,90701.

ตรงนี้ เมื่อบวกหนึ่งในพัน ผลลัพธ์ที่ได้คือ 21 ในพัน เราเขียน 1 ไว้ใต้หลักพัน และเพิ่ม 2 เข้ากับหลักร้อย ดังนั้นในตำแหน่งที่ร้อยเราจึงได้เทอมต่อไปนี้: 2 + 3 + 6 + 8 + 0; รวมพวกเขาให้ 19 ในร้อย เราเซ็นสัญญา 9 อันเดอร์ร้อย 1 นับเป็นสิบ ฯลฯ

ดังนั้นเมื่อเพิ่มเศษส่วนทศนิยมจะต้องปฏิบัติตามลำดับต่อไปนี้: ลงชื่อเศษส่วนหนึ่งที่อยู่ด้านล่างอีกอันเพื่อให้ในทุกเงื่อนไขตัวเลขเดียวกันอยู่ใต้กันและเครื่องหมายจุลภาคทั้งหมดอยู่ในคอลัมน์แนวตั้งเดียวกัน ทางด้านขวาของจุดทศนิยมของบางเทอมจะมีการกำหนดให้เลขศูนย์ดังกล่าวอย่างน้อยก็ทางจิตใจ เพื่อให้ทุกพจน์ที่อยู่หลังจุดทศนิยมมี หมายเลขเดียวกันตัวเลข จากนั้นพวกเขาทำการบวกด้วยตัวเลขโดยเริ่มจากด้านขวาและในผลรวมที่ได้จะใส่ลูกน้ำในคอลัมน์แนวตั้งเดียวกันกับที่อยู่ในข้อกำหนดเหล่านี้

§ 108. การลบเศษส่วนทศนิยม

การลบทศนิยมมีวิธีการเดียวกับการลบจำนวนเต็ม มาแสดงสิ่งนี้ด้วยตัวอย่าง

1) 9.87 - 7.32. ลองเซ็นชื่อย่อยใต้ minuend เพื่อให้หน่วยของตัวเลขเดียวกันอยู่ใต้กัน:

2) 16.29 - 4.75. เรามาลงนามใน subtrahend ใต้ minuend ดังตัวอย่างแรก:

หากต้องการลบสิบ คุณต้องนำหนึ่งหน่วยทั้งหมดจาก 6 แล้วแบ่งออกเป็นสิบ.

3) 14.0213- 5.350712. มาเซ็นชื่อย่อยใต้ minuend:

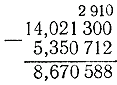
การลบทำได้ดังนี้: เนื่องจากเราไม่สามารถลบ 2 ในล้านจาก 0 ได้ เราจึงควรหมุนไปยังหลักที่ใกล้ที่สุดทางซ้าย เช่น ไปที่หลักแสน แต่แทนที่หลักแสนก็มีศูนย์เช่นกัน ดังนั้นเราจึงนำ 1 หนึ่งหมื่นจากสามหมื่นและเราแบ่งออกเป็นแสนส่วน เราได้ 10 แสนส่วน ซึ่งเราเหลือ 9 แสนส่วนไว้ในหมวดแสนส่วน และเราแบ่ง 1 แสนส่วนเป็นล้าน เราได้ 10 ส่วนในล้าน ดังนั้นใน สามอันสุดท้ายเราได้ตัวเลขต่อไปนี้: 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 เพื่อความชัดเจนและความสะดวกยิ่งขึ้น (เพื่อไม่ให้ลืม) ตัวเลขเหล่านี้จะถูกเขียนไว้เหนือเลขเศษส่วนที่สอดคล้องกันของเครื่องหมาย minuend ตอนนี้คุณสามารถเริ่มลบได้ จาก 10 ในล้าน เราลบ 2 ในล้าน เราจะได้ 8 ในล้าน จาก 9 แสนส่วน เราลบ 1 แสนส่วน เราได้ 8 แสนส่วน เป็นต้น

ดังนั้นเมื่อลบเศษส่วนทศนิยมให้สังเกตลำดับต่อไปนี้: ลงชื่อลบใต้เครื่องหมายลบเพื่อให้ตัวเลขเดียวกันอยู่ใต้กันและเครื่องหมายจุลภาคทั้งหมดอยู่ในคอลัมน์แนวตั้งเดียวกัน ทางด้านขวาพวกเขาบวกอย่างน้อยในใจจำนวนศูนย์จำนวนมากใน minuend หรือ subtrahend เพื่อให้มีจำนวนหลักเท่ากันจากนั้นจึงลบออกด้วยตัวเลขโดยเริ่มจากด้านขวาและในผลต่างที่ได้จึงใส่ลูกน้ำไว้ คอลัมน์แนวตั้งเดียวกับที่อยู่ใน minuend และลบออก

§ 109. การคูณเศษส่วนทศนิยม

มาดูตัวอย่างการคูณเศษส่วนทศนิยมกัน

ในการค้นหาผลคูณของตัวเลขเหล่านี้ เราสามารถหาเหตุผลได้ดังนี้ หากตัวประกอบเพิ่มขึ้น 10 เท่า ตัวประกอบทั้งสองจะเป็นจำนวนเต็ม จากนั้นเราก็สามารถคูณพวกมันได้ตามกฎการคูณจำนวนเต็ม แต่เรารู้ว่าเมื่อปัจจัยหนึ่งเพิ่มขึ้นหลายครั้ง ผลิตภัณฑ์ก็จะเพิ่มขึ้นด้วยปริมาณที่เท่ากัน ซึ่งหมายความว่า จำนวนที่ได้จากการคูณตัวประกอบจำนวนเต็ม เช่น 28 ด้วย 23 นั้นมากกว่าผลคูณจริง 10 เท่า และเพื่อให้ได้ งานที่แท้จริงคุณต้องลดสินค้าที่พบลง 10 เท่า ดังนั้นตรงนี้คุณจะต้องคูณด้วย 10 หนึ่งครั้งและหารด้วย 10 หนึ่งครั้ง แต่การคูณและหารด้วย 10 ทำได้โดยการเลื่อนจุดทศนิยมไปทางขวาและซ้ายไปจุดเดียว ดังนั้นคุณต้องทำสิ่งนี้: ในปัจจัยให้ย้ายลูกน้ำไปทางขวาหนึ่งตำแหน่งซึ่งจะทำให้ได้เท่ากับ 23 จากนั้นคุณต้องคูณจำนวนเต็มผลลัพธ์:

สินค้าชิ้นนี้ใหญ่กว่าของจริงถึง 10 เท่า ดังนั้นจึงจะต้องลดลง 10 เท่า โดยให้เลื่อนลูกน้ำไปทางซ้ายหนึ่งตำแหน่ง ดังนั้นเราจึงได้

28 2,3 = 64,4.

เพื่อวัตถุประสงค์ในการตรวจสอบคุณสามารถเขียนเศษส่วนทศนิยมด้วยตัวส่วนและดำเนินการตามกฎสำหรับการคูณเศษส่วนสามัญเช่น

2) 12,27 0,021.

ข้อแตกต่างระหว่างตัวอย่างนี้กับตัวอย่างก่อนหน้าก็คือ ทั้งสองปัจจัยจะแสดงเป็นเศษส่วนทศนิยม แต่ที่นี่ ในกระบวนการคูณ เราจะไม่ใส่ใจกับลูกน้ำ เช่น เราจะเพิ่มตัวคูณ 100 เท่าชั่วคราว และตัวคูณ 1,000 เท่า ซึ่งจะเพิ่มผลคูณ 100,000 เท่า ดังนั้น เมื่อคูณ 1,227 ด้วย 21 เราจะได้:

1 227 21 = 25 767.

เมื่อพิจารณาว่าผลลัพธ์ที่ได้มีขนาดใหญ่กว่าผลิตภัณฑ์จริง 100,000 เท่า ตอนนี้เราต้องลดขนาดลง 100,000 เท่าโดยใส่ลูกน้ำให้ถูกต้อง จากนั้นเราจะได้:

32,27 0,021 = 0,25767.

มาตรวจสอบกัน:

ดังนั้น ในการคูณเศษส่วนทศนิยมสองตัว ก็เพียงพอแล้วโดยไม่ต้องสนใจเครื่องหมายจุลภาค คูณเศษส่วนเป็นจำนวนเต็มและในผลคูณให้แยกตำแหน่งทศนิยมให้มากที่สุดเท่าที่จะเป็นไปได้ด้วยเครื่องหมายจุลภาคทางด้านขวาเท่ากับที่มีอยู่ในตัวคูณและ ในตัวคูณด้วยกัน

ตัวอย่างสุดท้ายส่งผลให้ผลิตภัณฑ์มีทศนิยมห้าตำแหน่ง หากไม่ต้องการความแม่นยำมากเช่นนั้น เศษส่วนทศนิยมจะถูกปัดเศษ เมื่อปัดเศษ คุณควรใช้กฎเดียวกันกับที่ระบุไว้สำหรับจำนวนเต็ม

§ 110 การคูณโดยใช้ตาราง

การคูณทศนิยมบางครั้งสามารถทำได้โดยใช้ตาราง เพื่อจุดประสงค์นี้ คุณสามารถใช้ตารางสูตรคูณสำหรับตัวเลขสองหลักได้ ตามที่อธิบายไว้ก่อนหน้านี้

1) คูณ 53 ด้วย 1.5

เราจะคูณ 53 ด้วย 15 ในตาราง ผลคูณนี้เท่ากับ 795 เราพบผลคูณ 53 ด้วย 15 แต่ปัจจัยที่สองของเราน้อยกว่า 10 เท่า ซึ่งหมายความว่าผลิตภัณฑ์จะต้องลดลง 10 เท่า กล่าวคือ

53 1,5 = 79,5.

2) คูณ 5.3 ด้วย 4.7

อันดับแรก เราพบผลคูณของ 53 คูณ 47 ในตาราง ซึ่งจะเป็น 2,491 แต่เนื่องจากเราเพิ่มตัวคูณและตัวคูณทั้งหมด 100 เท่า ผลลัพธ์ที่ได้จึงมากกว่าที่ควรจะเป็น 100 เท่า ดังนั้นเราจึงต้องลดผลิตภัณฑ์นี้ลง 100 เท่า:

5,3 4,7 = 24,91.

3) คูณ 0.53 ด้วย 7.4

ขั้นแรก เราพบในตารางผลิตภัณฑ์ 53 x 74 มันจะเป็น 3,922 แต่เนื่องจากเราเพิ่มตัวคูณขึ้น 100 เท่า และตัวคูณ 10 เท่า ผลคูณก็เพิ่มขึ้น 1,000 เท่า ตอนนี้เราต้องลดมันลง 1,000 เท่า:

0,53 7,4 = 3,922.

§ 111. การหารเศษส่วนทศนิยม

เราจะดูการหารเศษส่วนทศนิยมตามลำดับนี้:

1. การหารเศษส่วนทศนิยมด้วย จำนวนเต็ม,

1. หารเศษส่วนทศนิยมด้วยจำนวนเต็ม

1) หาร 2.46 ด้วย 2

เราหารด้วย 2 จำนวนเต็มแรก จากนั้นจึงสิบและสุดท้ายในร้อย

2) หาร 32.46 ด้วย 3

32,46: 3 = 10,82.

เราหาร 3 สิบด้วย 3 จากนั้นเริ่มหาร 2 หน่วยด้วย 3 เนื่องจากจำนวนหน่วยเงินปันผลคือ (2) น้อยกว่าตัวหาร(3) จากนั้นฉันต้องใส่ 0 เข้าไปในผลหาร; ยิ่งกว่านั้น ส่วนที่เหลือเราเอา 4 ในสิบมาหาร 24 ในสิบด้วย 3; ได้ 8 ใน 10 ของผลหาร และสุดท้ายก็หาร 6 ในร้อย

3) หาร 1.2345 ด้วย 5

1,2345: 5 = 0,2469.

ในส่วนผลหาร ตำแหน่งแรกคือจำนวนเต็มศูนย์ เนื่องจากจำนวนเต็มหนึ่งหารด้วย 5 ไม่ลงตัว

4) หาร 13.58 ด้วย 4

ความพิเศษของตัวอย่างนี้คือ เมื่อเราได้รับ 9 ในร้อยจากผลหาร เราพบว่าเศษเหลือเท่ากับ 2 ในร้อย เราแบ่งเศษนี้ออกเป็นพัน ๆ ได้ 20 ในพัน และหารเสร็จ.

กฎ.การหารเศษส่วนทศนิยมด้วยจำนวนเต็มจะดำเนินการในลักษณะเดียวกับการหารจำนวนเต็ม และผลลัพธ์ที่เหลือจะถูกแปลงเป็นเศษส่วนทศนิยม ซึ่งเล็กลงและเล็กลง การหารดำเนินต่อไปจนกว่าส่วนที่เหลือจะเป็นศูนย์

2. หารทศนิยมด้วยทศนิยม

1) หาร 2.46 ด้วย 0.2

เรารู้วิธีหารเศษส่วนทศนิยมด้วยจำนวนเต็มแล้ว ลองคิดดูว่าเป็นไปได้ไหมที่จะลดกรณีการแบ่งใหม่นี้ลงเหลือเพียงกรณีก่อนหน้า? ครั้งหนึ่ง เราพิจารณาคุณสมบัติอันน่าทึ่งของผลหาร ซึ่งประกอบด้วยข้อเท็จจริงที่ว่ามันยังคงไม่เปลี่ยนแปลงเมื่อเงินปันผลและตัวหารเพิ่มขึ้นหรือลดลงพร้อมกันในจำนวนเท่าเดิม เราสามารถหารตัวเลขที่ให้มาได้ง่ายๆ ถ้าตัวหารเป็นจำนวนเต็ม. ในการทำเช่นนี้ก็เพียงพอที่จะเพิ่มขึ้น 10 เท่าและเพื่อให้ได้ผลหารที่ถูกต้องจำเป็นต้องเพิ่มเงินปันผลในจำนวนที่เท่ากันนั่นคือ 10 เท่า จากนั้นการหารตัวเลขเหล่านี้จะถูกแทนที่ด้วยการหารตัวเลขต่อไปนี้:

อีกทั้งไม่จำเป็นต้องแก้ไขรายละเอียดใดๆ อีกต่อไป

เรามาทำแผนกนี้กัน:

ดังนั้น 2.46: 0.2 = 12.3

2) หาร 1.25 ด้วย 1.6

เราเพิ่มตัวหาร (1.6) ขึ้น 10 เท่า เพื่อให้ผลหารไม่เปลี่ยนแปลง เราจะเพิ่มเงินปันผล 10 เท่า จำนวนเต็ม 12 จำนวนหารด้วย 16 ไม่ลงตัว ดังนั้นเราจึงเขียน 0 ลงในผลหารและหาร 125 ในสิบด้วย 16 เราจะได้ 7 ในสิบของผลหารและเศษ 13 เราแบ่ง 13 ในสิบออกเป็นร้อยโดยกำหนดให้ 0 และหาร 130 ในร้อยด้วย 16 ฯลฯ โปรดทราบสิ่งต่อไปนี้:

ก) เมื่อไม่มีจำนวนเต็มในตัวใดจำนวนหนึ่ง จะมีการเขียนจำนวนเต็มเป็นศูนย์แทน

b) เมื่อหลังจากบวกตัวเลขของเงินปันผลเข้ากับส่วนที่เหลือแล้ว จะได้ตัวเลขที่หารด้วยตัวหารไม่ลงตัว จากนั้นศูนย์จะถูกเขียนในรูปผลหาร

c) เมื่อหลังจากลบหลักสุดท้ายของการจ่ายเงินปันผลแล้ว การหารไม่สิ้นสุด จากนั้นเมื่อบวกศูนย์เข้ากับส่วนที่เหลือ การหารจะดำเนินต่อไป

d) หากการจ่ายเงินปันผลเป็นจำนวนเต็ม เมื่อหารด้วยเศษส่วนทศนิยม ก็จะเพิ่มขึ้นโดยการบวกศูนย์เข้าไป

ดังนั้น หากต้องการหารตัวเลขด้วยเศษส่วนทศนิยม คุณต้องทิ้งเครื่องหมายจุลภาคในตัวหาร แล้วเพิ่มเงินปันผลหลายเท่าเมื่อตัวหารเพิ่มขึ้นเมื่อทิ้งเครื่องหมายจุลภาคในนั้น แล้วจึงทำการหารตามกฎ สำหรับการหารเศษส่วนทศนิยมด้วยจำนวนเต็ม

§ 112 ผลหารโดยประมาณ

ในย่อหน้าก่อนหน้านี้ เราดูที่การหารเศษส่วนทศนิยม และในตัวอย่างทั้งหมดที่เราแก้ได้ การหารก็เสร็จสมบูรณ์ กล่าวคือ ได้ผลหารที่แน่นอน อย่างไรก็ตาม ในกรณีส่วนใหญ่ ไม่สามารถหาผลหารที่แน่นอนได้ ไม่ว่าเราจะหารต่อไปแค่ไหนก็ตาม ต่อไปนี้เป็นกรณีหนึ่ง: หาร 53 ด้วย 101

เราได้เลขผลหารมาแล้ว 5 หลัก แต่การหารยังไม่สิ้นสุดและหวังว่าจะไม่มีจุดสิ้นสุดเพราะส่วนที่เหลือเราเริ่มมีตัวเลขที่เคยเจอมาก่อน ในผลหารตัวเลขจะถูกทำซ้ำด้วย: เห็นได้ชัดว่าหลังจากหมายเลข 7 หมายเลข 5 จะปรากฏขึ้นตามด้วย 2 เป็นต้น อย่างไม่มีที่สิ้นสุด ในกรณีเช่นนี้ การหารจะถูกขัดจังหวะและจำกัดอยู่เพียงตัวเลขสองสามหลักแรกของผลหาร ผลหารนี้เรียกว่า คนใกล้ชิดเราจะแสดงพร้อมตัวอย่างวิธีการแบ่งส่วน

ปล่อยให้จำเป็นต้องหาร 25 ด้วย 3 แน่นอนว่าไม่สามารถหาผลหารที่แน่นอนซึ่งแสดงเป็นจำนวนเต็มหรือเศษส่วนทศนิยมจากการหารดังกล่าวได้ ดังนั้น เราจะหาผลหารโดยประมาณ:

25: 3 = 8 และเศษ 1

ผลหารโดยประมาณคือ 8; แน่นอนว่ามันน้อยกว่าผลหารที่แน่นอนเนื่องจากมีเศษ 1 เพื่อให้ได้ผลหารที่แน่นอนคุณต้องบวกเศษส่วนที่ได้รับโดยการหารเศษที่เหลือเท่ากับ 1 ด้วย 3 ให้กับผลหารโดยประมาณที่พบนั่นคือ , ถึง 8; นี่จะเป็นเศษส่วน 1/3. ซึ่งหมายความว่าผลหารที่แน่นอนจะแสดงเป็นจำนวนคละ 8 1/3 เนื่องจาก 1/3 แสดงถึง เศษส่วนที่ถูกต้องนั่นคือเศษส่วน น้อยกว่าหนึ่งแล้วทิ้งไปเราก็อนุญาต ข้อผิดพลาด, ที่ น้อยกว่าหนึ่ง- ผลหาร 8 จะเป็น ผลหารโดยประมาณจนถึงความสามัคคีกับข้อเสียถ้าแทนที่จะเป็น 8 เราเอา 9 มาเป็นผลหาร เราก็จะยอมให้มีข้อผิดพลาดที่น้อยกว่าหนึ่งด้วย เนื่องจากเราจะไม่บวกทั้งหน่วย แต่บวกด้วย 2/3 เจตจำนงส่วนตัวเช่นนี้ ผลหารโดยประมาณภายในหนึ่งที่มีส่วนเกิน

ตอนนี้เรามาดูอีกตัวอย่างหนึ่ง สมมติว่าเราต้องหาร 27 ด้วย 8 เนื่องจากเราจะไม่ได้ผลหารที่แน่นอนซึ่งแสดงเป็นจำนวนเต็ม เราจึงต้องหาผลหารโดยประมาณ:

27: 8 = 3 และเศษ 3

ที่นี่ข้อผิดพลาดเท่ากับ 3/8 ซึ่งน้อยกว่าหนึ่งซึ่งหมายความว่าผลหารโดยประมาณ (3) พบว่าแม่นยำกับอันที่มีข้อเสีย มาแบ่งกันต่อ: แบ่ง 3 ส่วนที่เหลือออกเป็นสิบ เราจะได้ 30 ในสิบ หารด้วย 8

เราได้ 3 ในด้านผลหาร แทนที่หนึ่งในสิบ และ 6 ในสิบของเศษ. หากเราจำกัดตัวเองไว้ที่หมายเลข 3.3 และทิ้งส่วนที่เหลือ 6 เราจะยอมให้มีข้อผิดพลาดน้อยกว่าหนึ่งในสิบ ทำไม เพราะจะได้ผลหารที่แน่นอนเมื่อเราบวกกับ 3.3 ผลลัพธ์ของการหาร 6 ในสิบด้วย 8 ส่วนนี้จะให้ผลตอบแทน 6/80 ซึ่งน้อยกว่าหนึ่งในสิบ (ตรวจสอบ!) ดังนั้น หากในผลหารเราจำกัดตัวเองไว้ที่สิบ เราก็สามารถพูดได้ว่าพบผลหารแล้ว แม่นถึงหนึ่งในสิบ(มีข้อเสีย).

ลองหารต่อไปเพื่อหาทศนิยมอีกตำแหน่งหนึ่ง เมื่อต้องการทำเช่นนี้ เราแบ่ง 6 ในสิบออกเป็นร้อยและรับ 60 ในร้อย หารด้วย 8

ในผลหารอันดับสามกลายเป็น 7 และส่วนที่เหลืออีก 4 ในร้อย ถ้าเราทิ้งมันไปเราจะยอมให้มีข้อผิดพลาดน้อยกว่าหนึ่งร้อยเพราะ 4 ในร้อยหารด้วย 8 นั้นน้อยกว่าหนึ่งร้อย ในกรณีเช่นนี้ พวกเขาบอกว่าพบผลหารแล้ว แม่นถึงร้อยเลย(มีข้อเสีย).

ในตัวอย่างที่เรากำลังดูอยู่ตอนนี้ เราสามารถหาผลหารที่แน่นอนซึ่งแสดงเป็นเศษส่วนทศนิยมได้ เมื่อต้องการทำเช่นนี้ ก็เพียงพอที่จะแบ่งเศษสุดท้าย 4 ในร้อย ออกเป็นพันและหารด้วย 8

อย่างไรก็ตาม ในกรณีส่วนใหญ่ ไม่สามารถหาผลหารที่แน่นอนได้ และต้องจำกัดตัวเองให้อยู่แค่ค่าโดยประมาณเท่านั้น ตอนนี้เราจะดูตัวอย่างนี้:

40: 7 = 5,71428571...

จุดที่อยู่ท้ายตัวเลขแสดงว่าการหารยังไม่สมบูรณ์ กล่าวคือ ความเท่าเทียมกันเป็นการประมาณ โดยปกติแล้วความเท่าเทียมกันโดยประมาณจะถูกเขียนดังนี้:

40: 7 = 5,71428571.

เราหาผลหารที่มีทศนิยมแปดตำแหน่ง แต่หากไม่ต้องการความแม่นยำอย่างมาก คุณสามารถจำกัดตัวเองให้เหลือเพียงส่วนของผลหารทั้งหมด เช่น หมายเลข 5 (หรือ 6 ที่แม่นยำยิ่งขึ้น) เพื่อความแม่นยำยิ่งขึ้น เราสามารถคำนึงถึงหนึ่งในสิบและหารผลหารเท่ากับ 5.7 หากความแม่นยำไม่เพียงพอด้วยเหตุผลบางประการ คุณสามารถหยุดที่หนึ่งในร้อยแล้วเอา 5.71 เป็นต้น มาเขียนผลหารแต่ละรายการแล้วตั้งชื่อกัน

ผลหารโดยประมาณอันแรกแม่นยำถึง 1 6

วินาที » » » ถึงหนึ่งในสิบ 5.7.

สาม » » » ถึงหนึ่งร้อย 5.71

ที่สี่ » » » ถึงหนึ่งพัน 5.714

ดังนั้น เพื่อที่จะหาผลหารโดยประมาณที่แม่นยำสำหรับบางคน เช่น ทศนิยมตำแหน่งที่ 3 (เช่น ไม่เกินหนึ่งพัน) ให้หยุดการหารทันทีที่พบเครื่องหมายนี้ ในกรณีนี้ คุณต้องจำกฎที่กำหนดไว้ในมาตรา 40

§ 113 ปัญหาที่ง่ายที่สุดเกี่ยวกับเปอร์เซ็นต์

หลังจากเรียนรู้เรื่องทศนิยมแล้ว เราจะมาแก้โจทย์ปัญหาเพิ่มอีก 2-3 เปอร์เซ็นต์

ปัญหาเหล่านี้คล้ายคลึงกับปัญหาที่เราแก้ไขในแผนกเศษส่วน แต่ตอนนี้เราจะเขียนเศษหนึ่งในร้อยในรูปของเศษส่วนทศนิยม กล่าวคือ โดยไม่มีตัวส่วนที่กำหนดไว้อย่างชัดเจน

ก่อนอื่น คุณต้องสามารถย้ายจากเศษส่วนธรรมดาไปเป็นทศนิยมที่มีตัวส่วนเป็น 100 ได้อย่างง่ายดาย เมื่อต้องการทำเช่นนี้ คุณต้องหารตัวเศษด้วยตัวส่วน:

ตารางด้านล่างแสดงวิธีที่ตัวเลขที่มีเครื่องหมาย % (เปอร์เซ็นต์) ถูกแทนที่ด้วยเศษส่วนทศนิยมที่มีตัวส่วนเป็น 100:

ให้เราพิจารณาปัญหาหลายประการ

1. การหาเปอร์เซ็นต์ หมายเลขที่กำหนด.

ภารกิจที่ 1หมู่บ้านหนึ่งมีประชากรเพียง 1,600 คน จำนวนบุตร วัยเรียนคิดเป็น 25% ของจำนวนผู้อยู่อาศัยทั้งหมด หมู่บ้านนี้มีเด็กวัยเรียนกี่คน?

ในปัญหานี้ คุณต้องหา 25% หรือ 0.25 ของ 1,600 ปัญหาได้รับการแก้ไขโดยการคูณ:

1,600 0.25 = 400 (เด็ก)

ดังนั้น 25% ของ 1,600 คือ 400

เพื่อให้เข้าใจงานนี้อย่างชัดเจน ควรระลึกไว้ว่าทุกๆ ร้อยประชากรจะมีเด็กวัยเรียน 25 คน ดังนั้น หากต้องการหาจำนวนเด็กวัยเรียนทั้งหมด คุณต้องทราบก่อนว่าจำนวน 1,600 (16) มีกี่ร้อยคน แล้วจึงคูณ 25 ด้วยจำนวนร้อย (25 x 16 = 400) วิธีนี้ทำให้คุณสามารถตรวจสอบความถูกต้องของโซลูชันได้

ภารกิจที่ 2ธนาคารออมสินให้ผลตอบแทนแก่ผู้ฝากเงิน 2% ต่อปี ผู้ฝากเงินจะได้รับรายได้เท่าใดในหนึ่งปีหากเขาใส่ไว้ในเครื่องบันทึกเงินสด: ก) 200 รูเบิล? b) 500 รูเบิล? ค) 750 รูเบิล? ง) 1,000 รูเบิล?

ในทั้งสี่กรณี เพื่อแก้ปัญหา คุณจะต้องคำนวณ 0.02 ของจำนวนเงินที่ระบุ เช่น แต่ละตัวเลขเหล่านี้จะต้องคูณด้วย 0.02 มาทำกัน:

ก) 200 · 0.02 = 4 (ถู)

b) 500 · 0.02 = 10 (ถู)

c) 750 0.02 = 15 (ถู.)

ง) 1,000 · 0.02 = 20 (รูเบิล)

แต่ละกรณีเหล่านี้สามารถตรวจสอบได้โดยการพิจารณาดังต่อไปนี้ ธนาคารออมสินให้ผลตอบแทนแก่ผู้ฝาก 2% คือ 0.02 ของจำนวนเงินที่ฝาก หากจำนวนคือ 100 รูเบิล ดังนั้น 0.02 ของมันจะเป็น 2 รูเบิล ซึ่งหมายความว่าทุก ๆ ร้อยจะนำนักลงทุนมา 2 รูเบิล รายได้. ดังนั้นในแต่ละกรณีที่พิจารณาก็เพียงพอที่จะทราบว่ามีกี่ร้อยในจำนวนที่กำหนดและคูณ 2 รูเบิลด้วยจำนวนร้อยนี้ ในตัวอย่าง ก) มี 2 ร้อย ซึ่งหมายถึง

2 2 = 4 (ถู)

ในตัวอย่าง ง) มี 10 ร้อย ซึ่งหมายถึง

2 10 = 20 (ถู)

2. ค้นหาตัวเลขตามเปอร์เซ็นต์

ภารกิจที่ 1โรงเรียนสำเร็จการศึกษานักเรียน 54 คนในฤดูใบไม้ผลิ คิดเป็น 6% ของการลงทะเบียนทั้งหมด ปีที่แล้วมีนักเรียนกี่คนในโรงเรียน? ปีการศึกษา?

ให้เราอธิบายความหมายของงานนี้ก่อน โรงเรียนสำเร็จการศึกษาจำนวน 54 คน ซึ่งคิดเป็น 6% ของจำนวนนักเรียนทั้งหมด หรืออีกนัยหนึ่งคือ 6 ในร้อย (0.06) ของนักเรียนทั้งหมดในโรงเรียน ซึ่งหมายความว่าเรารู้ส่วนของนักเรียนที่แสดงด้วยตัวเลข (54) และเศษส่วน (0.06) และจากเศษส่วนนี้เราจะต้องค้นหาจำนวนทั้งหมด ดังนั้นเราจึงมีงานธรรมดาต่อหน้าเราในการค้นหาตัวเลขจากเศษส่วน (§90, ย่อหน้าที่ 6) ปัญหาประเภทนี้ได้รับการแก้ไขโดยการแบ่ง:

ซึ่งหมายความว่ามีนักเรียนเพียง 900 คนในโรงเรียน

การตรวจสอบปัญหาดังกล่าวโดยการแก้ปัญหาผกผันจะมีประโยชน์ เช่น หลังจากแก้ไขปัญหาแล้ว อย่างน้อยคุณควรแก้ไขปัญหาประเภทแรกในหัว (ค้นหาเปอร์เซ็นต์ของตัวเลขที่กำหนด): หาจำนวนที่พบ ( 900) ตามที่กำหนดและหาเปอร์เซ็นต์ที่ระบุในปัญหาที่แก้ไขแล้ว ได้แก่:

900 0,06 = 54.

ภารกิจที่ 2ครอบครัวใช้จ่ายเงิน 780 รูเบิลเป็นค่าอาหารในระหว่างเดือน ซึ่งคิดเป็น 65% ของรายได้ต่อเดือนของพ่อ กำหนดรายได้ต่อเดือนของเขา

งานนี้มีความหมายเหมือนกับงานก่อนหน้า ให้ส่วนหนึ่งของรายได้ต่อเดือนแสดงเป็นรูเบิล (780 รูเบิล) และระบุว่าส่วนนี้คือ 65% หรือ 0.65 ของรายได้ทั้งหมด และสิ่งที่คุณกำลังมองหาคือรายได้ทั้งหมด:

780: 0,65 = 1 200.

ดังนั้นรายได้ที่ต้องการคือ 1,200 รูเบิล

3. การหาเปอร์เซ็นต์ของตัวเลข

ภารกิจที่ 1ใน ห้องสมุดโรงเรียนมีเพียง 6,000 เล่มเท่านั้น ในจำนวนนี้มีหนังสือเกี่ยวกับคณิตศาสตร์จำนวน 1,200 เล่ม หนังสือคณิตศาสตร์คิดเป็นกี่เปอร์เซ็นต์ของจำนวนหนังสือทั้งหมดในห้องสมุด?

เราได้พิจารณาปัญหาประเภทนี้แล้ว (§97) และได้ข้อสรุปว่าในการคำนวณเปอร์เซ็นต์ของตัวเลขสองตัว คุณต้องค้นหาอัตราส่วนของตัวเลขเหล่านี้แล้วคูณด้วย 100

ในโจทย์ของเรา เราจำเป็นต้องค้นหาอัตราส่วนเปอร์เซ็นต์ของตัวเลข 1,200 และ 6,000

ขั้นแรกให้หาอัตราส่วนแล้วคูณด้วย 100:

ดังนั้น เปอร์เซ็นต์ของตัวเลข 1,200 และ 6,000 คือ 20 กล่าวอีกนัยหนึ่ง หนังสือคณิตศาสตร์คิดเป็น 20% ของจำนวนหนังสือทั้งหมด

ในการตรวจสอบ เรามาแก้ปัญหาผกผันกัน: หา 20% ของ 6,000:

6 000 0,2 = 1 200.

ภารกิจที่ 2โรงงานควรได้รับถ่านหิน 200 ตัน มีการส่งมอบถ่านหินจำนวน 80 ตันให้กับโรงงานแล้วกี่เปอร์เซ็นต์?

ปัญหานี้ถามว่าตัวเลขหนึ่ง (80) เป็นเปอร์เซ็นต์ของอีกจำนวนหนึ่ง (200) อัตราส่วนของตัวเลขเหล่านี้จะเท่ากับ 80/200 ลองคูณด้วย 100:

ซึ่งหมายความว่ามีการส่งมอบถ่านหินไปแล้ว 40%

การคูณทศนิยมเกิดขึ้นในสามขั้นตอน

เศษส่วนทศนิยมจะถูกเขียนในคอลัมน์และคูณเหมือนตัวเลขธรรมดา

เรานับจำนวนตำแหน่งทศนิยมสำหรับเศษส่วนทศนิยมตัวแรกและตัวที่สอง เราบวกหมายเลขของพวกเขา

จากผลลัพธ์ที่ได้ เรานับจากขวาไปซ้ายตามจำนวนตัวเลขเดียวกันกับที่เราได้รับในย่อหน้าด้านบนและใส่ลูกน้ำ

วิธีการคูณทศนิยม

เขียนเศษส่วนทศนิยมลงในคอลัมน์แล้วคูณเป็น จำนวนเต็มโดยไม่สนใจเครื่องหมายจุลภาค นั่นคือเราถือว่า 3.11 เป็น 311 และ 0.01 เป็น 1

เราได้รับ 311. ตอนนี้เรานับจำนวนเครื่องหมาย (หลัก) หลังจุดทศนิยมของเศษส่วนทั้งสอง ทศนิยมตัวแรกมีสองหลักและที่สองมีสองหลัก จำนวนตำแหน่งทศนิยมทั้งหมด:

เรานับจากขวาไปซ้าย 4 เครื่องหมาย (หลัก) ของจำนวนผลลัพธ์ ผลลัพธ์ที่ได้มีตัวเลขน้อยกว่าที่ต้องคั่นด้วยลูกน้ำ ในกรณีนี้คุณต้องการ ซ้ายเพิ่มจำนวนศูนย์ที่หายไป

เราขาดไปหนึ่งหลัก ดังนั้นเราจึงบวกหนึ่งศูนย์ทางด้านซ้าย

เมื่อคูณเศษส่วนทศนิยมใดๆวันที่ 10; 100; 1,000 ฯลฯ จุดทศนิยมจะเลื่อนไปทางขวาตามตำแหน่งที่มีศูนย์อยู่หลังจุดทศนิยม

70.1 10 = 701

0.023 100 = 2.3

5.6 · 1,000 = 5,600

หากต้องการคูณทศนิยมด้วย 0.1; 0.01; 0.001 เป็นต้น คุณต้องย้ายจุดทศนิยมในเศษส่วนนี้ไปทางซ้ายให้มากที่สุดเท่าที่มีศูนย์อยู่ข้างหน้าจุดนั้น

เรานับแม้กระทั่งศูนย์!

• 12 0.1 = 1.2
• 0.05 · 0.1 = 0.005
• 1.256 · 0.01 = 0.012 56

เพื่อให้เข้าใจวิธีการคูณทศนิยม มาดูตัวอย่างกัน

กฎสำหรับการคูณทศนิยม

1) คูณโดยไม่ต้องสนใจเครื่องหมายจุลภาค

2) ด้วยเหตุนี้ เราจึงแยกตัวเลขหลังจุดทศนิยมได้มากเท่ากับจำนวนหลักหลังจุดทศนิยมในทั้งสองตัวรวมกัน

ค้นหาผลคูณของเศษส่วนทศนิยม:

ในการคูณเศษส่วนทศนิยม เราจะคูณโดยไม่ต้องสนใจเครื่องหมายลูกน้ำ นั่นคือเราไม่ได้คูณ 6.8 และ 3.4 แต่เป็น 68 และ 34 ด้วยเหตุนี้เราจึงแยกตัวเลขหลังจุดทศนิยมได้มากเท่าที่มีหลังจุดทศนิยมในทั้งสองตัวรวมกัน ตัวประกอบแรกจะมีหนึ่งหลักหลังจุดทศนิยม ส่วนตัวที่สองก็มีหนึ่งตัวด้วย โดยรวมแล้ว เราแยกตัวเลขสองตัวหลังจุดทศนิยม ดังนั้นเราจึงได้คำตอบสุดท้าย: 6.8∙3.4=23.12

เราคูณทศนิยมโดยไม่คำนึงถึงจุดทศนิยม ที่จริงแล้ว แทนที่จะคูณ 36.85 ด้วย 1.14 เรากลับคูณ 3685 ด้วย 14 เราได้ 51590 ตอนนี้ในผลลัพธ์นี้ เราจำเป็นต้องแยกตัวเลขให้มากที่สุดเท่าที่จะเป็นไปได้ด้วยลูกน้ำ เนื่องจากทั้งสองตัวประกอบกัน ตัวเลขตัวแรกมีตัวเลขสองหลักหลังจุดทศนิยม ตัวที่สองมีหนึ่งตัว โดยรวมแล้วเราคั่นตัวเลขสามหลักด้วยลูกน้ำ เนื่องจากมีศูนย์อยู่หลังจุดทศนิยมที่ส่วนท้ายของรายการ เราจึงไม่เขียนลงในคำตอบ: 36.85∙1.4=51.59

หากต้องการคูณทศนิยมเหล่านี้ ให้คูณตัวเลขโดยไม่ต้องสนใจเครื่องหมายจุลภาค นั่นคือเราคูณจำนวนธรรมชาติ 2315 และ 7 เราได้ 16205 ในจำนวนนี้ คุณต้องแยกตัวเลขสี่หลักหลังจุดทศนิยม - ให้มากที่สุดเท่าที่มีทั้งสองตัวประกอบกัน (สองตัวในแต่ละตัว) คำตอบสุดท้าย: 23.15∙0.07=1.6205

การคูณเศษส่วนทศนิยมด้วยจำนวนธรรมชาติก็ทำในลักษณะเดียวกัน เราคูณตัวเลขโดยไม่ต้องสนใจเครื่องหมายจุลภาคนั่นคือเราคูณ 75 ด้วย 16 ผลลัพธ์ที่ได้ควรมีจำนวนเครื่องหมายหลังจุดทศนิยมเท่ากันเนื่องจากมีทั้งสองปัจจัยรวมกัน - หนึ่ง ดังนั้น 75∙1.6=120.0=120

เราเริ่มคูณเศษส่วนทศนิยมด้วยการคูณจำนวนธรรมชาติ เนื่องจากเราไม่ได้สนใจเครื่องหมายจุลภาค หลังจากนี้เราจะแยกตัวเลขหลังจุดทศนิยมให้มากที่สุดตามที่มีตัวประกอบทั้งสองอยู่รวมกัน ตัวเลขตัวแรกมีทศนิยมสองตำแหน่ง ตัวที่สองก็มีทศนิยมสองตำแหน่งด้วย โดยรวมแล้ว ผลลัพธ์ควรเป็นตัวเลขสี่หลักหลังจุดทศนิยม: 4.72∙5.04=23.7888

และอีกสองสามตัวอย่างเกี่ยวกับการคูณเศษส่วนทศนิยม:

www.for6cl.uznateshe.ru

การคูณทศนิยม กฎ ตัวอย่าง วิธีแก้

มาดูการกระทำต่อไปกับเศษส่วนทศนิยมกันดีกว่า ตอนนี้เราจะมาดูแบบครอบคลุมกัน การคูณทศนิยม- มาคุยกันก่อน หลักการทั่วไปการคูณเศษส่วนทศนิยม หลังจากนี้ เราจะไปยังการคูณเศษส่วนทศนิยมด้วยเศษส่วนทศนิยม เราจะแสดงวิธีคูณเศษส่วนทศนิยมด้วยคอลัมน์ และเราจะพิจารณาวิธีแก้ตัวอย่าง ต่อไป เราจะดูการคูณเศษส่วนทศนิยมด้วยจำนวนธรรมชาติ โดยเฉพาะ 10, 100 เป็นต้น สุดท้ายนี้ เรามาพูดถึงการคูณทศนิยมด้วยเศษส่วนและจำนวนคละกัน

สมมติว่าในบทความนี้เราจะพูดถึงการคูณเศษส่วนทศนิยมที่เป็นบวกเท่านั้น (ดูค่าบวกและ ตัวเลขติดลบ- กรณีอื่น ๆ จะมีการกล่าวถึงในบทความ การคูณ สรุปตัวเลขและ การคูณจำนวนจริง.

การนำทางหน้า

หลักการทั่วไปของการคูณทศนิยม

เรามาพูดถึงหลักการทั่วไปที่ควรปฏิบัติเมื่อคูณด้วยทศนิยม

เนื่องจากทศนิยมจำกัดและเศษส่วนคาบไม่สิ้นสุดเป็นรูปแบบทศนิยมของเศษส่วนร่วม การคูณทศนิยมจึงเท่ากับการคูณเศษส่วนร่วม กล่าวอีกนัยหนึ่ง การคูณทศนิยมที่มีขอบเขตจำกัด, การคูณเศษส่วนทศนิยมที่มีขอบเขตจำกัดและเป็นงวด, และ การคูณทศนิยมเป็นระยะลงมาเป็นการคูณเศษส่วนสามัญหลังจากแปลงเศษส่วนทศนิยมเป็นเศษส่วนสามัญแล้ว

ลองดูตัวอย่างการใช้หลักการคูณเศษส่วนทศนิยมที่ระบุไว้

คูณทศนิยม 1.5 และ 0.75

ให้เราแทนที่เศษส่วนทศนิยมที่คูณด้วยเศษส่วนสามัญที่สอดคล้องกัน เนื่องจาก 1.5=15/10 และ 0.75=75/100 ดังนั้น คุณสามารถลดเศษส่วนแล้วเลือกทั้งส่วนได้ เศษส่วนเกินและสะดวกกว่าถ้าเขียนเศษส่วนสามัญผลลัพธ์ 1 125/1 000 เป็นเศษส่วนทศนิยม 1.125

ควรสังเกตว่าการคูณเศษส่วนทศนิยมสุดท้ายในคอลัมน์นั้นสะดวก เราจะพูดถึงวิธีการคูณเศษส่วนทศนิยมนี้ในย่อหน้าถัดไป

ลองดูตัวอย่างการคูณเศษส่วนทศนิยมเป็นงวด

คำนวณผลคูณของเศษส่วนทศนิยมเป็นงวด 0,(3) และ 2,(36) .

ลองแปลงเศษส่วนทศนิยมเป็นงวดเป็นเศษส่วนสามัญ:

แล้ว. คุณสามารถแปลงเศษส่วนสามัญที่ได้ให้เป็นเศษส่วนทศนิยมได้:


หากในบรรดาเศษส่วนทศนิยมที่คูณแล้วนั้นมีเศษส่วนที่ไม่เป็นงวดเป็นอนันต์ เศษส่วนที่คูณทั้งหมดรวมทั้งเศษส่วนที่มีขอบเขตและเศษส่วนควรถูกปัดเศษให้เป็นตัวเลขที่แน่นอน (ดู การปัดเศษตัวเลข) แล้วคูณเศษส่วนทศนิยมสุดท้ายที่ได้รับหลังจากการปัดเศษ

คูณทศนิยม 5.382... และ 0.2

ขั้นแรก ลองปัดเศษทศนิยมที่ไม่ใช่คาบเป็นอนันต์ก่อน โดยปัดเศษให้เป็นทศนิยมได้ เราได้ 5.382...ก็คือ5.38 เศษส่วนทศนิยมสุดท้าย 0.2 ไม่จำเป็นต้องปัดเศษให้เป็นทศนิยมที่ใกล้ที่สุด ดังนั้น 5.382...·0.2ความลับ5.38·0.2 ยังคงต้องคำนวณผลคูณของเศษส่วนทศนิยมสุดท้าย: 5.38·0.2=538/100·2/10= 1,076/1,000=1.076

การคูณเศษส่วนทศนิยมตามคอลัมน์

การคูณเศษส่วนทศนิยมที่มีขอบเขตจำกัดสามารถทำได้ในคอลัมน์เดียว คล้ายกับการคูณจำนวนธรรมชาติในคอลัมน์

มากำหนดกัน กฎสำหรับการคูณเศษส่วนทศนิยมตามคอลัมน์- หากต้องการคูณเศษส่วนทศนิยมตามคอลัมน์ คุณต้อง:

• โดยไม่ต้องสนใจลูกน้ำให้ทำการคูณตามกฎการคูณทั้งหมดด้วยคอลัมน์ของจำนวนธรรมชาติ
• แยกจากหมายเลขผลลัพธ์ จุดทศนิยมมีจำนวนหลักทางด้านขวาเท่ากับมีทศนิยมในทั้งสองปัจจัยรวมกัน และหากผลคูณมีตัวเลขไม่เพียงพอ ก็จะต้องบวกจำนวนศูนย์ที่ต้องการทางด้านซ้าย

ลองดูตัวอย่างการคูณเศษส่วนทศนิยมตามคอลัมน์

คูณทศนิยม 63.37 และ 0.12

ลองคูณเศษส่วนทศนิยมในคอลัมน์กัน ขั้นแรก เราคูณตัวเลข โดยไม่สนใจเครื่องหมายจุลภาค:


สิ่งที่เหลืออยู่คือการเพิ่มลูกน้ำให้กับผลิตภัณฑ์ผลลัพธ์ เธอต้องแยกตัวเลข 4 หลักไปทางขวา เนื่องจากตัวประกอบมีทศนิยมทั้งหมด 4 ตำแหน่ง (2 หลักในเศษส่วน 3.37 และ 2 หลักในเศษส่วน 0.12) มีตัวเลขเพียงพอแล้ว คุณจึงไม่ต้องบวกเลขศูนย์ทางด้านซ้าย มาจบการบันทึกกันเถอะ:


ผลลัพธ์ที่ได้คือ 3.37·0.12=7.6044

คำนวณผลคูณทศนิยม 3.2601 และ 0.0254

เมื่อทำการคูณในคอลัมน์โดยไม่ต้องคำนึงถึงเครื่องหมายจุลภาค เราจะได้ภาพต่อไปนี้:


ตอนนี้ในผลิตภัณฑ์คุณต้องแยกตัวเลข 8 หลักทางด้านขวาด้วยเครื่องหมายจุลภาคเนื่องจากจำนวนตำแหน่งทศนิยมทั้งหมดของเศษส่วนที่คูณคือแปด แต่ในผลิตภัณฑ์มีเพียง 7 หลัก ดังนั้นคุณต้องเพิ่มเลขศูนย์ทางด้านซ้ายให้มากที่สุดเท่าที่จะเป็นไปได้เพื่อแยกตัวเลข 8 หลักด้วยลูกน้ำ ในกรณีของเรา เราต้องกำหนดศูนย์สองตัว:


ซึ่งจะทำให้การคูณเศษส่วนทศนิยมตามคอลัมน์เสร็จสมบูรณ์

การคูณทศนิยมด้วย 0.1, 0.01 เป็นต้น

บ่อยครั้งคุณต้องคูณเศษส่วนทศนิยมด้วย 0.1, 0.01 และอื่นๆ ดังนั้นจึงแนะนำให้กำหนดกฎสำหรับการคูณเศษส่วนทศนิยมด้วยตัวเลขเหล่านี้ซึ่งเป็นไปตามหลักการคูณเศษส่วนทศนิยมที่กล่าวถึงข้างต้น

ดังนั้น, การคูณทศนิยมที่กำหนดด้วย 0.1, 0.01, 0.001 และอื่นๆให้เศษส่วนที่ได้รับจากต้นฉบับหากเครื่องหมายจุลภาคถูกย้ายไปทางซ้าย 1, 2, 3 และตัวเลขอื่น ๆ ตามลำดับและหากมีตัวเลขไม่เพียงพอที่จะย้ายเครื่องหมายจุลภาคคุณจะต้อง เพิ่มจำนวนศูนย์ที่ต้องการทางด้านซ้าย

ตัวอย่างเช่น หากต้องการคูณเศษส่วนทศนิยม 54.34 ด้วย 0.1 คุณต้องย้ายจุดทศนิยมในเศษส่วน 54.34 ไปทางซ้าย 1 หลัก ซึ่งจะให้เศษส่วน 5.434 ซึ่งก็คือ 54.34·0.1=5.434 ลองยกตัวอย่างอื่น คูณเศษส่วนทศนิยม 9.3 ด้วย 0.0001 เมื่อต้องการทำเช่นนี้ เราจำเป็นต้องย้ายจุดทศนิยม 4 หลักไปทางซ้ายในเศษส่วนทศนิยมคูณ 9.3 แต่สัญลักษณ์ของเศษส่วน 9.3 ไม่มีตัวเลขจำนวนมากขนาดนั้น ดังนั้นเราจึงต้องกำหนดศูนย์หลายๆ ตัวทางด้านซ้ายของเศษส่วน 9.3 เพื่อที่เราจะได้เลื่อนจุดทศนิยมไปเป็น 4 หลักได้อย่างง่ายดาย เราได้ 9.3·0.0001=0.00093

โปรดทราบว่ากฎที่ระบุไว้สำหรับการคูณเศษส่วนทศนิยมด้วย 0.1, 0.01, ... ก็ใช้ได้กับเศษส่วนทศนิยมอนันต์เช่นกัน ตัวอย่างเช่น 0.(18)·0.01=0.00(18) หรือ 93.938…·0.1=9.3938…

การคูณทศนิยมด้วยจำนวนธรรมชาติ

ที่แกนกลางของมัน การคูณทศนิยมด้วยจำนวนธรรมชาติไม่ต่างจากการคูณทศนิยมด้วยทศนิยม

วิธีที่สะดวกที่สุดในการคูณเศษส่วนทศนิยมสุดท้ายด้วยจำนวนธรรมชาติในคอลัมน์ ในกรณีนี้ คุณควรปฏิบัติตามกฎสำหรับการคูณเศษส่วนทศนิยมในคอลัมน์ที่กล่าวถึงในย่อหน้าใดย่อหน้าหนึ่ง

คำนวณผลคูณ 15·2.27

ลองคูณจำนวนธรรมชาติด้วยเศษส่วนทศนิยมในคอลัมน์:


เมื่อคูณเศษส่วนทศนิยมเป็นคาบด้วยจำนวนธรรมชาติ เศษส่วนคาบควรถูกแทนที่ด้วยเศษส่วนสามัญ

คูณเศษส่วนทศนิยม 0.(42) ด้วยจำนวนธรรมชาติ 22

ขั้นแรก เรามาแปลงเศษส่วนทศนิยมเป็นงวดให้เป็นเศษส่วนธรรมดา:

ทีนี้มาคูณกัน: . ผลลัพธ์นี้เป็นทศนิยมคือ 9,(3)

และเมื่อคูณเศษส่วนทศนิยมที่ไม่ใช่คาบเป็นอนันต์ด้วยจำนวนธรรมชาติ คุณต้องทำการปัดเศษก่อน

คูณ 4·2.145….

เมื่อปัดเศษทศนิยมอนันต์ดั้งเดิมให้เป็นทศนิยมแล้ว เราก็จะได้การคูณของจำนวนธรรมชาติและเศษส่วนทศนิยมสุดท้าย เรามี 4·2.145…µ4·2.15=8.60

การคูณทศนิยมด้วย 10, 100, …

บ่อยครั้งที่คุณต้องคูณเศษส่วนทศนิยมด้วย 10, 100, ... ดังนั้นจึงขอแนะนำให้พิจารณากรณีเหล่านี้อย่างละเอียด

มาออกเสียงกันเถอะ กฎสำหรับการคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 เป็นต้นเมื่อคูณเศษส่วนทศนิยมด้วย 10, 100, ... ในสัญกรณ์คุณจะต้องย้ายจุดทศนิยมไปทางขวาเป็น 1, 2, 3, ... หลักตามลำดับและทิ้งศูนย์พิเศษทางด้านซ้าย หากสัญลักษณ์ของเศษส่วนที่คูณมีตัวเลขไม่เพียงพอที่จะย้ายจุดทศนิยมคุณจะต้องเพิ่มจำนวนศูนย์ที่ต้องการทางด้านขวา

คูณเศษส่วนทศนิยม 0.0783 ด้วย 100

ลองเลื่อนเศษส่วน 0.0783 ไปทางขวาสองหลัก แล้วเราจะได้ 007.83 การปล่อยศูนย์สองตัวทางด้านซ้ายจะได้เศษส่วนทศนิยม 7.38 ดังนั้น 0.0783·100=7.83

คูณเศษส่วนทศนิยม 0.02 ด้วย 10,000

หากต้องการคูณ 0.02 ด้วย 10,000 เราต้องย้ายจุดทศนิยม 4 หลักไปทางขวา แน่นอนว่าเศษส่วน 0.02 มีตัวเลขไม่เพียงพอที่จะเลื่อนจุดทศนิยมไป 4 หลัก ดังนั้นเราจะบวกเลขศูนย์สองสามตัวทางด้านขวาเพื่อให้สามารถย้ายจุดทศนิยมได้ ในตัวอย่างของเรา แค่เพิ่มศูนย์สามตัวก็เพียงพอแล้ว เรามี 0.02000 หลังจากย้ายเครื่องหมายจุลภาค เราจะได้รายการ 00200.0 ทิ้งศูนย์ทางด้านซ้าย เราจะได้ตัวเลข 200.0 ซึ่งเท่ากับจำนวนธรรมชาติ 200 ซึ่งเป็นผลมาจากการคูณเศษส่วนทศนิยม 0.02 ด้วย 10,000

กฎที่ระบุไว้ก็เป็นจริงเช่นกันสำหรับการคูณเศษส่วนทศนิยมอนันต์ด้วย 10, 100, ... เมื่อคูณเศษส่วนทศนิยมเป็นงวด คุณต้องระวังช่วงเวลาของเศษส่วนที่เป็นผลมาจากการคูณ

คูณเศษส่วนทศนิยมเป็นงวด 5.32(672) ด้วย 1,000

ก่อนที่จะคูณ ให้เขียนเศษส่วนทศนิยมเป็นงวดเป็น 5.32672672672... ซึ่งจะช่วยให้เราหลีกเลี่ยงข้อผิดพลาดได้ ตอนนี้ย้ายลูกน้ำไปทางขวา 3 ตำแหน่ง เรามี 5 326.726726…. ดังนั้น หลังจากการคูณ จะได้เศษส่วนทศนิยมเป็นงวด 5 326,(726)

5.32(672)·1,000=5,326,(726) .

เมื่อคูณเศษส่วนที่ไม่ใช่คาบเป็นอนันต์ด้วย 10, 100, ... คุณต้องปัดเศษเศษส่วนอนันต์ให้เป็นตัวเลขจำนวนหนึ่งก่อน แล้วจึงทำการคูณ

การคูณทศนิยมด้วยเศษส่วนหรือจำนวนคละ

หากต้องการคูณเศษส่วนทศนิยมจำกัดหรือเศษส่วนทศนิยมเป็นงวดอนันต์ด้วยเศษส่วนร่วมหรือจำนวนผสม คุณต้องแสดงเศษส่วนทศนิยมให้เป็นเศษส่วนร่วม แล้วจึงทำการคูณ

คูณเศษส่วนทศนิยม 0.4 ด้วยจำนวนคละ

ตั้งแต่ 0.4=4/10=2/5 แล้ว จำนวนผลลัพธ์สามารถเขียนเป็นเศษส่วนทศนิยมเป็นระยะ 1.5(3)

เมื่อคูณเศษส่วนทศนิยมที่ไม่ใช่คาบเป็นอนันต์ด้วยเศษส่วนหรือจำนวนคละ ให้แทนที่เศษส่วนหรือจำนวนคละด้วยเศษส่วนทศนิยม จากนั้นปัดเศษเศษส่วนที่คูณแล้วจึงเสร็จสิ้นการคำนวณ

เนื่องจาก 2/3=0.6666...แล้ว หลังจากปัดเศษเศษส่วนที่คูณแล้วให้เป็นส่วนหนึ่งในพัน เราจะได้ผลลัพธ์ของเศษส่วนทศนิยมสองตัวสุดท้ายคือ 3.568 และ 0.667 มาทำการคูณแบบเรียงเป็นแนว:


ผลลัพธ์ที่ได้ควรถูกปัดเศษให้เป็นจำนวนหนึ่งในพันที่ใกล้ที่สุด เนื่องจากเศษส่วนที่คูณนั้นถูกต้องแม่นยำถึงหลักพัน เราจึงได้ 2.379856µ2.380

www.cleverstudents.ru

29. การคูณทศนิยม กฎ




หาพื้นที่ของสี่เหลี่ยมที่มีด้านเท่ากัน
1.4 ซม. และ 0.3 ซม. ลองแปลงเดซิเมตรเป็นเซนติเมตร:

1.4 เดซิเมตร = 14 ซม. 0.3 เดซิเมตร = 3 ซม.

ทีนี้ลองคำนวณพื้นที่เป็นเซนติเมตรกัน

เอส = 14 3 = 42 ซม. 2

แปลงตารางเซนติเมตรเป็นตารางเซนติเมตร
เดซิเมตร:

วัน ม 2 = 0.42 วัน ม 2

ซึ่งหมายความว่า S = 1.4 dm 0.3 dm = 0.42 dm 2

การคูณเศษส่วนทศนิยมสองตัวทำได้ดังนี้:
1) คูณตัวเลขโดยไม่ต้องคำนึงถึงลูกน้ำ
2) วางเครื่องหมายจุลภาคในผลิตภัณฑ์เพื่อแยกออกทางด้านขวา
จำนวนเครื่องหมายเท่ากันซึ่งแยกจากทั้งสองปัจจัย
รวมกัน ตัวอย่างเช่น:

1,1 0,2 = 0,22 ; 1,1 1,1 = 1,21 ; 2,2 0,1 = 0,22 .

ตัวอย่างการคูณเศษส่วนทศนิยมในคอลัมน์:



แทนที่จะคูณตัวเลขใดๆ ด้วย 0.1; 0.01; 0.001
คุณสามารถหารตัวเลขนี้ด้วย 10; 100 ; หรือ 1,000 ตามลำดับ
ตัวอย่างเช่น:

22 0,1 = 2,2 ; 22: 10 = 2,2 .

เมื่อคูณเศษส่วนทศนิยมด้วยจำนวนธรรมชาติ เราต้อง:

1) คูณตัวเลขโดยไม่ต้องสนใจเครื่องหมายจุลภาค

2) ในผลลัพธ์ที่ได้ ให้วางลูกน้ำไว้ทางด้านขวา
มันมีจำนวนหลักเท่ากับเศษส่วนทศนิยม

มาหาสินค้ากัน 3.12 10. ตามกฎข้างต้น
ก่อนอื่นเราคูณ 312 ด้วย 10 เราได้รับ: 312 10 = 3120
ตอนนี้เราแยกตัวเลขสองหลักทางด้านขวาด้วยลูกน้ำและรับ:

3,12 10 = 31,20 = 31,2 .

ซึ่งหมายความว่าเมื่อคูณ 3.12 ด้วย 10 เราจะย้ายจุดทศนิยมไปหนึ่งจุด
หมายเลขทางด้านขวา ถ้าเราคูณ 3.12 ด้วย 100 เราจะได้ 312 นั่นก็คือ
ลูกน้ำถูกย้ายไปทางขวาสองหลัก

3,12 100 = 312,00 = 312 .

เมื่อคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 ฯลฯ คุณต้องมี
ในส่วนนี้ให้เลื่อนจุดทศนิยมไปทางขวาตามจำนวนตำแหน่งที่มีศูนย์
มีค่าตัวคูณ ตัวอย่างเช่น:

0,065 1000 = 0065, = 65 ;

2,9 1000 = 2,900 1000 = 2900, = 2900 .

ปัญหาในหัวข้อ “การคูณทศนิยม”

school-assistant.ru

การบวก ลบ คูณ และหารทศนิยม

การบวกและการลบทศนิยมจะคล้ายกับการบวกและการลบจำนวนธรรมชาติ แต่มีเงื่อนไขบางประการ

กฎ. ดำเนินการโดยใช้ตัวเลขของจำนวนเต็มและเศษส่วนเป็นตัวเลขธรรมชาติ

ในการเขียน การบวกและการลบทศนิยมเครื่องหมายจุลภาคที่แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนควรอยู่ที่การบวกและผลรวมหรือที่เครื่องหมายลบ การลบและความแตกต่างในคอลัมน์เดียว (เครื่องหมายจุลภาคใต้เครื่องหมายจุลภาคจากการเขียนเงื่อนไขจนถึงจุดสิ้นสุดของการคำนวณ)

การบวกและการลบทศนิยมไปที่บรรทัด:

243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651

843,217 - 700,628 = (800 - 700) + 40 + 3 + (0,2 - 0,6) + (0,01 - 0,02) + (0,007 - 0,008) = 100 + 40 + 2 + (1,2 - 0,6) + (0,01 - 0,02) + (0,007 - 0,008) = 100 + 40 + 2 + 0,5 + (0,11 - 0,02) + (0,007 - 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 - 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 - 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589

การบวกและการลบทศนิยมในคอลัมน์:

การบวกทศนิยมต้องมีบรรทัดบนเพิ่มเติมเพื่อบันทึกตัวเลขเมื่อผลรวมของค่าตำแหน่งเกินสิบ การลบทศนิยมต้องมีบรรทัดบนเพิ่มเติมเพื่อระบุตำแหน่งที่ยืม 1

หากมีตัวเลขไม่เพียงพอของส่วนที่เป็นเศษส่วนทางด้านขวาของส่วนบวกหรือส่วนลบจากนั้นทางด้านขวาในส่วนที่เป็นเศษส่วนคุณสามารถเพิ่มศูนย์ได้มากเท่าที่ต้องการ (เพิ่มหลักของส่วนที่เป็นเศษส่วน) เนื่องจากมีตัวเลขในส่วนเสริมอื่น ๆ หรือ minuend

การคูณทศนิยมดำเนินการในลักษณะเดียวกับการคูณจำนวนธรรมชาติตามกฎเดียวกัน แต่ในผลคูณจะวางลูกน้ำตามผลรวมของตัวเลขของตัวประกอบในส่วนเศษส่วนโดยนับจากขวาไปซ้าย (ผลรวมของ หลักตัวคูณคือจำนวนหลักหลังจุดทศนิยมของตัวประกอบที่นำมารวมกัน)

ที่ การคูณทศนิยมในคอลัมน์แรกจากทางขวา ตัวเลขที่สำคัญลงนามใต้เลขนัยสำคัญตัวแรกทางด้านขวา เช่นเดียวกับเลขธรรมชาติ:

บันทึก การคูณทศนิยมในคอลัมน์:

บันทึก การหารทศนิยมในคอลัมน์:

อักขระที่ขีดเส้นใต้คืออักขระที่ตามด้วยลูกน้ำ เนื่องจากตัวหารต้องเป็นจำนวนเต็ม

กฎ. ที่ การหารเศษส่วนตัวหารทศนิยมจะเพิ่มขึ้นตามจำนวนหลักเท่าที่มีตัวเลขในส่วนที่เป็นเศษส่วน เพื่อให้แน่ใจว่าเศษส่วนไม่เปลี่ยนแปลง การจ่ายเงินปันผลจะเพิ่มขึ้นตามจำนวนหลักที่เท่ากัน (ในการจ่ายเงินปันผลและตัวหาร เครื่องหมายจุลภาคจะถูกย้ายไปยังจำนวนหลักเดียวกัน) ลูกน้ำจะถูกวางไว้ในผลหารที่ขั้นตอนการหารนั้นเมื่อใด ทั้งส่วนเศษส่วนจะถูกแบ่งออก

สำหรับเศษส่วนทศนิยม สำหรับจำนวนธรรมชาติ กฎยังคงอยู่: คุณไม่สามารถหารเศษส่วนทศนิยมด้วยศูนย์ได้!

ในบทเรียนที่แล้ว เราได้เรียนรู้วิธีการบวกและลบทศนิยม (ดูบท “การบวกและการลบทศนิยม”) ในเวลาเดียวกัน เราประเมินว่าการคำนวณจะง่ายขึ้นมากเพียงใดเมื่อเทียบกับเศษส่วน "สองชั้น" ทั่วไป

น่าเสียดายที่ผลกระทบนี้ไม่ได้เกิดขึ้นกับการคูณและหารทศนิยม ในบางกรณี สัญลักษณ์ทศนิยมอาจทำให้การดำเนินการเหล่านี้ซับซ้อนขึ้น

ก่อนอื่น เรามาแนะนำคำจำกัดความใหม่กันก่อน เราจะพบเขาค่อนข้างบ่อย ไม่ใช่แค่ในบทเรียนนี้เท่านั้น

ส่วนสำคัญของตัวเลขคือทุกอย่างระหว่างหลักแรกและหลักสุดท้ายที่ไม่ใช่ศูนย์ รวมถึงจุดสิ้นสุดด้วย เรากำลังพูดถึงตัวเลขเท่านั้น จุดทศนิยมจะไม่นำมาพิจารณา

ตัวเลขที่รวมอยู่ในส่วนสำคัญของตัวเลขเรียกว่าเลขนัยสำคัญ สามารถทำซ้ำได้และมีค่าเท่ากับศูนย์ด้วยซ้ำ

ตัวอย่างเช่น พิจารณาเศษส่วนทศนิยมหลายตัวแล้วเขียนส่วนสำคัญที่เกี่ยวข้อง:

1. 91.25 → 9125 (ตัวเลขสำคัญ: 9; 1; 2; 5);
2. 0.008241 → 8241 (ตัวเลขสำคัญ: 8; 2; 4; 1);
3. 15.0075 → 150075 (ตัวเลขสำคัญ: 1; 5; 0; 0; 7; 5);
4. 0.0304 → 304 (ตัวเลขสำคัญ: 3; 0; 4);
5. 3000 → 3 (มีเลขนัยสำคัญเพียงตัวเดียว: 3)

โปรดทราบ: เลขศูนย์ในส่วนสำคัญของตัวเลขจะไม่ไปไหนเลย เราได้พบสิ่งที่คล้ายกันแล้วเมื่อเราเรียนรู้ที่จะแปลงเศษส่วนทศนิยมเป็นเศษส่วนสามัญ (ดูบทเรียน “ ทศนิยม”)

ประเด็นนี้สำคัญมากและเกิดข้อผิดพลาดบ่อยมากจนฉันจะเผยแพร่การทดสอบในหัวข้อนี้ในอนาคตอันใกล้นี้ อย่าลืมฝึกฝน! และในความเป็นจริงแล้ว เราซึ่งมีแนวคิดเป็นส่วนสำคัญจึงจะดำเนินการตามหัวข้อของบทเรียนต่อไป

การคูณทศนิยม

การดำเนินการคูณประกอบด้วยสามขั้นตอนต่อเนื่องกัน:

1. สำหรับแต่ละเศษส่วน ให้เขียนส่วนสำคัญลงไป คุณจะได้จำนวนเต็มธรรมดาสองตัว - โดยไม่มีตัวส่วนและจุดทศนิยม
2. คูณตัวเลขเหล่านี้ด้วยค่าใดๆ ด้วยวิธีที่สะดวก- โดยตรงหากตัวเลขมีขนาดเล็กหรืออยู่ในคอลัมน์ เราได้ส่วนสำคัญของเศษส่วนที่ต้องการ
3. ค้นหาว่าจุดทศนิยมในเศษส่วนเดิมเลื่อนไปที่ไหนและกี่หลักเพื่อให้ได้ส่วนที่มีนัยสำคัญที่สอดคล้องกัน ดำเนินการกะย้อนกลับสำหรับส่วนสำคัญที่ได้รับในขั้นตอนก่อนหน้า

ฉันขอเตือนคุณอีกครั้งว่าศูนย์ที่ด้านข้างของส่วนสำคัญจะไม่ถูกนำมาพิจารณา การเพิกเฉยต่อกฎนี้ทำให้เกิดข้อผิดพลาด

1. 0.28 12.5;
2. 6.3 · 1.08;
3. 132.5 · 0.0034;
4. 0.0108 1600.5;
5. 5.25 · 10,000.

เราทำงานกับนิพจน์แรก: 0.28 · 12.5

1. มาเขียนส่วนสำคัญของตัวเลขจากนิพจน์นี้กัน: 28 และ 125;
2. สินค้า: 28 · 125 = 3500;
3. ในปัจจัยแรก จุดทศนิยมจะเลื่อนไปทางขวา 2 หลัก (0.28 → 28) และในวินาทีจะเลื่อนอีก 1 หลัก โดยรวมแล้วคุณต้องเลื่อนไปทางซ้ายสามหลัก: 3500 → 3,500 = 3.5

ทีนี้มาดูนิพจน์ 6.3 · 1.08 กัน

1. มาเขียนส่วนสำคัญกัน: 63 และ 108;
2. สินค้า: 63 · 108 = 6804;
3. อีกครั้ง เลื่อนไปทางขวาสองครั้ง: ทีละ 2 และ 1 หลัก ตามลำดับ รวม - อีกครั้ง 3 หลักทางด้านขวาดังนั้นการเปลี่ยนย้อนกลับจะเป็น 3 หลักทางซ้าย: 6804 → 6.804 คราวนี้ไม่มีศูนย์ต่อท้าย

เรามาถึงนิพจน์ที่สามแล้ว: 132.5 · 0.0034

1. ส่วนสำคัญ: 1325 และ 34;
2. สินค้า: 1325 · 34 = 45,050;
3. ในเศษส่วนแรกจุดทศนิยมจะเลื่อนไปทางขวา 1 หลักและในส่วนที่สอง - มากถึง 4 รวม: 5 ไปทางขวา เราเลื่อนไปทางซ้าย 5: 45,050 → .45050 = 0.4505 ศูนย์จะถูกลบออกในตอนท้าย และเพิ่มที่ด้านหน้าเพื่อไม่ให้มีจุดทศนิยม "เปลือย"

นิพจน์ต่อไปนี้คือ: 0.0108 · 1600.5

1. เราเขียนส่วนสำคัญ: 108 และ 16 005;
2. เราคูณมัน: 108 · 16,005 = 1,728,540;
3. เรานับตัวเลขหลังจุดทศนิยม: ในจำนวนแรกมี 4 ในจำนวนที่สองมี 1 รวมเป็น 5 อีกครั้ง เราได้: 1,728,540 → 17.28540 = 17.2854 ในตอนท้าย ศูนย์ "พิเศษ" ก็ถูกลบออก

สุดท้าย นิพจน์สุดท้าย: 5.25 10,000

1. ส่วนสำคัญ: 525 และ 1;
2. เราคูณพวกมัน: 525 · 1 = 525;
3. เศษส่วนแรกเลื่อนไปทางขวา 2 หลัก และเศษส่วนที่สองเลื่อนไปทางซ้าย 4 หลัก (10,000 → 1.0000 = 1) รวม 4 − 2 = 2 หลักทางซ้าย เราทำการย้อนกลับ 2 หลักทางด้านขวา: 525, → 52,500 (เราต้องเพิ่มศูนย์)

สังเกตตัวอย่างสุดท้าย: เนื่องจากจุดทศนิยมถูกย้ายไปที่ ทิศทางที่แตกต่างกันการเปลี่ยนแปลงทั้งหมดจะพบได้จากผลต่าง นี้เป็นอย่างมาก จุดสำคัญ- นี่เป็นอีกตัวอย่างหนึ่ง:

พิจารณาตัวเลข 1.5 และ 12,500 เรามี: 1.5 → 15 (เลื่อนไปทางขวา 1); 12,500 → 125 (เลื่อน 2 ไปทางซ้าย) เรา "ก้าว" ไปทางขวา 1 หลักแล้วไปทางซ้าย 2 หลัก เป็นผลให้เราก้าวไปทางซ้าย 2 − 1 = 1 หลัก

การหารทศนิยม

กองอาจจะมากที่สุด การดำเนินการที่ซับซ้อน- แน่นอน ที่นี่คุณสามารถดำเนินการโดยการเปรียบเทียบกับการคูณ: หารส่วนสำคัญแล้ว "ย้าย" จุดทศนิยม แต่ในกรณีนี้ มีรายละเอียดปลีกย่อยมากมายเกิดขึ้นซึ่งทำให้ไม่สามารถประหยัดได้

ดังนั้นเรามาดูอัลกอริธึมสากลซึ่งยาวกว่าเล็กน้อย แต่มีความน่าเชื่อถือมากกว่า:

1. แปลงเศษส่วนทศนิยมทั้งหมดให้เป็นเศษส่วนสามัญ เพียงฝึกฝนเพียงเล็กน้อย ขั้นตอนนี้จะใช้เวลาไม่กี่วินาที
2. แบ่งเศษส่วนผลลัพธ์ด้วยวิธีคลาสสิก กล่าวอีกนัยหนึ่งให้คูณเศษส่วนแรกด้วยวินาทีที่ "กลับด้าน" (ดูบทเรียน "การคูณและหารเศษส่วนตัวเลข");
3. ถ้าเป็นไปได้ ให้นำเสนอผลลัพธ์อีกครั้งเป็นเศษส่วนทศนิยม ขั้นตอนนี้ต้องทำอย่างรวดเร็วเช่นกัน เนื่องจากตัวส่วนมักจะมีกำลังเป็นสิบอยู่แล้ว

งาน. ค้นหาความหมายของสำนวน:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

ลองพิจารณาการแสดงออกแรก ขั้นแรก เรามาแปลงเศษส่วนเป็นทศนิยมกันก่อน:

ลองทำแบบเดียวกันกับนิพจน์ที่สองกัน ตัวเศษของเศษส่วนแรกจะถูกแยกตัวประกอบอีกครั้ง:

มีจุดสำคัญในตัวอย่างที่สามและสี่: หลังจากกำจัดเครื่องหมายทศนิยมแล้ว เศษส่วนที่ลดได้ จะปรากฏขึ้น อย่างไรก็ตาม เราจะไม่ดำเนินการลดหย่อนนี้

ตัวอย่างสุดท้ายน่าสนใจเพราะตัวเศษของเศษส่วนหลังมีจำนวนเฉพาะ ไม่มีอะไรต้องแยกตัวประกอบที่นี่ ดังนั้นเราจึงพิจารณาตรงไปตรงมา:

บางครั้งการหารจะให้ผลลัพธ์เป็นจำนวนเต็ม (ฉันกำลังพูดถึงตัวอย่างสุดท้าย) ในกรณีนี้ ขั้นตอนที่สามจะไม่ดำเนินการเลย

นอกจากนี้ เมื่อทำการหาร เศษส่วนที่ “น่าเกลียด” มักจะเกิดขึ้นซึ่งไม่สามารถแปลงเป็นทศนิยมได้ สิ่งนี้ทำให้การหารแตกต่างจากการคูณ โดยที่ผลลัพธ์จะแสดงในรูปแบบทศนิยมเสมอ แน่นอน ในกรณีนี้ ขั้นตอนสุดท้ายจะไม่ดำเนินการอีกครั้ง

ให้ความสนใจกับตัวอย่างที่ 3 และ 4 ด้วย ในนั้นเราไม่ได้จงใจย่อให้สั้นลง เศษส่วนสามัญมาจากทศนิยม มิฉะนั้น จะทำให้งานผกผันซับซ้อนขึ้น โดยแสดงคำตอบสุดท้ายอีกครั้งในรูปแบบทศนิยม

ข้อควรจำ: คุณสมบัติพื้นฐานของเศษส่วน (เช่นเดียวกับกฎอื่นๆ ในคณิตศาสตร์) ในตัวมันเองไม่ได้หมายความว่าจะต้องนำไปใช้ทุกที่และทุกเวลา ในทุกโอกาส

เช่นเดียวกับตัวเลขปกติ

2. เรานับจำนวนตำแหน่งทศนิยมของเศษส่วนทศนิยมตัวที่ 1 และตัวที่ 2 เราบวกตัวเลขของพวกเขา

3. ผลลัพธ์สุดท้ายให้นับจากขวาไปซ้ายตามจำนวนหลักตามย่อหน้าข้างต้นแล้วใส่ลูกน้ำ

กฎสำหรับการคูณเศษส่วนทศนิยม

1. คูณโดยไม่ต้องสนใจเครื่องหมายจุลภาค

2. ในผลคูณเราแยกจำนวนหลักหลังจุดทศนิยมให้เท่ากันกับจำนวนหลักหลังจุดทศนิยมทั้งสองตัวรวมกัน

เมื่อคูณเศษส่วนทศนิยมด้วยจำนวนธรรมชาติ คุณต้อง:

1. คูณตัวเลขโดยไม่ต้องสนใจเครื่องหมายจุลภาค

2. ด้วยเหตุนี้ เราจึงวางลูกน้ำเพื่อให้มีหลักทางด้านขวาเท่ากับจำนวนที่เป็นเศษส่วนทศนิยม

การคูณเศษส่วนทศนิยมตามคอลัมน์

ลองดูตัวอย่าง:

เราเขียนเศษส่วนทศนิยมลงในคอลัมน์แล้วคูณเป็นตัวเลขธรรมชาติโดยไม่ต้องสนใจเครื่องหมายจุลภาค เหล่านั้น. เราถือว่า 3.11 เป็น 311 และ 0.01 เป็น 1

ผลลัพธ์คือ 311 ต่อไป เราจะนับจำนวนเครื่องหมาย (หลัก) หลังจุดทศนิยมของเศษส่วนทั้งสอง ทศนิยมตัวแรกมี 2 หลัก และตัวที่ 2 มี 2 จำนวนทั้งหมดตัวเลขหลังจุดทศนิยม:

2 + 2 = 4

เรานับผลลัพธ์สี่หลักจากขวาไปซ้าย ผลลัพธ์สุดท้ายมีตัวเลขน้อยกว่าที่ต้องคั่นด้วยลูกน้ำ ในกรณีนี้ คุณต้องเพิ่มจำนวนศูนย์ที่หายไปทางด้านซ้าย

ในกรณีของเรา ตัวเลขตัวแรกหายไป ดังนั้นเราจึงบวก 1 ไปทางซ้าย

บันทึก:

เมื่อคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 เป็นต้น จุดทศนิยมในเศษส่วนทศนิยมจะถูกย้ายไปทางขวาตามจำนวนตำแหน่งที่มีศูนย์อยู่หลังตำแหน่งหนึ่ง

ตัวอย่างเช่น:

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

บันทึก:

หากต้องการคูณทศนิยมด้วย 0.1; 0.01; 0.001; และต่อจากนี้ คุณจะต้องย้ายจุดทศนิยมในเศษส่วนนี้ไปทางซ้ายให้มากที่สุดเท่าที่มีศูนย์อยู่ข้างหน้าจุดนั้น

เรานับแม้กระทั่งศูนย์!

ตัวอย่างเช่น:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

ในบทช่วยสอนนี้ เราจะดูการดำเนินการแต่ละรายการแยกกัน

เนื้อหาบทเรียน

การบวกทศนิยม

ดังที่เราทราบ เศษส่วนทศนิยมมีทั้งจำนวนเต็มและเศษส่วน เมื่อบวกทศนิยม ส่วนทั้งหมดและเศษส่วนจะถูกบวกแยกกัน

ตัวอย่างเช่น ลองบวกเศษส่วนทศนิยม 3.2 และ 5.3 การบวกเศษส่วนทศนิยมในคอลัมน์จะสะดวกกว่า

ขั้นแรกให้เราเขียนเศษส่วนทั้งสองนี้ลงในคอลัมน์ โดยส่วนที่เป็นจำนวนเต็มจะต้องอยู่ใต้จำนวนเต็ม และส่วนที่เป็นเศษส่วนอยู่ใต้เศษส่วน ที่โรงเรียนเรียกว่าข้อกำหนดนี้ "ลูกน้ำใต้ลูกน้ำ".

ลองเขียนเศษส่วนลงในคอลัมน์โดยให้ลูกน้ำอยู่ใต้ลูกน้ำ:

เราเริ่มบวกเศษส่วน: 2 + 3 = 5 เราเขียนห้าในส่วนที่เป็นเศษส่วนของคำตอบ:

ตอนนี้เรารวมส่วนทั้งหมดเข้าด้วยกัน: 3 + 5 = 8 เราเขียนแปดในส่วนทั้งหมดของคำตอบ:

ตอนนี้เราแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้เราปฏิบัติตามกฎอีกครั้ง "ลูกน้ำใต้ลูกน้ำ":

เราได้รับคำตอบ 8.5 ดังนั้นนิพจน์ 3.2 + 5.3 เท่ากับ 8.5

ที่จริงแล้วไม่ใช่ทุกอย่างจะง่ายอย่างที่คิดเมื่อเห็นแวบแรก นอกจากนี้ยังมีข้อผิดพลาดที่นี่ซึ่งเราจะพูดถึงตอนนี้

ตำแหน่งเป็นทศนิยม

เศษส่วนทศนิยมก็เหมือนกับตัวเลขทั่วไปที่มีตัวเลขเป็นของตัวเอง เหล่านี้เป็นสถานที่ที่สิบ, ที่ร้อย, ที่หนึ่งในพัน. ในกรณีนี้ ตัวเลขจะเริ่มต้นหลังจุดทศนิยม

หลักแรกหลังจุดทศนิยมมีหน้าที่รับผิดชอบในตำแหน่งที่สิบ หลักที่สองหลังจุดทศนิยมคือหลักร้อย และหลักที่สามหลังจุดทศนิยมคือหลักพัน

ตำแหน่งที่เป็นเศษส่วนทศนิยมก็มีอยู่บ้าง ข้อมูลที่เป็นประโยชน์- โดยเฉพาะอย่างยิ่ง พวกเขาบอกคุณว่ามีทศนิยมกี่ในสิบ ร้อย และหนึ่งในพัน

เช่น พิจารณาเศษส่วนทศนิยม 0.345

ตำแหน่งที่ทั้งสามตั้งอยู่เรียกว่า อันดับที่สิบ

ตำแหน่งที่ทั้งสี่ตั้งอยู่เรียกว่า อันดับที่ร้อย

ตำแหน่งที่ทั้งห้าตั้งอยู่เรียกว่า อันดับที่พัน

ลองดูภาพวาดนี้ เราเห็นว่ามีสามอยู่ในตำแหน่งที่สิบ. สิ่งนี้บอกเราว่ามีสามในสิบของเศษส่วนทศนิยม 0.345

ถ้าเราบวกเศษส่วน เราจะได้เศษส่วนทศนิยมเดิม 0.345

จะเห็นได้ว่าตอนแรกเราได้คำตอบแต่เราแปลงเป็นเศษส่วนทศนิยมแล้วได้ 0.345

เมื่อบวกเศษส่วนทศนิยม จะต้องปฏิบัติตามหลักการและกฎเดียวกันกับเมื่อบวกเลขธรรมดา การบวกเศษส่วนทศนิยมเกิดขึ้นในหลัก: ส่วนที่สิบจะถูกบวกเข้ากับหลักสิบ, หลักร้อยถึงหลักร้อย, หลักพันถึงหลักพัน

ดังนั้นการบวกเศษส่วนทศนิยมต้องเป็นไปตามกฎ "ลูกน้ำใต้ลูกน้ำ"- เครื่องหมายจุลภาคใต้เครื่องหมายจุลภาคระบุลำดับของการบวกหนึ่งในสิบเข้ากับสิบ, ในร้อยถึงหลักร้อย, ในพันถึงในพัน

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 1.5 + 3.4

ก่อนอื่น เราบวกเศษส่วน 5 + 4 = 9 เราเขียนเก้าในส่วนที่เป็นเศษส่วนของคำตอบ:

ตอนนี้เราบวกจำนวนเต็มส่วนที่ 1 + 3 = 4 เราเขียนสี่ในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการดำเนินการนี้ ให้ปฏิบัติตามกฎ "ลูกน้ำใต้ลูกน้ำ" อีกครั้ง:

เราได้รับคำตอบ 4.9 ซึ่งหมายความว่าค่าของนิพจน์ 1.5 + 3.4 คือ 4.9

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์: 3.51 + 1.22

เราเขียนนิพจน์นี้ในคอลัมน์โดยสังเกตกฎ "ลูกน้ำใต้ลูกน้ำ"

ก่อนอื่น เราบวกเศษส่วนเข้าด้วยกัน ซึ่งก็คือส่วนในร้อยของ 1+2=3 เราเขียนคำตอบสามเท่าในส่วนที่ร้อย:

ตอนนี้บวกส่วนที่สิบ 5+2=7 เราเขียนเจ็ดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เราบวกทั้งส่วน 3+1=4 เราเขียนทั้งสี่ในส่วนทั้งหมดของคำตอบของเรา:

เราแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ โดยปฏิบัติตามกฎ "ลูกน้ำใต้ลูกน้ำ":

คำตอบที่เราได้รับคือ 4.73 ซึ่งหมายความว่าค่าของนิพจน์ 3.51 + 1.22 เท่ากับ 4.73

3,51 + 1,22 = 4,73

เช่นเดียวกับตัวเลขทั่วไป เมื่อบวกทศนิยม . ในกรณีนี้คำตอบจะเขียนหนึ่งหลักและส่วนที่เหลือจะถูกโอนไปยังหลักถัดไป

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 2.65 + 3.27

เราเขียนนิพจน์นี้ลงในคอลัมน์:

เพิ่มส่วนที่ร้อย 5+7=12 หมายเลข 12 จะไม่พอดีกับส่วนที่ร้อยของคำตอบของเรา ดังนั้นในส่วนที่ร้อยเราจึงเขียนเลข 2 และย้ายหน่วยไปที่หลักถัดไป:

ตอนนี้เราบวกหนึ่งในสิบของ 6 + 2 = 8 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 9 เราเขียนเลข 9 ในส่วนที่สิบของคำตอบ:

ตอนนี้เราบวกทั้งส่วน 2+3=5 เราเขียนเลข 5 ไว้ในส่วนจำนวนเต็มของคำตอบ:

เราได้รับคำตอบ 5.92 ซึ่งหมายความว่าค่าของนิพจน์ 2.65 + 3.27 เท่ากับ 5.92

2,65 + 3,27 = 5,92

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ 9.5 + 2.8

เราเขียนนิพจน์นี้ลงในคอลัมน์

เราบวกเศษส่วน 5 + 8 = 13 ตัวเลข 13 จะไม่พอดีกับเศษส่วนของคำตอบ ดังนั้นเราจึงเขียนเลข 3 ก่อนแล้วย้ายหน่วยไปที่หลักถัดไป หรือโอนไปที่ ส่วนจำนวนเต็ม:

ตอนนี้เราบวกส่วนจำนวนเต็ม 9+2=11 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 12 เราเขียนเลข 12 ไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 12.3. ซึ่งหมายความว่าค่าของนิพจน์ 9.5 + 2.8 คือ 12.3

9,5 + 2,8 = 12,3

เมื่อบวกทศนิยม จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองจะต้องเท่ากัน หากมีตัวเลขไม่เพียงพอ สถานที่เหล่านี้ในส่วนเศษส่วนจะเต็มไปด้วยศูนย์

ตัวอย่างที่ 5- ค้นหาค่าของนิพจน์: 12.725 + 1.7

ก่อนที่จะเขียนนิพจน์นี้ในคอลัมน์ เรามาทำให้จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองเท่ากันก่อน เศษส่วนทศนิยม 12.725 มีเลขสามหลักหลังจุดทศนิยม แต่เศษส่วน 1.7 มีเพียงเลขเดียว ซึ่งหมายความว่าในส่วน 1.7 คุณต้องเพิ่มศูนย์สองตัวต่อท้าย แล้วเราจะได้เศษส่วน 1.700. ตอนนี้คุณสามารถเขียนนิพจน์นี้ลงในคอลัมน์และเริ่มคำนวณได้:

บวกหนึ่งในพันส่วน 5+0=5 เราเขียนเลข 5 ในส่วนหนึ่งในพันของคำตอบ:

เพิ่มส่วนที่ร้อย 2+0=2 เราเขียนหมายเลข 2 ในส่วนที่ร้อยของคำตอบ:

บวกส่วนสิบ 7+7=14 หมายเลข 14 จะไม่พอดีกับหนึ่งในสิบของคำตอบของเรา ดังนั้นเราจึงเขียนเลข 4 ก่อนแล้วเลื่อนหน่วยไปที่หลักถัดไป:

ตอนนี้เราบวกส่วนจำนวนเต็ม 12+1=13 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 14 เราเขียนเลข 14 ไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 14,425 คน ซึ่งหมายความว่าค่าของนิพจน์ 12.725+1.700 คือ 14.425

12,725+ 1,700 = 14,425

การลบทศนิยม

เมื่อลบเศษส่วนทศนิยมคุณต้องปฏิบัติตามกฎเดียวกันกับการบวก: “ลูกน้ำใต้ลูกน้ำ” และ “ ปริมาณเท่ากันตัวเลขหลังจุดทศนิยม”

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 2.5 − 2.2

เราเขียนนิพจน์นี้ในคอลัมน์โดยสังเกตกฎ "ลูกน้ำใต้ลูกน้ำ":

เราคำนวณเศษส่วน 5−2=3 เราเขียนหมายเลข 3 ในส่วนที่สิบของคำตอบ:

เราคำนวณจำนวนเต็มส่วนที่ 2−2=0 เราเขียนศูนย์ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 0.3 ซึ่งหมายความว่าค่าของนิพจน์ 2.5 - 2.2 เท่ากับ 0.3

2,5 − 2,2 = 0,3

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 7.353 - 3.1

นิพจน์นี้มีทศนิยมจำนวนต่างกัน เศษส่วน 7.353 มีเลขสามหลักหลังจุดทศนิยม แต่เศษส่วน 3.1 มีเพียงเลขเดียว ซึ่งหมายความว่าในเศษส่วน 3.1 คุณต้องเพิ่มศูนย์สองตัวต่อท้ายเพื่อทำให้จำนวนหลักในเศษส่วนทั้งสองเท่ากัน แล้วเราจะได้ 3,100.

ตอนนี้คุณสามารถเขียนนิพจน์นี้ลงในคอลัมน์แล้วคำนวณได้:

เราได้รับคำตอบ 4,253 คน ซึ่งหมายความว่าค่าของนิพจน์ 7.353 − 3.1 เท่ากับ 4.253

7,353 — 3,1 = 4,253

เช่นเดียวกับตัวเลขธรรมดา บางครั้งคุณจะต้องยืมเลขหนึ่งจากเลขหลักที่อยู่ติดกันหากการลบเป็นไปไม่ได้

ตัวอย่างที่ 3จงหาค่าของนิพจน์ 3.46 − 2.39

ลบหนึ่งในร้อยของ 6−9 คุณไม่สามารถลบเลข 9 จากเลข 6 ได้ ดังนั้นคุณต้องยืมเลขหนึ่งจากเลขหลักที่อยู่ติดกัน โดยการยืมหนึ่งจากหลักที่อยู่ติดกัน เลข 6 จะกลายเป็นเลข 16 ตอนนี้คุณสามารถคำนวณหนึ่งในร้อยของ 16−9=7 ได้ เราเขียนคำตอบเจ็ดส่วนในร้อย:

ตอนนี้เราลบสิบ. เนื่องจากเราได้หนึ่งหน่วยในอันดับที่สิบ จำนวนตัวเลขที่อยู่ตรงนั้นจึงลดลงหนึ่งหน่วย กล่าวอีกนัยหนึ่ง ในอันดับที่สิบตอนนี้ไม่ใช่เลข 4 แต่เป็นเลข 3 ลองคำนวณหนึ่งในสิบของ 3−3=0 กัน เราเขียนศูนย์ในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เราลบส่วนทั้งหมด 3−2=1 เราเขียนไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 1.07 ซึ่งหมายความว่าค่าของนิพจน์ 3.46−2.39 เท่ากับ 1.07

3,46−2,39=1,07

ตัวอย่างที่ 4- ค้นหาค่าของนิพจน์ 3−1.2

ตัวอย่างนี้จะลบทศนิยมจากจำนวนเต็ม ลองเขียนนิพจน์นี้ลงในคอลัมน์เพื่อให้เศษส่วนทศนิยม 1.23 ทั้งหมดอยู่ใต้เลข 3

ทีนี้ลองทำให้จำนวนหลักหลังจุดทศนิยมเท่ากัน ในการทำเช่นนี้หลังจากหมายเลข 3 เราใส่เครื่องหมายจุลภาคและเพิ่มศูนย์หนึ่งตัว:

ตอนนี้เราลบสิบ: 0−2 คุณไม่สามารถลบเลข 2 จากศูนย์ได้ ดังนั้น คุณต้องยืมเลขตัวหนึ่งจากหลักที่อยู่ติดกัน เมื่อยืมมาหนึ่งตัวจากหลักข้างเคียง 0 จะเปลี่ยนเป็นเลข 10 ตอนนี้คุณสามารถคำนวณหนึ่งในสิบของ 10−2=8 ได้ เราเขียนแปดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เราลบส่วนทั้งหมดออก ก่อนหน้านี้หมายเลข 3 ตั้งอยู่ทั้งหมด แต่เราเอามาหนึ่งหน่วยจากมัน เป็นผลให้มันกลายเป็นเลข 2 ดังนั้นจาก 2 เราลบ 1 2−1=1 เราเขียนไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

คำตอบที่เราได้รับคือ 1.8 ซึ่งหมายความว่าค่าของนิพจน์ 3−1.2 คือ 1.8

การคูณทศนิยม

การคูณทศนิยมนั้นง่ายและสนุกด้วยซ้ำ หากต้องการคูณทศนิยม คุณต้องคูณมันเหมือนตัวเลขปกติ โดยไม่สนใจเครื่องหมายจุลภาค

เมื่อได้รับคำตอบแล้ว คุณจะต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสอง จากนั้นนับจำนวนหลักเท่ากันจากทางขวาในคำตอบแล้วใส่ลูกน้ำ

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 2.5 × 1.5

ลองคูณเศษส่วนทศนิยมเหมือนตัวเลขธรรมดา โดยไม่สนใจลูกน้ำ หากต้องการเพิกเฉยต่อเครื่องหมายจุลภาค คุณสามารถจินตนาการได้ว่าเครื่องหมายเหล่านั้นหายไปเลย:

เราได้ 375 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.5 และ 1.5 เศษส่วนแรกมีหนึ่งหลักหลังจุดทศนิยม และเศษส่วนที่สองก็มีหนึ่งหลักด้วย รวมสองตัวเลข

เรากลับไปที่หมายเลข 375 และเริ่มเคลื่อนจากขวาไปซ้าย เราจำเป็นต้องนับตัวเลขสองหลักทางด้านขวาและใส่ลูกน้ำ:

เราได้คำตอบ 3.75 ดังนั้นค่าของนิพจน์ 2.5 × 1.5 คือ 3.75

2.5 × 1.5 = 3.75

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 12.85 × 2.7

ลองคูณเศษส่วนทศนิยมเหล่านี้โดยไม่สนใจลูกน้ำ:

เราได้รับ 34695 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 12.85 และ 2.7 เศษส่วน 12.85 มีตัวเลขสองหลักหลังจุดทศนิยม และเศษส่วน 2.7 มีตัวเลขหนึ่งหลัก - รวมเป็นสามหลัก

เรากลับไปที่หมายเลข 34695 และเริ่มย้ายจากขวาไปซ้าย เราต้องนับสามหลักจากทางขวาและใส่ลูกน้ำ:

เราได้รับคำตอบ 34,695 คน ดังนั้นค่าของนิพจน์ 12.85 × 2.7 คือ 34.695

12.85 × 2.7 = 34.695

การคูณทศนิยมด้วยจำนวนปกติ

บางครั้งสถานการณ์เกิดขึ้นเมื่อคุณต้องการคูณเศษส่วนทศนิยมด้วยจำนวนปกติ

หากต้องการคูณทศนิยมและตัวเลข คุณต้องคูณพวกมันโดยไม่ต้องสนใจเครื่องหมายจุลภาคในทศนิยม เมื่อได้รับคำตอบแล้ว คุณจะต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทศนิยมจากนั้นนับจำนวนหลักเท่ากันจากทางขวาในคำตอบแล้วใส่ลูกน้ำ

เช่น คูณ 2.54 ด้วย 2

คูณเศษส่วนทศนิยม 2.54 ด้วยตัวเลขปกติ 2 โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้หมายเลข 508 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.54 เศษส่วน 2.54 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 508 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับตัวเลขสองหลักทางด้านขวาและใส่ลูกน้ำ:

เราได้รับคำตอบ 5.08 ดังนั้นค่าของนิพจน์ 2.54 × 2 คือ 5.08

2.54 × 2 = 5.08

การคูณทศนิยมด้วย 10, 100, 1,000

การคูณทศนิยมด้วย 10, 100 หรือ 1,000 จะทำในลักษณะเดียวกับการคูณทศนิยมด้วยตัวเลขปกติ คุณต้องทำการคูณโดยไม่สนใจลูกน้ำในเศษส่วนทศนิยมจากนั้นในคำตอบให้แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนโดยนับจากทางขวาด้วยจำนวนหลักเท่ากันเนื่องจากมีตัวเลขอยู่หลังจุดทศนิยม

เช่น คูณ 2.88 ด้วย 10

คูณเศษส่วนทศนิยม 2.88 ด้วย 10 โดยไม่สนใจเครื่องหมายจุลภาคในเศษส่วนทศนิยม:

เราได้ 2880 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.88 เราจะเห็นว่าเศษส่วน 2.88 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 2880 และเริ่มย้ายจากขวาไปซ้าย เราต้องนับตัวเลขสองหลักทางด้านขวาและใส่ลูกน้ำ:

เราได้รับคำตอบ 28.80. ลองปล่อยศูนย์สุดท้ายแล้วได้ 28.8 ซึ่งหมายความว่าค่าของนิพจน์ 2.88×10 คือ 28.8

2.88 × 10 = 28.8

มีวิธีที่สองในการคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยการเลื่อนจุดทศนิยมไปทางขวาตามหลักจำนวนเท่าที่มีเลขศูนย์อยู่ในตัวประกอบ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 2.88×10 ด้วยวิธีนี้ เราจะดูปัจจัย 10 ทันทีโดยไม่ต้องคำนวณใดๆ เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามีศูนย์หนึ่งตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลัก เราได้ 28.8

2.88 × 10 = 28.8

ลองคูณ 2.88 ด้วย 100 ดูตัวประกอบ 100 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามีศูนย์สองตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาสองหลัก จะได้ 288

2.88 × 100 = 288

ลองคูณ 2.88 ด้วย 1,000 ดูตัวประกอบ 1,000 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามีศูนย์สามตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาสามหลัก ไม่มีหลักที่สามดังนั้นเราจึงบวกศูนย์อีกตัวหนึ่ง เป็นผลให้เราได้ 2880

2.88 × 1,000 = 2880

การคูณทศนิยมด้วย 0.1 0.01 และ 0.001

การคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 มีการทำงานในลักษณะเดียวกับการคูณทศนิยมด้วยทศนิยม จำเป็นต้องคูณเศษส่วนเหมือนตัวเลขธรรมดาแล้วใส่ลูกน้ำในคำตอบโดยนับหลักทางด้านขวาเท่ากับจำนวนหลักที่อยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

เช่น คูณ 3.25 ด้วย 0.1

เราคูณเศษส่วนเหล่านี้เหมือนตัวเลขธรรมดา โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 325 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 3.25 และ 0.1 เศษส่วน 3.25 มีตัวเลขสองหลักหลังจุดทศนิยม และเศษส่วน 0.1 มีตัวเลขหนึ่งหลัก รวมสามตัวเลข

เรากลับไปที่หมายเลข 325 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับสามหลักจากทางขวาและใส่ลูกน้ำ หลังจากนับถอยหลังสามหลักก็พบว่าตัวเลขหมด ในกรณีนี้ คุณต้องเพิ่มศูนย์หนึ่งตัวและใส่ลูกน้ำ:

เราได้รับคำตอบ 0.325 ซึ่งหมายความว่าค่าของนิพจน์ 3.25 × 0.1 คือ 0.325

3.25 × 0.1 = 0.325

มีวิธีที่สองในการคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยการเลื่อนจุดทศนิยมไปทางซ้ายตามหลักจำนวนเท่าที่มีเลขศูนย์อยู่ในตัวประกอบ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 3.25 × 0.1 ด้วยวิธีนี้ โดยไม่ต้องคำนวณใดๆ เราจะดูตัวคูณ 0.1 ทันที เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์หนึ่งตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 3.25 เราเลื่อนจุดทศนิยมไปทางซ้ายหนึ่งหลัก โดยการเลื่อนเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลัก เราจะเห็นว่าไม่มีหลักอื่นอยู่ก่อนหลักสามหลัก ในกรณีนี้ ให้เพิ่มศูนย์หนึ่งตัวและใส่ลูกน้ำ ผลลัพธ์คือ 0.325

3.25 × 0.1 = 0.325

ลองคูณ 3.25 ด้วย 0.01 กัน เราจะดูตัวคูณ 0.01 ทันที เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์สองตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 3.25 เราย้ายจุดทศนิยมไปทางซ้ายสองหลัก เราได้ 0.0325

3.25 × 0.01 = 0.0325

ลองคูณ 3.25 ด้วย 0.001 กัน เราจะดูตัวคูณ 0.001 ทันที เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์สามตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 3.25 เราย้ายจุดทศนิยมไปทางซ้ายสามหลัก เราได้ 0.00325

3.25 × 0.001 = 0.00325

อย่าสับสนกับการคูณเศษส่วนทศนิยมด้วย 0.1, 0.001 และ 0.001 ด้วยการคูณ 10, 100, 1,000 ข้อผิดพลาดทั่วไปคนส่วนใหญ่

เมื่อคูณด้วย 10, 100, 1,000 จุดทศนิยมจะเลื่อนไปทางขวาด้วยจำนวนหลักเท่ากันเนื่องจากมีเลขศูนย์อยู่ในตัวคูณ

และเมื่อคูณด้วย 0.1, 0.01 และ 0.001 จุดทศนิยมจะเลื่อนไปทางซ้ายด้วยจำนวนหลักเท่ากันเนื่องจากมีเลขศูนย์อยู่ในตัวคูณ

หากจำยากในตอนแรก คุณสามารถใช้วิธีแรก ซึ่งจะทำการคูณเช่นเดียวกับตัวเลขธรรมดา ในคำตอบคุณจะต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนโดยนับเลขหลักทางด้านขวาเนื่องจากมีตัวเลขหลังจุดทศนิยมในเศษส่วนทั้งสอง

การหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า ระดับสูง.

ในบทเรียนก่อนหน้านี้บทหนึ่ง เราบอกว่าเมื่อหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า จะได้เศษส่วนมา โดยตัวเศษคือเงินปันผล และตัวส่วนคือตัวหาร

ตัวอย่างเช่น หากต้องการแบ่งแอปเปิ้ลหนึ่งผลระหว่างสอง คุณต้องเขียน 1 (แอปเปิ้ลหนึ่งผล) ในตัวเศษ และเขียน 2 (เพื่อนสองคน) ในตัวส่วน ผลลัพธ์ที่ได้คือเศษส่วน ซึ่งหมายความว่าเพื่อนแต่ละคนจะได้รับแอปเปิ้ล กล่าวอีกนัยหนึ่งคือแอปเปิ้ลครึ่งลูก เศษส่วนคือคำตอบของปัญหา “วิธีแบ่งแอปเปิ้ลหนึ่งผลออกเป็นสองผล”

ปรากฎว่าคุณสามารถแก้ปัญหานี้ต่อไปได้หากคุณหาร 1 ด้วย 2 ท้ายที่สุดแล้ว เส้นเศษส่วนในเศษส่วนใดๆ ก็หมายถึงการหาร ดังนั้น การหารนี้จึงได้รับอนุญาตให้เป็นเศษส่วนได้ แต่อย่างไร? เราคุ้นเคยกับความจริงที่ว่าเงินปันผลจะมากกว่าตัวหารเสมอ แต่ตรงนี้ ตรงกันข้าม เงินปันผลน้อยกว่าตัวหาร.

ทุกอย่างจะชัดเจนถ้าเราจำไว้ว่าเศษส่วนหมายถึงการแตกสลาย การแบ่ง การแบ่ง ซึ่งหมายความว่าหน่วยสามารถแบ่งออกเป็นส่วนต่างๆ ได้มากเท่าที่ต้องการ ไม่ใช่แค่เพียงสองส่วนเท่านั้น

เมื่อคุณหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากขึ้น คุณจะได้เศษส่วนทศนิยมซึ่งส่วนของจำนวนเต็มคือ 0 (ศูนย์) เศษส่วนสามารถเป็นอะไรก็ได้

ลองหาร 1 ด้วย 2 กัน ลองแก้ตัวอย่างนี้ด้วยมุม:

หนึ่งไม่สามารถแบ่งออกเป็นสองอย่างสมบูรณ์ หากคุณถามคำถาม “หนึ่งมีกี่สอง” แล้วคำตอบจะเป็น 0 ดังนั้นในผลหารเราจึงเขียน 0 และใส่ลูกน้ำ:

ตามปกติแล้ว เราคูณผลหารด้วยตัวหารเพื่อให้ได้ส่วนที่เหลือ:

ถึงเวลาแล้วที่หน่วยสามารถแบ่งออกเป็นสองส่วนได้ เมื่อต้องการทำเช่นนี้ ให้เพิ่มศูนย์อีกตัวทางด้านขวาของผลลัพธ์:

เราได้ 10. หาร 10 ด้วย 2 เราได้ 5. เราเขียนห้าไว้ในส่วนของเศษส่วนของคำตอบ:

ตอนนี้เรานำส่วนที่เหลือสุดท้ายออกมาเพื่อคำนวณให้เสร็จสิ้น คูณ 5 ด้วย 2 เพื่อให้ได้ 10

เราได้รับคำตอบ 0.5 ดังนั้นเศษส่วนคือ 0.5

แอปเปิลครึ่งลูกสามารถเขียนได้โดยใช้เศษส่วนทศนิยม 0.5 หากเราเพิ่มทั้งสองซีกนี้ (0.5 และ 0.5) เราจะได้แอปเปิ้ลดั้งเดิมทั้งหมดอีกครั้ง:

ประเด็นนี้สามารถเข้าใจได้หากคุณจินตนาการว่า 1 ซม. แบ่งออกเป็นสองส่วนอย่างไร ถ้าแบ่ง 1 เซนติเมตรออกเป็น 2 ส่วน จะได้ 0.5 ซม

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 4:5

มีห้ากี่ในสี่? ไม่เลย. เราเขียน 0 ลงในผลหารและใส่ลูกน้ำ:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียนศูนย์ไว้ใต้เลขสี่. ลบศูนย์นี้ออกจากเงินปันผลทันที:

ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) สี่ส่วนออกเป็น 5 ส่วนกัน เมื่อต้องการทำสิ่งนี้ ให้บวกศูนย์ทางด้านขวาของ 4 แล้วหาร 40 ด้วย 5 เราจะได้ 8 เราเขียน 8 ลงในผลหาร

เราทำตัวอย่างให้สมบูรณ์โดยการคูณ 8 ด้วย 5 เพื่อให้ได้ 40:

เราได้รับคำตอบ 0.8 ซึ่งหมายความว่าค่าของนิพจน์ 4:5 คือ 0.8

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 5: 125

125 มีกี่หมายเลขในห้า? ไม่เลย. เราเขียน 0 ลงในผลหารและใส่ลูกน้ำ:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียน 0 ใต้ห้า. ลบ 0 จากห้าทันที

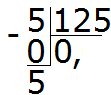
ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) ห้าส่วนออกเป็น 125 ส่วนกัน เมื่อต้องการทำสิ่งนี้ ให้เขียนศูนย์ทางด้านขวาของห้าค่านี้:

หาร 50 ด้วย 125 จำนวน 125 ในจำนวน 50 มีกี่หมายเลข? ไม่เลย. ในผลหารเราจึงเขียน 0 อีกครั้ง

คูณ 0 ด้วย 125 เราจะได้ 0 เขียนศูนย์นี้ไว้ใต้ 50 ลบ 0 ออกจาก 50 ทันที

ตอนนี้แบ่งจำนวน 50 ออกเป็น 125 ส่วน เมื่อต้องการทำสิ่งนี้ ให้เขียนศูนย์อีกอันทางด้านขวาของ 50:

หาร 500 ด้วย 125 จำนวน 125 ในจำนวน 500 มีกี่จำนวน 125 มีสี่จำนวนในจำนวน 500 เขียนสี่ลงในผลหาร:

เราทำตัวอย่างให้สมบูรณ์โดยคูณ 4 ด้วย 125 เพื่อให้ได้ 500

เราได้รับคำตอบ 0.04 ซึ่งหมายความว่าค่าของนิพจน์ 5: 125 คือ 0.04

การหารตัวเลขโดยไม่มีเศษ

ดังนั้น ให้ใส่ลูกน้ำหลังหน่วยในผลหาร เพื่อเป็นการระบุว่าการหารส่วนจำนวนเต็มสิ้นสุดลงแล้ว และเรากำลังดำเนินการไปยังส่วนที่เป็นเศษส่วน:

ลองบวกศูนย์เข้ากับเศษ 4 กัน

ทีนี้หาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดลงในผลหาร:

40−40=0 เราเหลือ 0 หมายความว่าการแบ่งส่วนเสร็จสมบูรณ์แล้ว การหาร 9 ด้วย 5 จะได้เศษส่วนทศนิยม 1.8:

9: 5 = 1,8

ตัวอย่างที่ 2- หาร 84 ด้วย 5 โดยไม่มีเศษ

ขั้นแรก ให้หาร 84 ด้วย 5 ตามปกติด้วยเศษ:

เราได้ 16 อันเป็นการส่วนตัว และเหลืออีก 4 อัน ทีนี้ลองหารเศษนี้ด้วย 5 ใส่ลูกน้ำในผลหารแล้วบวก 0 เข้ากับเศษ 4

ทีนี้หาร 40 ด้วย 5 เราได้ 8 เราเขียนเลขแปดลงในผลหารหลังจุดทศนิยม:

และทำตัวอย่างให้สมบูรณ์โดยตรวจสอบว่ายังมีเศษเหลืออยู่หรือไม่:

การหารทศนิยมด้วยจำนวนปกติ

ดังที่เราทราบเศษส่วนทศนิยมประกอบด้วยจำนวนเต็มและเศษส่วน เมื่อทำการหารเศษส่วนทศนิยมด้วยจำนวนปกติ สิ่งแรกที่คุณต้องทำคือ:

• หารเศษส่วนทศนิยมทั้งหมดด้วยจำนวนนี้
• หลังจากแบ่งส่วนทั้งหมดแล้วคุณจะต้องใส่ลูกน้ำในผลหารทันทีและคำนวณต่อเช่นเดียวกับการหารปกติ

เช่น หาร 4.8 ด้วย 2

ลองเขียนตัวอย่างนี้ในมุม:

ทีนี้ลองหารทั้งหมดด้วย 2. สี่หารด้วยสองเท่ากับสอง. เราเขียนสองตัวในผลหารแล้วใส่ลูกน้ำทันที:

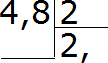
ตอนนี้เราคูณผลหารด้วยตัวหารแล้วดูว่ายังมีเศษเหลือจากการหารหรือไม่:

4−4=0 ส่วนที่เหลือเป็นศูนย์ เรายังไม่ได้เขียนเป็นศูนย์ เนื่องจากการแก้ปัญหายังไม่เสร็จสิ้น ต่อไปเราคำนวณต่อไปเหมือนการหารปกติ เอา 8 ลงมาแล้วหารด้วย 2

8: 2 = 4 เราเขียนสี่ลงในผลหารแล้วคูณด้วยตัวหารทันที:

เราได้รับคำตอบ 2.4 ค่าของนิพจน์ 4.8:2 คือ 2.4

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 8.43: 3

หาร 8 ด้วย 3 เราได้ 2 ใส่ลูกน้ำหลัง 2 ทันที:

ตอนนี้เราคูณผลหารด้วยตัวหาร 2 × 3 = 6 เราเขียนหกไว้ใต้แปดแล้วหาเศษ:

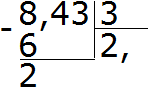
หาร 24 ด้วย 3 เราได้ 8. เราเขียน 8 ไว้ในผลหาร. คูณด้วยตัวหารทันทีเพื่อหาเศษที่เหลือของการหาร:

24−24=0 ส่วนที่เหลือเป็นศูนย์ เรายังไม่ได้เขียนลงศูนย์เลย เรานำสามตัวสุดท้ายออกจากเงินปันผลแล้วหารด้วย 3 เราจะได้ 1 คูณ 1 ด้วย 3 ทันทีเพื่อทำให้ตัวอย่างนี้สมบูรณ์:

คำตอบที่เราได้รับคือ 2.81 ซึ่งหมายความว่าค่าของนิพจน์ 8.43: 3 คือ 2.81

การหารทศนิยมด้วยทศนิยม

หากต้องการหารเศษส่วนทศนิยมด้วยเศษส่วนทศนิยม คุณต้องย้ายจุดทศนิยมในตัวหารและตัวหารไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร แล้วหารด้วยจำนวนปกติ

เช่น หาร 5.95 ด้วย 1.7

ลองเขียนนิพจน์นี้ด้วยมุม

ตอนนี้ในการจ่ายเงินปันผลและในตัวหาร เราย้ายจุดทศนิยมไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีตัวเลขหนึ่งหลักหลังจุดทศนิยม ซึ่งหมายความว่าในการจ่ายเงินปันผลและตัวหารเราต้องย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เราโอน:

หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้ว เศษส่วนทศนิยม 5.95 ก็กลายเป็นเศษส่วน 59.5 และเศษส่วนทศนิยม 1.7 หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักก็กลายเป็นเลขปกติ 17 และเรารู้วิธีหารเศษส่วนทศนิยมด้วยตัวเลขปกติแล้ว การคำนวณเพิ่มเติมไม่ใช่เรื่องยาก:

ลูกน้ำถูกย้ายไปทางขวาเพื่อให้การแบ่งง่ายขึ้น ที่อนุญาตได้เพราะเมื่อคูณหรือหารเงินปันผลและตัวหารด้วยจำนวนเดียวกัน ผลหารจะไม่เปลี่ยนแปลง มันหมายความว่าอะไร?

นี่คือหนึ่งใน คุณสมบัติที่น่าสนใจแผนก. เรียกว่าคุณสมบัติผลหาร พิจารณานิพจน์ 9: 3 = 3 หากในนิพจน์นี้เงินปันผลและตัวหารถูกคูณหรือหารด้วยจำนวนเดียวกัน ผลหาร 3 จะไม่เปลี่ยนแปลง

ลองคูณเงินปันผลและตัวหารด้วย 2 แล้วดูว่าได้อะไร:

(9 × 2) : (3 × 2) = 18: 6 = 3

ดังที่เห็นได้จากตัวอย่าง ผลหารไม่มีการเปลี่ยนแปลง

สิ่งเดียวกันนี้เกิดขึ้นเมื่อเราย้ายลูกน้ำในตัวหารและตัวหาร ในตัวอย่างก่อนหน้านี้ เราหาร 5.91 ด้วย 1.7 เราได้ย้ายเครื่องหมายจุลภาคในเงินปันผลและตัวหารไปทางขวาหนึ่งหลัก หลังจากย้ายจุดทศนิยมแล้ว เศษส่วน 5.91 ก็แปลงเป็นเศษส่วน 59.1 และเศษส่วน 1.7 ก็แปลงเป็นเลข 17 ปกติ

อันที่จริง ภายในกระบวนการนี้ มีการคูณด้วย 10 นี่คือลักษณะที่ปรากฏ:

5.91 × 10 = 59.1

ดังนั้นจำนวนหลักหลังจุดทศนิยมในตัวหารจะกำหนดว่าเงินปันผลและตัวหารจะคูณด้วยอะไร กล่าวอีกนัยหนึ่งจำนวนหลักหลังจุดทศนิยมในตัวหารจะกำหนดจำนวนหลักในการจ่ายเงินปันผลและในตัวหารจุดทศนิยมจะถูกย้ายไปทางขวา

การหารทศนิยมด้วย 10, 100, 1,000

การหารทศนิยมด้วย 10, 100 หรือ 1,000 จะทำในลักษณะเดียวกับ ตัวอย่างเช่น หาร 2.1 ด้วย 10 แก้ตัวอย่างนี้โดยใช้มุม:

แต่มีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือลูกน้ำในเงินปันผลจะถูกย้ายไปทางซ้ายตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 2.1: 10. เราดูตัวหาร. เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์หนึ่งตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 2.1 คุณต้องเลื่อนจุดทศนิยมไปทางซ้ายหนึ่งหลัก เราเลื่อนลูกน้ำไปทางซ้ายหนึ่งหลักแล้วดูว่าไม่มีหลักเหลือแล้ว ในกรณีนี้ ให้บวกศูนย์อีกตัวก่อนตัวเลข ผลลัพธ์ที่ได้คือ 0.21

ลองหาร 2.1 ด้วย 100 กัน มีศูนย์สองตัวใน 100 ซึ่งหมายความว่าในการจ่ายเงินปันผล 2.1 เราจำเป็นต้องเลื่อนลูกน้ำไปทางซ้ายสองหลัก:

2,1: 100 = 0,021

ลองหาร 2.1 ด้วย 1,000 กัน มีศูนย์สามตัวใน 1,000 ซึ่งหมายความว่าในการจ่ายเงินปันผล 2.1 คุณต้องเลื่อนลูกน้ำไปทางซ้ายสามหลัก:

2,1: 1000 = 0,0021

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001

การหารเศษส่วนทศนิยมด้วย 0.1, 0.01 และ 0.001 ก็ทำในลักษณะเดียวกับ ในการจ่ายเงินปันผลและตัวหาร คุณต้องย้ายจุดทศนิยมไปทางขวาตามหลักจำนวนเท่าที่อยู่หลังจุดทศนิยมในตัวหาร

ตัวอย่างเช่น ลองหาร 6.3 ด้วย 0.1 ก่อนอื่น ให้ย้ายเครื่องหมายจุลภาคในเงินปันผลและตัวหารไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีตัวเลขหนึ่งหลักหลังจุดทศนิยม ซึ่งหมายความว่าเราย้ายลูกน้ำในเงินปันผลและตัวหารไปทางขวาหนึ่งหลัก

หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เศษส่วนทศนิยม 6.3 จะกลายเป็นเลขปกติ 63 และเศษส่วนทศนิยม 0.1 หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักจะกลายเป็นหนึ่ง และการหาร 63 ด้วย 1 นั้นง่ายมาก:

ซึ่งหมายความว่าค่าของนิพจน์ 6.3: 0.1 คือ 63

แต่มีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือลูกน้ำในเงินปันผลจะถูกย้ายไปทางขวาตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 6.3: 0.1. ลองดูตัวหารกัน. เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์หนึ่งตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 6.3 คุณต้องเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลัก เลื่อนลูกน้ำไปทางขวาหนึ่งหลักแล้วได้ 63

ลองหาร 6.3 ด้วย 0.01 กัน ตัวหารของ 0.01 มีศูนย์สองตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 6.3 เราต้องเลื่อนจุดทศนิยมไปทางขวาสองหลัก แต่ในการจ่ายเงินปันผลจะมีเพียงหลักเดียวหลังจุดทศนิยม ในกรณีนี้ คุณต้องเพิ่มศูนย์อีกตัวที่ส่วนท้าย ผลลัพธ์ที่ได้คือ 630

ลองหาร 6.3 ด้วย 0.001 กัน ตัวหารของ 0.001 มีศูนย์สามตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 6.3 เราจำเป็นต้องเลื่อนจุดทศนิยมไปทางขวาสามหลัก:

6,3: 0,001 = 6300

งานสำหรับโซลูชันอิสระ

คุณชอบบทเรียนหรือไม่?
เข้าร่วมกับเรา กลุ่มใหม่ VKontakte และเริ่มรับการแจ้งเตือนเกี่ยวกับบทเรียนใหม่