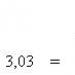بزرگترین مضرب مشترک اعداد ماشین حساب آنلاین یافتن (محاسبه) GCD و NOC

مطالب ارائه شده در زیر ادامه منطقی نظریه از مقاله تحت عنوان LCM - کمترین مضرب مشترک، تعریف، مثال ها، رابطه بین LCM و GCD است. در اینجا ما در مورد صحبت خواهیم کرد یافتن کمترین مضرب مشترک (LCM)، و به حل مثال ها توجه ویژه ای داشته باشید. اجازه دهید ابتدا نشان دهیم که چگونه LCM دو عدد بر حسب GCD این اعداد محاسبه می شود. در مرحله بعد، یافتن کمترین مضرب مشترک را با فاکتورگیری اعداد در ضرایب اول در نظر بگیرید. پس از آن بر روی یافتن LCM سه یا چند عدد تمرکز می کنیم و همچنین به محاسبه LCM اعداد منفی نیز توجه می کنیم.

پیمایش صفحه.

محاسبه کمترین مضرب مشترک (LCM) از طریق gcd

یکی از راه های یافتن کمترین مضرب مشترک بر اساس رابطه بین LCM و GCD است. رابطه موجود بین LCM و GCD به شما امکان می دهد حداقل مضرب مشترک دو عدد صحیح مثبت را از طریق بزرگترین مقسوم علیه مشترک شناخته شده محاسبه کنید. فرمول مربوطه دارای فرم است LCM(a, b)=a b: GCD(a, b) . نمونه هایی از یافتن LCM را طبق فرمول بالا در نظر بگیرید.

مثال.

کوچکترین مضرب مشترک دو عدد 126 و 70 را پیدا کنید.

راه حل.

در این مثال a=126، b=70. اجازه دهید از رابطه بین LCM و GCD که با فرمول بیان شده است استفاده کنیم LCM(a, b)=a b: GCD(a, b). یعنی ابتدا باید بزرگترین مقسوم علیه اعداد 70 و 126 را پیدا کنیم و بعد از آن می توانیم LCM این اعداد را طبق فرمول نوشته شده محاسبه کنیم.

gcd(126، 70) را با استفاده از الگوریتم اقلیدس پیدا کنید: 126=70 1+56، 70=56 1+14، 56=14 4، از این رو gcd(126، 70)=14.

اکنون حداقل مضرب مشترک مورد نیاز را پیدا می کنیم: LCM(126، 70)=126 70: GCM(126، 70)= 126 70:14=630 .

پاسخ:

LCM(126، 70)=630.

مثال.

LCM(68, 34) چیست؟

راه حل.

زیرا 68 به طور مساوی بر 34 بخش پذیر است، سپس gcd(68, 34)=34. اکنون کمترین مضرب مشترک را محاسبه می کنیم: LCM(68، 34)=68 34: LCM(68، 34)= 68 34:34=68 .

پاسخ:

LCM(68, 34)=68.

توجه داشته باشید که مثال قبلی با قانون زیر برای یافتن LCM برای اعداد صحیح مثبت a و b مطابقت دارد: اگر عدد a بر b بخش پذیر باشد، کمترین مضرب مشترک این اعداد a است.

یافتن LCM با فاکتورگیری اعداد به فاکتورهای اولیه

راه دیگر برای یافتن کمترین مضرب مشترک بر اساس فاکتورسازی اعداد به ضرایب اول است. اگر از تمام ضرایب اول این اعداد حاصل ضربی بسازیم و پس از آن همه ضرایب اول مشترکی را که در بسط این اعداد وجود دارند از این حاصلضرب حذف کنیم، حاصل ضرب حاصل برابر با کمترین مضرب مشترک این اعداد خواهد بود.

قانون اعلام شده برای یافتن LCM از برابری ناشی می شود LCM(a, b)=a b: GCD(a, b). در واقع، حاصل ضرب اعداد a و b برابر است با حاصلضرب همه عوامل دخیل در بسط اعداد a و b. به نوبه خود، gcd(a, b) برابر است با حاصلضرب همه عوامل اولی که به طور همزمان در بسط اعداد a و b وجود دارند (که در بخش یافتن gcd با استفاده از تجزیه اعداد به عوامل اول توضیح داده شده است. ).

بیایید یک مثال بزنیم. بگذارید بدانیم که 75=3 5 5 و 210=2 3 5 7 . بیایید از همه عوامل این بسط ها یک محصول بسازیم: 2 3 3 5 5 5 7 . حال تمام عواملی را که هم در بسط عدد 75 و هم در بسط عدد 210 وجود دارد را از این محصول مستثنی می کنیم (این عوامل عبارتند از 3 و 5)، سپس محصول به شکل 2 3 5 5 7 خواهد بود. مقدار این حاصلضرب برابر است با کمترین مضرب مشترک اعداد 75 و 210 یعنی LCM(75، 210)= 2 3 5 5 7 = 1 050.

مثال.

بعد از اینکه اعداد 441 و 700 را در ضرایب اول قرار دادید، کمترین مضرب مشترک این اعداد را پیدا کنید.

راه حل.

بیایید اعداد 441 و 700 را به ضرایب اول تجزیه کنیم:

441=3 3 7 7 و 700 = 2 2 5 5 7 بدست می آوریم.

حال بیایید از همه عوامل دخیل در بسط این اعداد حاصل ضرب کنیم: 2 2 3 3 5 5 7 7 7 . بگذارید همه عواملی را که به طور همزمان در هر دو بسط وجود دارند از این محصول حذف کنیم (فقط یک عامل وجود دارد - این عدد 7 است): 2 2 3 3 5 5 7 7 . به این ترتیب، LCM(441، 700)=2 2 3 3 5 5 7 7 = 44 100.

پاسخ:

LCM(441، 700)= 44 100 .

قانون یافتن LCM با استفاده از تجزیه اعداد به عوامل اول را می توان کمی متفاوت فرموله کرد. اگر عوامل گمشده از بسط عدد b را به عوامل حاصل از تجزیه عدد a اضافه کنیم، مقدار حاصلضرب برابر با کمترین مضرب مشترک اعداد a و b خواهد بود..

برای مثال، بیایید همه اعداد یکسان 75 و 210 را در نظر بگیریم، بسط آنها به ضرایب اول به شرح زیر است: 75=3 5 5 و 210=2 3 5 7 . به فاکتورهای 3، 5 و 5 از بسط عدد 75، فاکتورهای گمشده 2 و 7 را از بسط عدد 210 اضافه می کنیم، حاصل ضرب 2 3 5 5 7 را به دست می آوریم که مقدار آن LCM (75) است. ، 210).

مثال.

کوچکترین مضرب مشترک 84 و 648 را پیدا کنید.

راه حل.

ابتدا تجزیه اعداد 84 و 648 را به ضرایب اول بدست می آوریم. آنها شبیه 84=2 2 3 7 و 648=2 2 2 3 3 3 3 هستند. به فاکتورهای 2، 2، 3 و 7 از بسط عدد 84، فاکتورهای گمشده 2، 3، 3 و 3 را از بسط عدد 648 اضافه می کنیم، حاصل ضرب 2 2 2 3 3 3 3 7 را به دست می آوریم. که برابر با 4 536 است. بنابراین، حداقل مضرب مشترک مورد نظر اعداد 84 و 648، 4536 است.

پاسخ:

LCM(84، 648)=4 536.

یافتن LCM سه یا چند عدد

کمترین مضرب مشترک سه یا چند عدد را می توان با یافتن متوالی LCM دو عدد پیدا کرد. قضیه مربوطه را به یاد بیاورید که راهی برای یافتن LCM سه یا چند عدد می دهد.

قضیه.

بگذارید اعداد صحیح مثبت a 1 , a 2 , …, a k داده شوند، کمترین مضرب مشترک m k این اعداد در محاسبه ترتیبی یافت می شود m 2 = LCM (a 1 , a 2 ), m 3 = LCM (m 2 , a 3) , … , m k =LCM(m k−1 , a k) .

کاربرد این قضیه را در مثال یافتن مضرب مشترک چهار عدد در نظر بگیرید.

مثال.

LCM چهار عدد 140، 9، 54 و 250 را بیابید.

راه حل.

در این مثال 1 =140، a 2 =9، a 3 =54، a 4 =250.

ابتدا پیدا می کنیم m 2 \u003d LCM (a 1, a 2) \u003d LCM (140, 9). برای انجام این کار، با استفاده از الگوریتم اقلیدسی، gcd(140, 9) را تعیین می کنیم، 140=9 15+5، 9=5 1+4، 5=4 1+1، 4=1 4 داریم، بنابراین، gcd( 140، 9) = 1، از آنجا LCM(140، 9)=140 9: LCM(140، 9)= 140 9:1 = 1 260 . یعنی m 2 = 1 260 .

حالا پیدا می کنیم m 3 \u003d LCM (m 2, a 3) \u003d LCM (1 260, 54). بیایید آن را از طریق gcd(1 260, 54) محاسبه کنیم که توسط الگوریتم اقلیدس نیز تعیین می شود: 1 260=54 23+18 , 54=18 3 . سپس gcd(1 260, 54)=18، از آنجا LCM(1 260, 54)= 1 260 54:gcd(1 260, 54)= 1 260 54:18=3 780 . یعنی m 3 \u003d 3 780.

چپ برای پیدا کردن m 4 \u003d LCM (m 3, a 4) \u003d LCM (3 780, 250). برای انجام این کار، GCD(3 780, 250) را با استفاده از الگوریتم اقلیدس پیدا می کنیم: 3 780=250 15+30 , 250=30 8+10 , 30=10 3 . بنابراین، gcd(3 780، 250) = 10، از آنجا gcd (3 780، 250) = 3 780 250:gcd(3 780، 250)= 3 780 250:10=94 500 . یعنی m 4 \u003d 94 500.

بنابراین کمترین مضرب مشترک چهار عدد اصلی 94500 است.

پاسخ:

LCM(140, 9, 54, 250)=94,500.

در بسیاری از موارد، کمترین مضرب مشترک سه یا چند اعداد به راحتی با استفاده از فاکتورسازی اول اعداد داده شده پیدا می شود. در این صورت باید از قانون زیر پیروی کرد. کمترین مضرب مشترک چند عدد برابر حاصل ضرب است که به صورت زیر تشکیل می شود: عوامل گمشده از بسط عدد دوم به همه عوامل از بسط عدد اول اضافه می شوند، عوامل مفقود از بسط عدد اول. عدد سوم به فاکتورهای بدست آمده اضافه می شود و غیره.

مثالی از یافتن کمترین مضرب مشترک با استفاده از تجزیه اعداد به عوامل اول را در نظر بگیرید.

مثال.

کوچکترین مضرب مشترک پنج عدد 84، 6، 48، 7، 143 را بیابید.

راه حل.

ابتدا بسط های این اعداد را به ضرایب اول به دست می آوریم: 84=2 2 3 7 , 6=2 3 , 48=2 2 2 2 3 , 7 عامل اول) و 143=11 13 .

برای یافتن LCM این اعداد، به فاکتورهای عدد اول 84 (آنها 2، 2، 3 و 7 هستند) باید فاکتورهای گمشده از بسط عدد دوم 6 را اضافه کنید. بسط عدد 6 شامل عوامل گمشده نیست، زیرا هر دو و 3 در بسط اولین عدد 84 وجود دارند. علاوه بر فاکتورهای 2، 2، 3 و 7، فاکتورهای گمشده 2 و 2 را از بسط عدد سوم 48 جمع می کنیم، مجموعه ای از عوامل 2، 2، 2، 2، 3 و 7 را به دست می آوریم. نیازی به افزودن فاکتورها به این مجموعه در مرحله بعد نیست، زیرا 7 قبلاً در آن موجود است. در نهایت به فاکتورهای 2، 2، 2، 2، 3 و 7 فاکتورهای گمشده 11 و 13 را از بسط عدد 143 اضافه می کنیم. حاصلضرب 2 2 2 2 3 7 11 13 را بدست می آوریم که برابر با 48 048 است.

اما بسیاری از اعداد طبیعی به طور مساوی بر سایر اعداد طبیعی بخش پذیرند.

مثلا:

عدد 12 بر 1، بر 2، بر 3، بر 4، بر 6، بر 12 بخش پذیر است.

عدد 36 بر 1، بر 2، بر 3، بر 4، بر 6، بر 12، بر 18، بر 36 بخش پذیر است.

اعدادی که عدد بر آنها بخش پذیر است (برای 12 عدد 1، 2، 3، 4، 6 و 12 است) نامیده می شوند. مقسوم علیه اعداد. مقسوم علیه یک عدد طبیعی آعدد طبیعی است که عدد داده شده را تقسیم می کند آبدون هیچ ردی. عدد طبیعی که بیش از دو عامل داشته باشد نامیده می شود کامپوزیت .

توجه داشته باشید که اعداد 12 و 36 مقسوم علیه مشترک دارند. این اعداد عبارتند از: 1، 2، 3، 4، 6، 12. بزرگترین مقسوم علیه این اعداد 12 است. مقسوم علیه مشترک این دو عدد آو بعددی است که هر دو عدد داده شده بدون باقیمانده بر آن بخش پذیرند آو ب.

مضرب مشترکچند عدد به عددی گفته می شود که بر هر یک از این اعداد بخش پذیر باشد. مثلا، اعداد 9، 18 و 45 مضرب مشترک 180 دارند. اما 90 و 360 نیز مضرب مشترک آنها هستند. در بین همه مضربهای jcommon، همیشه کوچکترین آنها وجود دارد، در این مورد 90 است. این عدد نامیده می شود. کمترینمضرب مشترک (LCM).

LCM همیشه یک عدد طبیعی است که باید بزرگتر از بزرگترین اعدادی باشد که برای آن تعریف شده است.

حداقل مضرب مشترک (LCM). خواص.

جابجایی:

انجمنی:

به طور خاص، اگر و اعداد هم اول باشند، پس:

حداقل مضرب مشترک دو عدد صحیح مترو nمقسوم علیه همه مضرب های مشترک دیگر است مترو n. علاوه بر این، مجموعه ای از مضرب های مشترک m,nمنطبق با مجموعه مضرب برای LCM( m,n).

مجانبی برای را می توان در قالب برخی از توابع نظری اعداد بیان کرد.

بنابراین، عملکرد چبیشف. همچنین:

این از تعریف و ویژگی های تابع لاندو به دست می آید g(n).

آنچه از قانون توزیع اعداد اول به دست می آید.

یافتن حداقل مضرب مشترک (LCM).

NOC( الف، ب) به چند روش قابل محاسبه است:

1. اگر بزرگترین مقسوم علیه مشترک شناخته شده است، می توانید از رابطه آن با LCM استفاده کنید:

2. اجازه دهید تجزیه متعارف هر دو عدد به عوامل اول مشخص شود:

جایی که p 1,...,p kاعداد اول مختلف هستند و d 1،...،d kو e 1,...,ekاعداد صحیح غیر منفی هستند (اگر عدد اول مربوطه در بسط نباشد، می توانند صفر باشند).

سپس LCM ( آ,ب) با فرمول محاسبه می شود:

به عبارت دیگر، بسط LCM شامل تمام عوامل اولی است که حداقل در یکی از بسط های اعداد گنجانده شده است. الف، ب، و بزرگترین از دو شاخص این عامل گرفته شده است.

مثال:

محاسبه کمترین مضرب مشترک چند عدد را می توان به چندین محاسبه متوالی LCM دو عدد تقلیل داد:

قانون.برای پیدا کردن LCM یک سری اعداد، شما نیاز دارید:

- اعداد را به عوامل اول تجزیه کنید.

- بزرگترین انبساط را به فاکتورهای حاصلضرب مورد نظر (محصول ضرایب بیشترین تعداد داده شده) منتقل کنید و سپس عواملی را از بسط اعداد دیگری که در عدد اول رخ نمی دهند یا در آن هستند اضافه کنید. تعداد دفعات کمتر؛

- حاصل ضرب ضرایب اول LCM اعداد داده شده خواهد بود.

هر دو یا چند عدد طبیعی LCM خود را دارند. اگر اعداد مضرب یکدیگر نباشند یا عوامل یکسانی در بسط نداشته باشند، LCM آنها برابر است با حاصلضرب این اعداد.

ضرایب اول عدد 28 (2، 2، 7) با ضریب 3 (عدد 21) تکمیل شد، حاصلضرب حاصل (84) کوچکترین عددی خواهد بود که بر 21 و 28 بخش پذیر است.

ضرایب اول بزرگترین عدد 30 با ضریب 5 از عدد 25 تکمیل شد، حاصل ضرب 150 بزرگتر از بزرگترین عدد 30 است و بر همه اعداد داده شده بدون باقیمانده بخش پذیر است. این کوچکترین حاصل ضرب ممکن (150، 250، 300...) است که همه اعداد داده شده مضرب آن هستند.

اعداد 2،3،11،37 اول هستند، بنابراین LCM آنها برابر است با حاصلضرب اعداد داده شده.

قانون. برای محاسبه LCM اعداد اول، باید همه این اعداد را در هم ضرب کنید.

گزینه ای دیگر:

برای یافتن کمترین مضرب مشترک (LCM) از چندین عدد به موارد زیر نیاز دارید:

1) هر عدد را به عنوان حاصلضرب عوامل اول آن نشان دهید، برای مثال:

504 \u003d 2 2 2 3 3 7،

2) توان همه عوامل اول را بنویسید:

504 \u003d 2 2 2 3 3 7 \u003d 2 3 3 2 7 1,

3) تمام مقسوم علیه های اول (ضرب) هر یک از این اعداد را بنویسید.

4) بزرگترین درجه هر یک از آنها را که در همه بسط های این اعداد یافت می شود انتخاب کنید.

5) این قدرت ها را چند برابر کنید.

مثال. LCM اعداد: 168، 180 و 3024 را بیابید.

راه حل. 168 \u003d 2 2 2 3 7 \u003d 2 3 3 1 7 1,

180 \u003d 2 2 3 3 5 \u003d 2 2 3 2 5 1,

3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1 .

ما بزرگترین قدرت های همه مقسوم علیه های اول را می نویسیم و آنها را ضرب می کنیم:

LCM = 2 4 3 3 5 1 7 1 = 15120.

شماره دوم: b=

جداکننده رقمبدون جداکننده فضا "'

نتیجه:

بزرگترین مقسوم علیه gcd( آ,ب)=6

کمترین مضرب مشترک LCM( آ,ب)=468

بزرگترین عدد طبیعی که اعداد a و b بدون باقیمانده بر آن بخش پذیرند نامیده می شود بزرگترین مقسوم علیه مشترک(gcd) از این اعداد. به gcd(a,b), (a,b), gcd(a,b) یا hcf(a,b) نشان داده شده است.

کمترین مضرب مشترک(LCM) از دو عدد صحیح a و b کوچکترین عدد طبیعی است که بدون باقیمانده بر a و b بخش پذیر است. LCM(a,b) یا lcm(a,b) نشان داده می شود.

اعداد صحیح a و b نامیده می شوند coprimeاگر هیچ مقسوم علیه مشترک دیگری به جز +1 و -1 نداشته باشند.

بزرگترین مقسوم علیه مشترک

بگذارید دو عدد مثبت داده شود آ 1 و آ 2 1). لازم است یک مقسوم علیه مشترک این اعداد پیدا شود، یعنی. چنین عددی را پیدا کنید λ ، که اعداد را تقسیم می کند آ 1 و آ 2 به طور همزمان. بیایید الگوریتم را شرح دهیم.

1) در این مقاله کلمه عدد به معنای یک عدد صحیح خواهد بود.

اجازه دهید آ 1 ≥ آ 2 و اجازه دهید

جایی که متر 1 , آ 3 تعدادی اعداد صحیح هستند، آ 3 <آ 2 (باقی مانده از تقسیم آ 1 در آ 2 باید کمتر باشد آ 2).

بیایید وانمود کنیم که λ تقسیم می کند آ 1 و آ 2، سپس λ تقسیم می کند متر 1 آ 2 و λ تقسیم می کند آ 1 −متر 1 آ 2 =آ 3 (اظهار 2 از مقاله «تقسیم پذیری اعداد. علامت تقسیم پذیری»). نتیجه می شود که هر مقسوم علیه مشترک آ 1 و آ 2 یک مقسوم علیه مشترک است آ 2 و آ 3 . عکس آن نیز صادق است اگر λ مقسوم علیه مشترک آ 2 و آ 3، سپس متر 1 آ 2 و آ 1 =متر 1 آ 2 +آ 3 نیز به تقسیم می شوند λ . از این رو مقسوم علیه مشترک است آ 2 و آ 3 نیز یک مقسوم علیه مشترک است آ 1 و آ 2. زیرا آ 3 <آ 2 ≤آ 1، پس می توان گفت که حل مسئله یافتن مقسوم علیه مشترک اعداد است آ 1 و آ 2 به یک مسئله ساده تر یعنی یافتن مقسوم علیه مشترک اعداد کاهش می یابد آ 2 و آ 3 .

اگر یک آ 3 ≠0، سپس می توانیم تقسیم کنیم آ 2 در آ 3 . سپس

,

جایی که متر 1 و آ 4 تعدادی اعداد صحیح هستند، ( آ 4 باقی مانده از تقسیم آ 2 در آ 3 (آ 4 <آ 3)). با استدلال مشابه به این نتیجه می رسیم که مقسوم علیه های مشترک اعداد آ 3 و آ 4 همان مقسوم علیه مشترک اعداد است آ 2 و آ 3 و همچنین با مقسوم علیه های مشترک آ 1 و آ 2. زیرا آ 1 , آ 2 , آ 3 , آ 4، ... اعدادی که دائما در حال کاهش هستند و از آنجایی که تعداد محدودی از اعداد صحیح بین آنها وجود دارد. آ 2 و 0، سپس در مرحله ای n، باقی مانده تقسیم آغیر آ n+1 برابر با صفر خواهد بود ( آ n+2=0).

.

هر مقسوم علیه مشترک λ شماره آ 1 و آ 2 نیز مقسوم علیه اعداد است آ 2 و آ 3 , آ 3 و آ 4 , .... آ n و آ n+1 . برعکس نیز درست است، مقسوم علیه مشترک اعداد آ n و آ n+1 نیز مقسوم علیه اعداد هستند آ n-1 و آ n، ....، آ 2 و آ 3 , آ 1 و آ 2. اما مقسوم علیه مشترک آ n و آ n+1 یک عدد است آ n+1، زیرا آ n و آ n+1 بر بخش پذیر هستند آ n+1 (به یاد بیاورید آ n+2=0). در نتیجه آ n+1 نیز مقسوم علیه اعداد است آ 1 و آ 2 .

توجه داشته باشید که شماره آ n+1 بزرگترین مقسوم علیه اعداد است آ n و آ n+1 از بزرگترین مقسوم علیه آ n+1 خودش است آ n+1 . اگر یک آ n + 1 را می توان به عنوان حاصلضرب اعداد صحیح نشان داد، سپس این اعداد نیز مقسوم علیه مشترک اعداد هستند. آ 1 و آ 2. عدد آ n+1 نامیده می شوند بزرگترین مقسوم علیه مشترکشماره آ 1 و آ 2 .

شماره آ 1 و آ 2 می تواند اعداد مثبت و منفی باشد. اگر یکی از اعداد برابر با صفر باشد، بزرگترین مقسوم علیه مشترک این اعداد برابر با قدر مطلق عدد دیگر خواهد بود. بزرگترین مقسوم علیه مشترک اعداد صفر تعریف نشده است.

الگوریتم فوق نامیده می شود الگوریتم اقلیدسبرای پیدا کردن بزرگترین مقسوم علیه مشترک دو عدد صحیح.

مثالی از یافتن بزرگترین مقسوم علیه مشترک دو عدد

بزرگترین مقسوم علیه مشترک دو عدد 630 و 434 را پیدا کنید.

• مرحله 1. عدد 630 را بر 434 تقسیم کنید. باقیمانده 196 است.
• مرحله 2. عدد 434 را بر 196 تقسیم کنید. باقیمانده 42 است.
• مرحله 3. عدد 196 را بر 42 تقسیم کنید. باقیمانده 28 است.
• مرحله 4. عدد 42 را بر 28 تقسیم کنید باقیمانده 14 است.
• مرحله 5. عدد 28 را بر 14 تقسیم کنید، باقیمانده 0 است.

در مرحله 5 باقیمانده تقسیم 0 است.بنابراین بزرگترین مقسوم علیه اعداد 630 و 434 14 است. توجه داشته باشید که اعداد 2 و 7 نیز مقسوم علیه اعداد 630 و 434 هستند.

اعداد همزمان اول

تعریف 1. بزرگترین مقسوم علیه مشترک اعداد را بگذارید آ 1 و آ 2 برابر با یک است. سپس این اعداد فراخوانی می شوند اعداد همزمان اولکه مقسوم علیه مشترک ندارند.

قضیه 1. اگر یک آ 1 و آ 2 عدد نسبتا اول و λ یک عدد، سپس هر مقسوم علیه مشترک اعداد λa 1 و آ 2 نیز مقسوم علیه مشترک اعداد است λ و آ 2 .

اثبات الگوریتم اقلیدس را برای یافتن بزرگترین مقسوم علیه مشترک اعداد در نظر بگیرید آ 1 و آ 2 (به بالا مراجعه کنید).

.

از شرایط قضیه برمی آید که بزرگترین مقسوم علیه مشترک اعداد آ 1 و آ 2، و بنابراین آ n و آ n+1 برابر با 1 است. آ n+1=1.

بیایید همه این برابری ها را در ضرب کنیم λ ، سپس

.

اجازه دهید مقسوم علیه مشترک آ 1 λ و آ 2 است δ . سپس δ به عنوان یک عامل وارد می شود آ 1 λ , متر 1 آ 2 λ و در آ 1 λ -متر 1 آ 2 λ =آ 3 λ (به "تقسیم پذیری اعداد"، بیانیه 2 مراجعه کنید). به علاوه δ به عنوان یک عامل وارد می شود آ 2 λ و متر 2 آ 3 λ ، و از این رو به عنوان یک عامل وارد می شود آ 2 λ -متر 2 آ 3 λ =آ 4 λ .

با استدلال به این روش، ما متقاعد می شویم که δ به عنوان یک عامل وارد می شود آ n-1 λ و متر n-1 آ n λ ، و بنابراین در آ n-1 λ −متر n-1 آ n λ =آ n+1 λ . زیرا آ n+1 =1، سپس δ به عنوان یک عامل وارد می شود λ . از این رو شماره δ مقسوم علیه مشترک اعداد است λ و آ 2 .

موارد خاص قضیه 1 را در نظر بگیرید.

نتیجه 1. اجازه دهید آو جاعداد اول نسبتا هستند ب. سپس محصول آنها acیک عدد اول نسبت به ب.

واقعا از قضیه 1 acو بدارای مقسوم علیه های مشترک مشابه هستند جو ب. اما اعداد جو ب coprime، یعنی دارای یک مقسوم علیه مشترک 1. سپس acو بهمچنین دارای یک مقسوم علیه مشترک 1. از این رو acو بمتقابل ساده

نتیجه 2. اجازه دهید آو باعداد coprime و let بتقسیم می کند ak. سپس بتقسیم می کند و ک.

واقعا از شرط ادعا akو بمقسوم علیه مشترک دارند ب. به موجب قضیه 1، بباید مقسوم علیه مشترک باشد بو ک. در نتیجه بتقسیم می کند ک.

نتیجه 1 را می توان تعمیم داد.

نتیجه 3. 1. اجازه دهید اعداد آ 1 , آ 2 , آ 3 , ..., آ m نسبت به عدد اول هستند ب. سپس آ 1 آ 2 , آ 1 آ 2 · آ 3 , ..., آ 1 آ 2 آ 3 ··· آ m، حاصل ضرب این اعداد نسبت به عدد اول است ب.

2. اجازه دهید دو ردیف اعداد داشته باشیم

به طوری که هر عدد در ردیف اول نسبت به هر عدد در ردیف دوم اول باشد. سپس محصول

یافتن چنین اعدادی که بر هر یک از این اعداد بخش پذیر باشند لازم است.

اگر عدد بر آن بخش پذیر باشد آ 1، سپس به نظر می رسد sa 1، کجا ستعدادی عدد اگر یک qبزرگترین مقسوم علیه مشترک اعداد است آ 1 و آ 2، سپس

جایی که س 1 مقداری عدد صحیح است. سپس

است حداقل مضرب مشترک اعداد آ 1 و آ 2 .

آ 1 و آ 2 هم اول، سپس کمترین مضرب مشترک اعداد آ 1 و آ 2:

کمترین مضرب مشترک این اعداد را پیدا کنید.

از موارد فوق نتیجه می گیرد که هر مضربی از اعداد آ 1 , آ 2 , آ 3 باید مضربی از اعداد باشد ε و آ 3 و بالعکس. حداقل مضرب مشترک اعداد را بگذارید ε و آ 3 است ε یکی . علاوه بر این، مضربی از اعداد آ 1 , آ 2 , آ 3 , آ 4 باید مضربی از اعداد باشد ε 1 و آچهار . حداقل مضرب مشترک اعداد را بگذارید ε 1 و آ 4 است ε 2. بنابراین، ما متوجه شدیم که همه مضرب اعداد آ 1 , آ 2 , آ 3 ,...,آ m منطبق بر مضرب یک عدد خاص است ε n که کمترین مضرب مشترک اعداد داده شده نامیده می شود.

در مورد خاص زمانی که اعداد آ 1 , آ 2 , آ 3 ,...,آ m coprime، سپس کمترین مضرب مشترک اعداد آ 1 , آ 2 همانطور که در بالا نشان داده شده است شکل (3) دارد. علاوه بر این، از آن زمان آ 3 عدد اول نسبت به اعداد آ 1 , آ 2، سپس آ 3 یک عدد نسبی اول است آیک · آ 2 (نتیجه 1). بنابراین کمترین مضرب مشترک اعداد آ 1 ,آ 2 ,آ 3 یک عدد است آیک · آ 2 · آ 3 . با استدلالی مشابه، به ادعاهای زیر می رسیم.

بیانیه 1. کمترین مضرب مشترک اعداد هم اول آ 1 , آ 2 , آ 3 ,...,آ m برابر حاصلضرب آنهاست آیک · آ 2 · آ 3 ··· آمتر

بیانیه 2. هر عددی که بر هر یک از اعداد همزمان اول بخش پذیر باشد آ 1 , آ 2 , آ 3 ,...,آ m نیز بر حاصلضرب آنها قابل تقسیم است آیک · آ 2 · آ 3 ··· آمتر

سه راه برای یافتن کمترین مضرب مشترک در نظر بگیرید.

یافتن با فاکتورینگ

راه اول یافتن کمترین مضرب مشترک با فاکتورگیری اعداد داده شده در ضرایب اول است.

فرض کنید باید LCM اعداد: 99، 30 و 28 را پیدا کنیم. برای این کار، هر یک از این اعداد را به عوامل اول تجزیه می کنیم:

برای اینکه عدد مورد نظر بر 99، 30 و 28 بخش پذیر باشد، لازم و کافی است که شامل تمام ضرایب اول این مقسوم علیه ها باشد. برای انجام این کار، باید همه ضرایب اول این اعداد را به بالاترین توان وقوع برسانیم و آنها را با هم ضرب کنیم:

2 2 3 2 5 7 11 = 13 860

بنابراین LCM (99، 30، 28) = 13860. هیچ عدد دیگری کمتر از 13860 به طور مساوی بر 99، 30 یا 28 بخش پذیر نیست.

برای یافتن کمترین مضرب مشترک اعداد داده شده، باید آنها را در ضرایب اول قرار دهید، سپس هر عامل اول را با بزرگترین توانی که رخ می دهد، بگیرید و این عوامل را در هم ضرب کنید.

از آنجایی که اعداد همزمان اول هیچ عامل اول مشترکی ندارند، حداقل مضرب مشترک آنها برابر با حاصلضرب این اعداد است. به عنوان مثال، سه عدد: 20، 49 و 33 هم اول هستند. از همین رو

LCM (20، 49، 33) = 20 49 33 = 32،340.

هنگام جستجوی کمترین مضرب مشترک اعداد اول مختلف نیز باید همین کار را کرد. به عنوان مثال، LCM (3، 7، 11) = 3 7 11 = 231.

یافتن با انتخاب

راه دوم یافتن کمترین مضرب مشترک با برازش است.

مثال 1. وقتی بزرگترین اعداد داده شده به طور مساوی بر اعداد داده شده دیگر بخش پذیر باشد، LCM این اعداد برابر است با بزرگتر آنها. به عنوان مثال، چهار عدد 60، 30، 10 و 6 داده می شود. هر یک از آنها بر 60 بخش پذیر است، بنابراین:

NOC(60، 30، 10، 6) = 60

در موارد دیگر، برای یافتن کمترین مضرب مشترک، از روش زیر استفاده می شود:

1. بزرگترین عدد را از اعداد داده شده تعیین کنید.
2. در مرحله بعد، اعدادی را می یابیم که مضرب بزرگترین عدد هستند، آن را در اعداد طبیعی به ترتیب صعودی ضرب می کنیم و بررسی می کنیم که آیا اعداد داده شده باقیمانده بر حاصلضرب تقسیم می شوند یا خیر.

مثال 2. با توجه به سه عدد 24، 3 و 18. بزرگترین آنها را تعیین کنید - این عدد 24 است. سپس، اعداد مضرب 24 را پیدا کنید و بررسی کنید که آیا هر یک از آنها بر 18 و بر 3 بخش پذیر است یا خیر:

24 1 = 24 بر 3 بخش پذیر است اما بر 18 بخش پذیر نیست.

24 2 = 48 - قابل تقسیم بر 3 اما بر 18 بخش پذیر نیست.

24 3 \u003d 72 - قابل تقسیم بر 3 و 18.

بنابراین LCM(24، 3، 18) = 72.

یافتن با یافتن متوالی LCM

راه سوم یافتن کمترین مضرب مشترک با یافتن متوالی LCM است.

LCM دو عدد داده شده برابر است با حاصلضرب این اعداد تقسیم بر بزرگترین مقسوم علیه مشترکشان.

مثال 1. LCM دو عدد داده شده را بیابید: 12 و 8. بزرگترین مقسوم علیه مشترک آنها را تعیین کنید: GCD (12، 8) = 4. این اعداد را ضرب کنید:

ما محصول را به GCD آنها تقسیم می کنیم:

بنابراین LCM(12، 8) = 24.

برای یافتن LCM سه یا چند عدد از روش زیر استفاده می شود:

1. ابتدا LCM هر دو عدد از داده ها پیدا می شود.
2. سپس، LCM حداقل مضرب مشترک پیدا شده و سومین عدد داده شده.
3. سپس، LCM حاصل از حداقل مضرب مشترک و عدد چهارم، و غیره.
4. بنابراین جستجوی LCM تا زمانی که اعداد وجود دارد ادامه می یابد.

مثال 2. بیایید LCM سه عدد داده شده را پیدا کنیم: 12، 8 و 9. قبلاً LCM اعداد 12 و 8 را در مثال قبلی پیدا کرده ایم (این عدد 24 است). باقی مانده است که کوچکترین مضرب مشترک 24 و سومین عدد داده شده - 9 را پیدا کنیم. بزرگترین مقسوم علیه مشترک آنها را تعیین کنید: gcd (24, 9) = 3. LCM را با عدد 9 ضرب کنید:

ما محصول را به GCD آنها تقسیم می کنیم:

بنابراین LCM(12، 8، 9) = 72.

بیایید بحث را در مورد کمترین مضرب مشترک که در بخش LCM - کمترین مضرب مشترک، تعریف، مثال شروع کردیم، ادامه دهیم. در این مبحث به روش هایی برای یافتن LCM برای سه عدد یا بیشتر می پردازیم، این سوال را تجزیه و تحلیل خواهیم کرد که چگونه LCM یک عدد منفی را پیدا کنیم.

Yandex.RTB R-A-339285-1

محاسبه کمترین مضرب مشترک (LCM) از طریق gcd

ما قبلاً رابطه بین کمترین مضرب مشترک و بزرگترین مقسوم علیه مشترک را ایجاد کرده ایم. حالا بیایید یاد بگیریم که چگونه LCM را از طریق GCD تعریف کنیم. ابتدا بیایید بفهمیم که چگونه این کار را برای اعداد مثبت انجام دهیم.

تعریف 1

با استفاده از فرمول LCM (a, b) \u003d a b: GCD (a, b) می توانید کمترین مضرب مشترک را از طریق بزرگترین مقسوم علیه مشترک پیدا کنید.

مثال 1

باید LCM اعداد 126 و 70 را پیدا کرد.

راه حل

بیایید a = 126، b = 70 را در نظر بگیریم. مقادیر موجود در فرمول را برای محاسبه کمترین مضرب مشترک از طریق بزرگترین مقسوم علیه مشترک LCM (a, b) = a · b: GCD (a, b) جایگزین کنید.

GCD اعداد 70 و 126 را پیدا می کند. برای این ما به الگوریتم اقلیدس نیاز داریم: 126 = 70 1 + 56 , 70 = 56 1 + 14 , 56 = 14 4 , از این رو gcd (126 , 70) = 14 .

بیایید LCM را محاسبه کنیم: LCM (126، 70) = 126 70: GCD (126، 70) = 126 70: 14 = 630.

پاسخ: LCM (126، 70) = 630.

مثال 2

نوک اعداد 68 و 34 را پیدا کنید.

راه حل

یافتن GCD در این مورد آسان است، زیرا 68 بر 34 بخش پذیر است. حداقل مضرب مشترک را با استفاده از فرمول محاسبه کنید: LCM (68، 34) = 68 34: GCD (68، 34) = 68 34: 34 = 68.

پاسخ: LCM(68، 34) = 68.

در این مثال از قانون یافتن حداقل مضرب مشترک اعداد صحیح مثبت a و b استفاده کردیم: اگر عدد اول بر دوم بخش پذیر باشد، LCM این اعداد برابر با عدد اول خواهد بود.

یافتن LCM با فاکتورگیری اعداد به فاکتورهای اولیه

حال بیایید به راهی برای یافتن LCM نگاه کنیم که بر اساس تجزیه اعداد به عوامل اول است.

تعریف 2

برای یافتن کمترین مضرب مشترک، باید چند مرحله ساده را انجام دهیم:

• ما حاصل ضرب همه ضرایب اول اعدادی را که برای آنها باید LCM را پیدا کنیم، تشکیل می دهیم.
• ما همه عوامل اصلی را از محصولات به دست آمده آنها حذف می کنیم.
• حاصلضرب پس از حذف ضرایب اول مشترک برابر با LCM اعداد داده شده خواهد بود.

این روش برای یافتن کمترین مضرب مشترک بر اساس برابری LCM (a , b) = a b: GCD (a , b) است. اگر به فرمول نگاه کنید، مشخص می شود: حاصل ضرب اعداد a و b برابر است با حاصلضرب همه عواملی که در بسط این دو عدد نقش دارند. در این حالت، GCD دو عدد برابر است با حاصلضرب تمام عوامل اولی که همزمان در فاکتورگیری این دو عدد وجود دارند.

مثال 3

ما دو عدد 75 و 210 داریم. ما می توانیم آنها را به صورت زیر در نظر بگیریم: 75 = 3 5 5و 210 = 2 3 5 7. اگر حاصل ضرب همه ضرایب دو عدد اصلی را بسازید، به دست می آورید: 2 3 3 5 5 5 7.

اگر عوامل مشترک هر دو عدد 3 و 5 را حذف کنیم، حاصلضرب شکل زیر به دست می آید: 2 3 5 5 7 = 1050. این محصول LCM ما برای اعداد 75 و 210 خواهد بود.

مثال 4

LCM اعداد را پیدا کنید 441 و 700 ، هر دو عدد را به عوامل اول تجزیه می کند.

راه حل

بیایید همه عوامل اول اعداد داده شده در شرط را پیدا کنیم:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

دو زنجیره اعداد بدست می آوریم: 441 = 3 3 7 7 و 700 = 2 2 5 5 7 .

حاصلضرب تمام عواملی که در گسترش این اعداد مشارکت داشته اند به صورت زیر خواهد بود: 2 2 3 3 5 5 7 7 7. بیایید عوامل مشترک را پیدا کنیم. این عدد 7 است. ما آن را از محصول کلی حذف می کنیم: 2 2 3 3 5 5 7 7. معلوم می شود که NOC (441، 700) = 2 2 3 3 5 5 7 7 = 44 100.

پاسخ: LCM (441، 700) = 44 100.

اجازه دهید یک فرمول دیگر از روش برای یافتن LCM با تجزیه اعداد به عوامل اول ارائه دهیم.

تعریف 3

قبلاً، ما از تعداد کل عوامل مشترک برای هر دو عدد حذف شدیم. حالا ما این کار را متفاوت انجام خواهیم داد:

• بیایید هر دو عدد را به عوامل اول تجزیه کنیم:
• به حاصل ضرب ضرایب اول عدد اول عوامل گمشده عدد دوم را اضافه کنید.
• حاصلضرب را بدست می آوریم که LCM مورد نظر دو عددی خواهد بود.

مثال 5

بیایید به اعداد 75 و 210 برگردیم که قبلاً در یکی از نمونه‌های قبلی به دنبال LCM بودیم. بیایید آنها را به عوامل ساده تقسیم کنیم: 75 = 3 5 5و 210 = 2 3 5 7. به حاصل ضرب عوامل 3، 5 و 5 شماره 75 فاکتورهای گمشده را اضافه کنید 2 و 7 اعداد 210 . ما گرفتیم: 2 3 5 5 7 .این LCM اعداد 75 و 210 است.

مثال 6

محاسبه LCM اعداد 84 و 648 ضروری است.

راه حل

بیایید اعداد را از شرط به عوامل اول تجزیه کنیم: 84 = 2 2 3 7و 648 = 2 2 2 3 3 3 3. به حاصل ضرب عوامل 2، 2، 3 و 7 اعداد 84 عوامل گمشده 2، 3، 3 و
3 شماره های 648 . ما محصول را دریافت می کنیم 2 2 2 3 3 3 3 7 = 4536 .این کمترین مضرب مشترک 84 و 648 است.

پاسخ: LCM (84، 648) = 4536.

یافتن LCM سه یا چند عدد

صرف نظر از اینکه با چه تعداد اعداد سروکار داریم، الگوریتم اقدامات ما همیشه یکسان خواهد بود: ما به صورت متوالی LCM دو عدد را پیدا خواهیم کرد. یک قضیه برای این مورد وجود دارد.

قضیه 1

فرض کنید اعداد صحیح داریم a 1 , a 2 , … , a k. NOC m kاز این اعداد در محاسبه ترتیبی m 2 = LCM (a 1 , a 2 ) , m 3 = LCM (m 2 , a 3 ) , … , m k = LCM (m k − 1 , a k) یافت می شود.

حال بیایید ببینیم که چگونه می توان این قضیه را برای مسائل خاص اعمال کرد.

مثال 7

شما باید حداقل مضرب مشترک چهار عدد 140، 9، 54 و را محاسبه کنید 250 .

راه حل

بیایید نماد را معرفی کنیم: a 1 \u003d 140 ، a 2 \u003d 9 ، a 3 \u003d 54 ، a 4 \u003d 250.

بیایید با محاسبه m 2 = LCM (a 1 , a 2) = LCM (140 , 9) شروع کنیم. بیایید از الگوریتم اقلیدسی برای محاسبه GCD اعداد 140 و 9 استفاده کنیم: 140 = 9 15 + 5 , 9 = 5 1 + 4 , 5 = 4 1 + 1 , 4 = 1 4 . دریافت می کنیم: GCD(140، 9) = 1، LCM(140، 9) = 140 9: GCD(140، 9) = 140 9: 1 = 1260. بنابراین، m 2 = 1 260 .

حالا بیایید طبق همان الگوریتم محاسبه کنیم m 3 = LCM (m 2 , a 3) = LCM (1 260 , 54). در طول محاسبات، m 3 = 3 780 بدست می آوریم.

باقی مانده است که m 4 \u003d LCM (m 3, a 4) \u003d LCM (3 780, 250) محاسبه کنیم. ما طبق همان الگوریتم عمل می کنیم. m 4 \u003d 94 500 دریافت می کنیم.

LCM چهار عدد از شرط مثال 94500 است.

پاسخ: LCM (140، 9، 54، 250) = 94500.

همانطور که می بینید، محاسبات ساده، اما بسیار پر زحمت هستند. برای صرفه جویی در زمان، می توانید از راه دیگری بروید.

تعریف 4

ما الگوریتم اقدامات زیر را به شما پیشنهاد می کنیم:

• همه اعداد را به عوامل اول تجزیه کنید.
• به حاصل ضرب ضرایب عدد اول، عوامل گمشده را از حاصل ضرب عدد دوم اضافه کنید.
• فاکتورهای گمشده عدد سوم را به محصول به دست آمده در مرحله قبل و غیره اضافه کنید.
• حاصلضرب حاصل حداقل مضرب مشترک همه اعداد شرط خواهد بود.

مثال 8

لازم است LCM پنج عدد 84، 6، 48، 7، 143 را پیدا کنید.

راه حل

بیایید هر پنج عدد را به عوامل اول تجزیه کنیم: 84 = 2 2 3 7 , 6 = 2 3 , 48 = 2 2 2 2 3 , 7 , 143 = 11 13 . اعداد اول که عدد 7 است را نمی توان در فاکتورهای اول قرار داد. چنین اعدادی با تجزیه آنها به عوامل اول همزمان است.

حالا حاصل ضرب ضرایب اول 2، 2، 3 و 7 عدد 84 را گرفته و ضرایب گمشده عدد دوم را به آنها اضافه می کنیم. عدد 6 را به 2 و 3 تبدیل کرده ایم. این عوامل قبلاً در حاصل ضرب عدد اول هستند. بنابراین، آنها را حذف می کنیم.

ما به اضافه کردن ضریب های گمشده ادامه می دهیم. به عدد 48 می رویم که از حاصل ضرب ضرایب اول آن 2 و 2 را می گیریم. سپس ضریب ساده 7 را از عدد چهارم و ضریب های 11 و 13 عدد پنجم را اضافه می کنیم. دریافت می کنیم: 2 2 2 2 3 7 11 13 = 48,048. این کمترین مضرب مشترک از پنج عدد اصلی است.

پاسخ: LCM (84، 6، 48، 7، 143) = 48،048.

یافتن کمترین مضرب مشترک اعداد منفی

برای یافتن کمترین مضرب مشترک اعداد منفی ابتدا باید این اعداد با اعدادی با علامت مخالف جایگزین شوند و سپس طبق الگوریتم های فوق محاسبات انجام شود.

مثال 9

LCM(54، -34) = LCM(54، 34) و LCM(-622، -46، -54، -888) = LCM(622، 46، 54، 888).

این گونه اعمال از این جهت جایز است که اگر پذیرفته شود آو - الف- اعداد مخالف
سپس مجموعه مضرب ها آبا مجموعه مضرب یک عدد منطبق است - الف.

مثال 10

محاسبه LCM اعداد منفی ضروری است − 145 و − 45 .

راه حل

بیایید اعداد را تغییر دهیم − 145 و − 45 به اعداد مخالف خود 145 و 45 . اکنون، با استفاده از الگوریتم، LCM (145، 45) = 145 45 را محاسبه می کنیم: GCD (145، 45) = 145 45: 5 = 1 305، که قبلاً GCD را با استفاده از الگوریتم اقلیدس تعیین کرده ایم.

دریافت می کنیم که LCM اعداد - 145 و − 45 برابر است 1 305 .

پاسخ: LCM (- 145، 45-) = 1 305.

اگر متوجه اشتباهی در متن شدید، لطفاً آن را برجسته کرده و Ctrl+Enter را فشار دهید