Lecture 3 General theorems of dynamics

Dynamics of the system of material points is an important branch of theoretical mechanics. Here, we mainly consider problems of the motion of mechanical systems (systems of material points) with a finite number of degrees of freedom - the maximum number of independent parameters that determine the position of the system. The main task of system dynamics is the study of the laws of motion of a rigid body and mechanical systems.

The simplest approach to studying the motion of a system, consisting of N material points, is reduced to the consideration of the movements of each individual point of the system. In this case, all forces acting on each point of the system, including the forces of interaction between points, must be determined.

Determining the acceleration of each point in accordance with Newton's second law (1.2), we obtain for each point three scalar differential laws of motion of the second order, i.e. 3 N differential law of motion for the entire system.

To find the equations of motion of a mechanical system for given forces and initial conditions for each point of the system, the obtained differential laws must be integrated. This problem is difficult even in the case of two material points that move only under the action of forces of interaction according to the law of universal attraction (the problem of two bodies), and is extremely difficult in the case of three interacting points (the problem of three bodies).

Therefore, it is necessary to find such methods for solving problems that would lead to solvable equations and give an idea of ​​the motion of a mechanical system. General theorems of dynamics, being a consequence of the differential laws of motion, make it possible to avoid the complexity that arises during integration and obtain the necessary results.

3.1. General remarks

The points of the mechanical system will be numbered by indices i, j, k etc. that run through all values 1, 2, 3… N, where N is the number of system points. Physical quantities related to k th point are denoted by the same index as the point. For example, they express respectively the radius vector and the speed k-th point.

Forces of two origin act on each of the points of the system: firstly, forces whose sources lie outside the system, called external forces and denoted by ; secondly, forces from other points of the given system, called internal forces and denoted by . Internal forces satisfy Newton's third law. Consider the simplest properties of internal forces acting on the entire mechanical system in any of its states.

First property. The geometric sum of all internal forces of the system (the main vector of internal forces) is equal to zero.

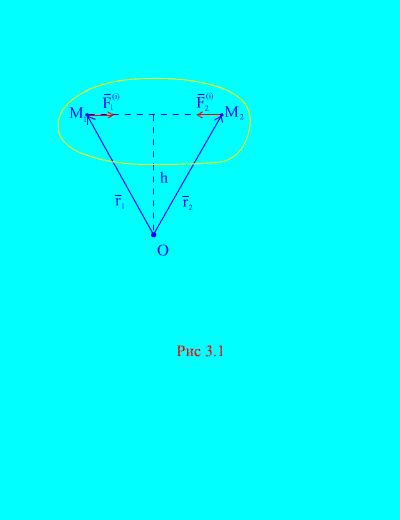
Indeed, if we consider any two arbitrary points of the system, for example, and (Fig. 3.1), then for them , because the forces of action and reaction are always equal in absolute value, they act along one line of action in the opposite direction, which connects the interacting points. The main vector of internal forces consists of pairs of forces of interacting points, therefore

(3.1)

Second property. The geometric sum of the moments of all internal forces relative to an arbitrary point in space is zero.

Consider the system of moments of forces and with respect to the point O(Fig. 3.1). From (Fig. 3.1). it's clear that

,

because both forces have the same arms and opposite directions of vector moments. The main moment of internal forces about the point O consists of the vector sum of such expressions and is equal to zero. Consequently,

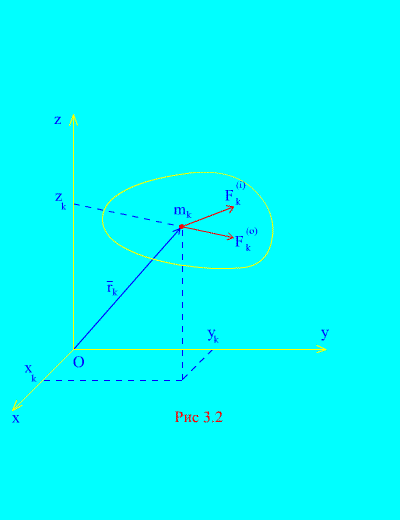
Let external and internal forces acting on a mechanical system consisting of N points (Fig. 3.2). If the resultant of external forces and the resultant of all internal forces are applied to each point of the system, then for any k th point of the system, one can compose differential equations of motion. In total such equations will be N:

and in projections onto fixed coordinate axes 3 N:

(3.4)

Vector equations (3.3) or equivalent scalar equations (3.4) represent the differential laws of motion of material points of the entire system. If all points move parallel to one plane or one straight line, then the number of equations (3.4) in the first case will be 2 N, in the second N.

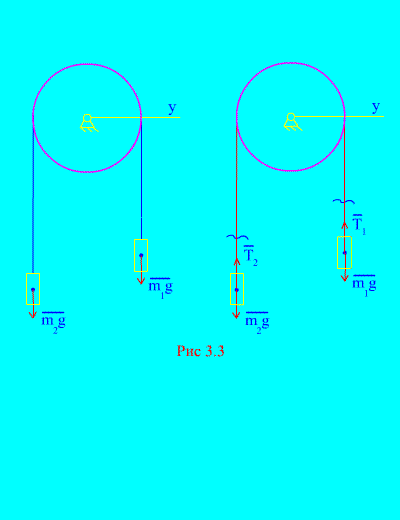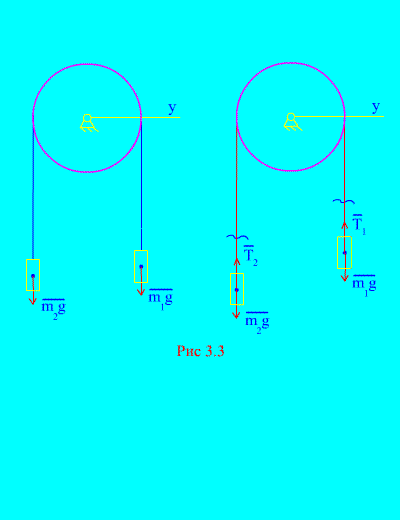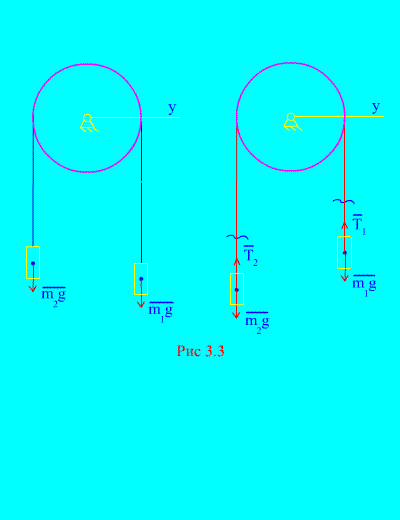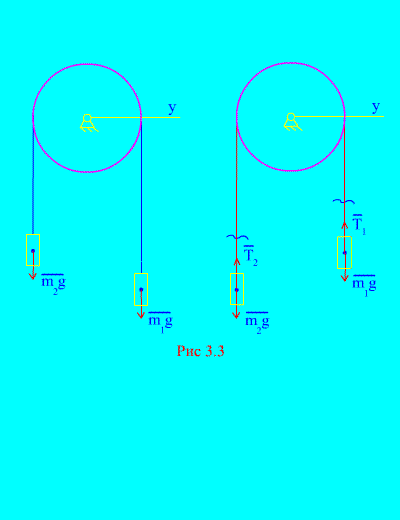
Example 1 Two loads of mass and are interconnected by an inextensible cable thrown over a block (Fig. 3.3). Neglecting the forces of friction, as well as the mass of the block and the cable, determine the law of movement of goods and the tension of the cable.

Solution. The system consists of two material bodies (connected by an inextensible cable) moving parallel to one axis X. Let us write down the differential laws of motion in projections onto the axis X for every body.

Let the right weight descend with acceleration , then the left weight will rise with acceleration . We mentally free ourselves from the connection (cable) and replace it with reactions and (Fig. 3.3). Considering the bodies to be free, we will compose the differential laws of motion in the projection onto the axis X(meaning that the thread tensions are internal forces, and the weight of the loads are external):

Since and (the bodies are connected by an inextensible cable), we obtain

Solving these equations for the acceleration and tension of the cable T, we get

.

Note that the cable tension at is not equal to the gravity of the corresponding load.

3. 2. The theorem on the motion of the center of mass

It is known that a rigid body and a mechanical system in a plane can move quite difficult. The first theorem on the motion of a body and a mechanical system can be arrived at in the following way: drop the c.-l. an object consisting of many solid bodies fastened together. It is clear that he will fly in a parabola. This was revealed when studying the motion of a point. However, now the object is not a point. It turns, sways in the process of flying around some effective center, which moves along a parabola. The first theorem on the motion of complex objects says that a certain effective center is the center of mass of a moving object. The center of mass is not necessarily located in the body itself, it can lie somewhere outside it.

Theorem. The center of mass of a mechanical system moves as a material point with a mass equal to the mass of the entire system, to which all external forces acting on the system are applied.

To prove the theorem, we rewrite the differential laws of motion (3.3) in the following form:

(3.5)

where N is the number of system points.

Let's add the equations together term by term:

(a)

The position of the center of mass of the mechanical system relative to the selected coordinate system is determined by formula (2.1): where M is the mass of the system. Then the left side of equality (a) is written

The first sum, standing on the right side of equality (a), is equal to the main vector of external forces, and the last one, by the property of internal forces, is equal to zero. Then equality (a), taking into account (b), will be rewritten

, (3.6)

those. the product of the mass of the system and the acceleration of the center of its mass is equal to the geometric sum of all external forces acting on the system.

It follows from equation (3.6) that internal forces do not directly affect the motion of the center of mass. However, in some cases they are the cause of the appearance of external forces applied to the system. Thus, the internal forces that rotate the driving wheels of the car cause the action on it of an external adhesion force applied to the wheel rim.

Example 2 The mechanism, located in a vertical plane, is installed on a horizontal smooth plane and attached to it with bars rigidly fixed to the surface. To and L (Fig. 3.4).

Disc 1 radius R motionless. Disc 2 mass m and radius r fastened with a crank, length R+ r at the point From 2. The crank rotates at a constant

angular speed. At the initial moment, the crank occupied the right horizontal position. Neglecting the mass of the crank, determine the maximum horizontal and vertical forces acting on the bars, if the total mass of the frame and wheel 1 is equal to M. Also consider the behavior of the mechanism in the absence of bars.

Solution. The system consists of two masses ( N=2 ): a fixed disk 1 with a frame and a movable disk 2. Let's direct the axis at through the center of gravity of the fixed disk vertically upwards, the axis X- along the horizontal plane.

We write the theorem on the motion of the center of mass (3.6) in the coordinate form

The external forces of this system are: the weight of the frame and the fixed disk - mg, movable disc weight mg, - the total horizontal reaction of the bolts, - the normal total reaction of the plane. Consequently,

Then the laws of motion (b) are rewritten

Let us calculate the coordinates of the center of mass of the mechanical system:

; (G)

as seen from (Fig. 3.4), , , (angle of rotation of the crank), . Substituting these expressions in (r) and calculating the second derivatives with respect to time t from , , we get that

(e)

Substituting (c) and (e) into (b), we find

The horizontal pressure acting on the bars is greatest and least when cos = 1 respectively, i.e.

The pressure of the mechanism on the horizontal plane has the highest and lowest values ​​when sin respectively, i.e.

In fact, the first problem of dynamics has been solved: according to the known equations of motion of the center of mass of the system (e), the forces involved in the motion are restored.

In the absence of bars K and L (Fig. 3.4), the mechanism may begin to bounce above the horizontal plane. This will take place when , i.e. when , it follows that the angular velocity of rotation of the crank, at which the mechanism bounces, must satisfy the equality

.

3. 3. Law of conservation of motion of the center of mass

If the main vector of external forces acting on the system is equal to zero, i.e. , then from(3.6)it follows that the acceleration of the center of mass is zero, therefore, the velocity of the center of mass is constant in magnitude and direction. If, in particular, at the initial moment the center of mass is at rest, then it is at rest for the entire time while the main vector of external forces is equal to zero.

Several corollaries follow from this theorem.

· Internal forces alone cannot change the nature of the movement of the center of mass of the system.

· If the main vector of external forces acting on the system is equal to zero, then the center of mass is at rest or moves uniformly and rectilinearly.

· If the projection of the main vector of the external forces of the system on some fixed axis is equal to zero, then the projection of the velocity of the center of mass of the system on this axis does not change.

· A pair of forces applied to a rigid body cannot change the motion of its center of mass (it can only cause the body to rotate around the center of mass).

Let's consider an example illustrating the law of conservation of motion of the center of mass.

Example 3 Two weights with masses and are connected by an inextensible thread thrown over a block (Fig. 3.5), fixed on a wedge with mass M. The wedge rests on a smooth horizontal plane. Initially, the system was at rest. Find the displacement of the wedge along the plane when the first load is lowered to a height N. Ignore the mass of the block and the thread.

Solution. The external forces acting on the wedge together with the weights are the forces of gravity , and mg, as well as the normal response of a smooth horizontal surface N. Therefore,

Since the system was at rest at the initial moment, we have .

Let us calculate the coordinate of the center of mass of the system at and at the moment t 1 when the weight of the load g descend to a height H.

For a moment:

,

where , , X- respectively, the coordinates of the center of mass of loads weighing g, g and wedge weighing Mg.

Let us assume that the wedge at the moment of time moves in the positive direction of the axis Ox by the amount L if the weight of the load falls to a height N. Then, for a moment

because loads together with the wedge will move to L to the right, a the weight will move a distance up the wedge. Since , after calculations we get

.

3.4. Quantity of movement system

3.4.1. Computing the momentum of a system

The momentum of a material point is a vector quantity equal to the product of the mass of the point and the vector of its velocity

Unit of measurement of the amount of movement -

The momentum of a mechanical system is called the vector sum of the momentum of the individual points of the system, i.e.

where N is the number of system points.

The momentum of a mechanical system can be expressed in terms of the mass of the system M and the speed of the center of mass. Really,

those. the momentum of the system is equal to the product of the mass of the entire system and the velocity of its center of mass. The direction is the same as the direction (Fig. 3.6)

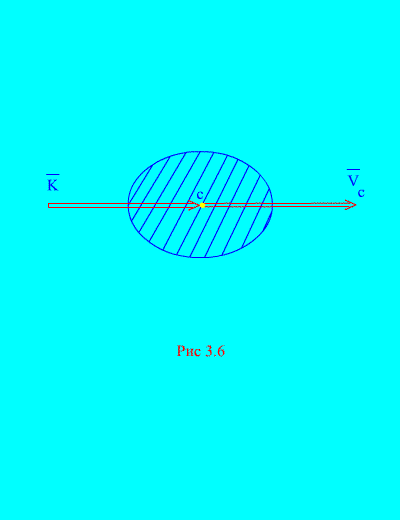
In projections onto rectangular axes, we have

where , , - projections of the velocity of the center of mass of the system.

Here M is the mass of the mechanical system; does not change as the system moves.

It is especially convenient to use these results when calculating the momenta of rigid bodies.

It can be seen from formula (3.7) that if a mechanical system moves in such a way that its center of mass remains stationary, then the momentum of the system remains equal to zero.

3.4.2. Elemental and full force impulse

The action of a force on a material point over time dt can be characterized by an elementary impulse. Total impulse of force in time t, or momentum of force, is determined by the formula

or in projections onto the coordinates of the axis

(3.8a)

The unit of force impulse is .

3.4.3. Theorem on the change in the momentum of the system

Let external and internal forces be applied to the points of the system. Then, for each point of the system, we can apply the differential laws of motion (3.3), bearing in mind that :

.

Summing over all points of the system, we obtain

By the property of internal forces and by definition we have

(3.9)

Multiplying both sides of this equation by dt, we obtain the theorem on the change in the momentum in differential form:

, (3.10)

those. the differential of the momentum of a mechanical system is equal to the vector sum of the elementary impulses of all external forces acting on the points of the mechanical system.

Calculating the integral of both parts of (3.10) over time from 0 to t, we obtain the theorem in finite or integral form

(3.11)

In projections onto the coordinate axes, we will have

Change in momentum of a mechanical system over timet, is equal to the vector sum of all impulses of external forces acting on the points of the mechanical system in the same time.

Example 4 Load of mass m descends down an inclined plane from rest under the action of a force F, proportional to time: , where (Fig. 3.7). What is the speed of the body after t seconds after the start of movement, if the coefficient of sliding friction of the load on the inclined plane is equal to f.

Solution. Let's depict the forces applied to the load: mg - gravity of the load, N is the normal reaction of the plane, is the sliding friction force of the load on the plane, and . The direction of all forces is shown in (Fig. 3.7).

Let's direct the axis X down an inclined plane. Let us write the theorem on the change in momentum (3.11) in the projection onto the axis X:

(a)

By condition, because at the initial moment of time, the load was at rest. The sum of the projections of the impulses of all forces on the x-axis is

Consequently,

,

.

3.4.4. Laws of conservation of momentum

Conservation laws are obtained as special cases of the momentum change theorem. There are two special cases.

· If the vector sum of all external forces applied to the system is equal to zero, i.e. , then it follows from the theorem (3.9) , what ,

those. if the main vector of external forces of the system is equal to zero, then the momentum of the system is constant in magnitude and direction.

· If the projection of the main vector of external forces on any coordinate axis is equal to zero, for example, Ox, i.e. , then the projection of the amount of motion on this axis is constant.

Consider an example of applying the law of conservation of momentum.

Example 5 A ballistic pendulum is a body of mass , suspended on a long string (Fig. 3.8).

A bullet of mass moving at a speed V and falling into a motionless body, gets stuck in it, and the body is deflected. What was the speed of the bullet if the body rose to a height h ?

Solution. Let the body with the stuck bullet acquire speed . Then, using the law of conservation of momentum in the interaction of two bodies, we can write .

Velocity can be calculated using the law of conservation of mechanical energy . Then . As a result, we find

.

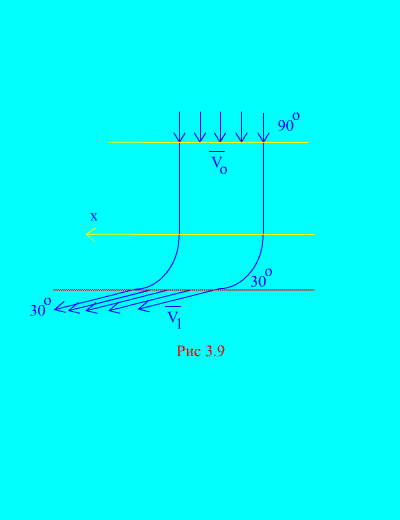
Example 6. Water enters a fixed channel (Fig. 3.9) variable section with a speed at an angle to the horizon; cross-sectional area of ​​the channel at the entrance; the speed of the water at the outlet of the channel and makes an angle with the horizon.

Determine the horizontal component of the reaction that water exerts on the walls of the channel. Density of water .

Solution. We will determine the horizontal component of the reaction exerted by the channel walls on water. This force is equal in absolute value and opposite in sign to the desired force. We have, according to (3.11a),

. (a)

We calculate the mass of the volume of liquid entering the channel during the time t:

The value of rAV 0 is called second mass - the mass of liquid flowing through any section of the pipe per unit time.

The same amount of water leaves the canal in the same time. The initial and final speeds are given in the condition.

Let us calculate the right side of equality (a) which determines the sum of projections onto the horizontal axis of external forces applied to the system (water). The only horizontal force is the horizontal component of the resultant reaction of the walls R x. This force is constant during the steady motion of water. That's why

. (in)

Substituting (b) and (c) into (a), we get

3.5. The momentum of the system

3.5.1. Principal moment of momentum of the system

Let be the radius vector of a point with the mass of the system relative to some point A, called the center (Fig. 3.10).

Moment of momentum (kinetic moment) of a point relative to the center A called vector , determined by the formula

. (3.12)

In this case, the vector directed perpendicular to the plane passing through the center BUT and vector .

Moment of momentum (kinetic moment) of a point about an axis is called the projection onto this axis of the angular momentum of the point relative to any center chosen on this axis.

The main moment of momentum (kinetic moment) of the system relative to the center A is called the quantity

(3.13)

The main moment of momentum (kinetic moment) of the system about the axis is called the projection onto this axis of the main moment of the momentum of the system relative to any chosen on the given center axis.

3.5.2. Momentum of a rotating rigid body about the axis of rotation

Compatible fixed point O body lying on the axis of rotation Oz, with the origin of the coordinate system Ohuz, whose axes will rotate with the body (Fig. 3.11). Let be the radius vector of the point of the body relative to the origin of coordinates, its projections on the axes will be denoted by , , . The projections of the angular velocity vector of the body on the same axes will be denoted by 0, 0, ().

Consider the motion of a certain system of material volumes relative to a fixed coordinate system. When the system is not free, then it can be considered as free, if we discard the constraints imposed on the system and replace their action with the corresponding reactions.

Let us divide all the forces applied to the system into external and internal ones; both may include reactions of discarded

connections. Denote by and the main vector and the main moment of external forces relative to point A.

1. Theorem on the change in momentum. If is the momentum of the system, then (see )

i.e., the theorem is valid: the time derivative of the momentum of the system is equal to the main vector of all external forces.

Replacing the vector through its expression where is the mass of the system, is the velocity of the center of mass, equation (4.1) can be given a different form:

This equality means that the center of mass of the system moves as a material point whose mass is equal to the mass of the system and to which a force is applied that is geometrically equal to the main vector of all external forces of the system. The last statement is called the theorem on the motion of the center of mass (center of inertia) of the system.

If then from (4.1) it follows that the momentum vector is constant in magnitude and direction. Projecting it on the coordinate axis, we obtain three scalar first integrals of the differential equations of the system's double chain:

These integrals are called momentum integrals. When the speed of the center of mass is constant, i.e., it moves uniformly and rectilinearly.

If the projection of the main vector of external forces on any one axis, for example, on the axis, is equal to zero, then we have one first integral, or if two projections of the main vector are equal to zero, then there are two integrals of the momentum.

2. Theorem on the change of the kinetic moment. Let A be some arbitrary point in space (moving or stationary), which does not necessarily coincide with any particular material point of the system during the entire time of movement. We denote its velocity in a fixed system of coordinates by The theorem on the change in the angular momentum of a material system relative to point A has the form

If point A is fixed, then equality (4.3) takes a simpler form:

This equality expresses the theorem on the change of the angular momentum of the system relative to a fixed point: the time derivative of the angular momentum of the system, calculated relative to some fixed point, is equal to the main moment of all external forces relative to this point.

If then, according to (4.4), the angular momentum vector is constant in magnitude and direction. Projecting it on the coordinate axis, we obtain the scalar first integrals of the differential equations of the motion of the system:

These integrals are called integrals of angular momentum or area integrals.

If point A coincides with the center of mass of the system, Then the first term on the right side of equality (4.3) vanishes and the theorem on the change in angular momentum has the same form (4.4) as in the case of a fixed point A. Note (see 4 § 3) that in the case under consideration the absolute angular momentum of the system on the left side of equality (4.4) can be replaced by the equal angular momentum of the system in its motion relative to the center of mass.

Let be some constant axis or an axis of constant direction passing through the center of mass of the system, and let be the angular momentum of the system relative to this axis. From (4.4) it follows that

where is the moment of external forces about the axis. If during the whole time of motion then we have the first integral

In the works of S. A. Chaplygin, several generalizations of the theorem on the change in angular momentum were obtained, which were then applied in solving a number of problems on the rolling of balls. Further generalizations of the theorem on the change of the kpnetological moment and their applications in problems of the dynamics of a rigid body are contained in the works. The main results of these works are related to the theorem on the change in the angular momentum relative to the moving one, constantly passing through some moving point A. Let be a unit vector directed along this axis. Multiplying scalarly by both sides of equality (4.3) and adding the term to both its parts, we obtain

When the kinematic condition is met

equation (4.5) follows from (4.7). And if condition (4.8) is satisfied during the whole time of motion, then the first integral (4.6) exists.

If the connections of the system are ideal and allow rotation of the system as a rigid body around the axis and in the number of virtual displacements, then the main moment of reactions about the axis and is equal to zero, and then the value on the right side of equation (4.5) is the main moment of all external active forces about the axis and . The equality to zero of this moment and the satisfiability of relation (4.8) will be in the case under consideration sufficient conditions for the existence of the integral (4.6).

If the direction of the axis and is unchanged, then condition (4.8) can be written as

This equality means that the projections of the velocity of the center of mass and the velocity of point A on the axis and on the plane perpendicular to this are parallel. In the work of S. A. Chaplygin, instead of (4.9), a less general condition is required where X is an arbitrary constant.

Note that condition (4.8) does not depend on the choice of a point on . Indeed, let P be an arbitrary point on the axis. Then

and hence

In conclusion, we note the geometric interpretation of Resal's equations (4.1) and (4.4): the vectors of the absolute velocities of the ends of the vectors and are equal, respectively, to the main vector and the main moment of all external forces relative to the point A.

Ministry of Education and Science of the Russian Federation

Federal State Budgetary Educational Institution of Higher Professional Education

"Kuban State Technological University"

Theoretical mechanics

Part 2 dynamics

Approved by the Editorial and Publishing

university council as

study guide

Krasnodar

UDC 531.1/3 (075)

Theoretical mechanics. Part 2. Dynamics: Textbook / L.I.Draiko; Kuban. state. technol.un-t. Krasnodar, 2011. 123 p.

ISBN 5-230-06865-5

The theoretical material is presented in a brief form, examples of problem solving are given, most of which reflect real technical issues, attention is paid to the choice of a rational solution method.

Designed for bachelors of correspondence and distance learning in construction, transport and engineering areas.

Tab. 1 Fig. 68 Bibliography. 20 titles

Scientific editor Candidate of Technical Sciences, Assoc. V.F. Melnikov

Reviewers: Head of the Department of Theoretical Mechanics and Theory of Mechanisms and Machines of the Kuban Agrarian University prof. F.M. Kanarev; Associate Professor of the Department of Theoretical Mechanics of the Kuban State Technological University M.E. Multykh

Published by decision of the Editorial and Publishing Council of the Kuban State Technological University.

Reissue

ISBN 5-230-06865-5 KubGTU 1998

Foreword

This textbook is intended for part-time students of construction, transport and engineering specialties, but can be used when studying the section "Dynamics" of the course of theoretical mechanics by part-time students of other specialties, as well as full-time students with independent work.

The manual is compiled in accordance with the current program of the course of theoretical mechanics, covers all issues of the main part of the course. Each section contains a brief theoretical material, provided with illustrations and guidelines for its use in solving problems. The manual analyzes the solution of 30 problems, reflecting the real issues of technology and the corresponding control tasks for independent solution. For each task, a calculation scheme is presented that clearly illustrates the solution. The design of the solution complies with the requirements for the design of examinations of part-time students.

The author expresses his deep gratitude to the teachers of the Department of Theoretical Mechanics and Theory of Mechanisms and Machines of the Kuban Agrarian University for their great work in reviewing the textbook, as well as to the teachers of the Department of Theoretical Mechanics of the Kuban State Technological University for valuable comments and advice on preparing the textbook for publication.

All critical comments and wishes will be accepted by the author with gratitude in the future.

Introduction

Dynamics is the most important branch of theoretical mechanics. Most of the specific tasks that occur in engineering practice relate to dynamics. Using the conclusions of statics and kinematics, dynamics establishes the general laws of motion of material bodies under the action of applied forces.

The simplest material object is a material point. For a material point, one can take a material body of any shape, the dimensions of which in the problem under consideration can be neglected. A body of finite dimensions can be taken as a material point if the difference in the motion of its points is not significant for a given problem. This happens when the dimensions of the body are small compared to the distances that the points of the body pass. Each particle of a solid body can be considered a material point.

The forces applied to a point or a material body are evaluated in dynamics by their dynamic impact, i.e., by how they change the characteristics of the movement of material objects.

The movement of material objects over time takes place in space relative to a certain frame of reference. In classical mechanics, based on Newton's axioms, space is considered three-dimensional, its properties do not depend on material objects moving in it. The position of a point in such space is determined by three coordinates. Time is not connected with space and movement of material objects. It is considered the same for all reference systems.

The laws of dynamics describe the movement of material objects in relation to the absolute coordinate axes, conventionally taken as immovable. The origin of the absolute coordinate system is taken at the center of the Sun, and the axes are directed to distant, conditionally stationary stars. When solving many technical problems, coordinate axes associated with the Earth can be considered conditionally immovable.

The parameters of the mechanical motion of material objects in dynamics are established by mathematical deductions from the basic laws of classical mechanics.

First law (law of inertia):

A material point maintains a state of rest or uniform and rectilinear motion until the action of any forces takes it out of this state.

Uniform and rectilinear motion of a point is called motion by inertia. Rest is a special case of motion by inertia, when the speed of a point is zero.

Any material point has inertia, i.e., it tends to maintain a state of rest or uniform rectilinear motion. The frame of reference, in relation to which the law of inertia is satisfied, is called inertial, and the motion observed in relation to this frame is called absolute. Any frame of reference that performs translational rectilinear and uniform motion relative to the inertial frame will also be an inertial frame.

The second law (basic law of dynamics):

The acceleration of a material point relative to the inertial frame of reference is proportional to the force applied to the point and coincides with the force in the direction:
.

It follows from the basic law of dynamics that with a force
acceleration
. The mass of a point characterizes the degree of resistance of a point to a change in its speed, that is, it is a measure of the inertia of a material point.

Third law (law of action and reaction):

The forces with which two bodies act on each other are equal in magnitude and directed along one straight line in opposite directions.

The forces called action and reaction are applied to different bodies and therefore do not form a balanced system.

The fourth law (the law of the independence of the action of forces):

With the simultaneous action of several forces, the acceleration of a material point is equal to the geometric sum of the accelerations that the point would have under the action of each force separately:

, where
,
,…,
.

Quite often, it is possible to isolate important features of the motion of a mechanical system without resorting to integrating the system of differential equations of motion. This is achieved by applying general theorems of dynamics.

5.1. Basic concepts and definitions

External and internal forces. Any force acting on a point of a mechanical system is necessarily either an active force or a coupling reaction. The entire set of forces acting on the points of the system can be divided into two classes differently: into external forces and internal forces (indices e and i - from the Latin words externus - external and internus - internal). External forces are called forces acting on points of the system from points and bodies that are not part of the system under consideration. Forces of interaction between points and bodies of the considered system are called internal.

This division depends on what material points and bodies are included by the researcher in the considered mechanical system. If the composition of the system is expanded to include additional points and bodies, then some forces that were external for the previous system may become internal for the expanded system.

Properties of internal forces. Since these forces are forces of interaction between parts of the system, they are included in the complete system of internal forces in "twos" organized in accordance with the action-reaction axiom. Each such "two" of forces

the main vector and the main moment about an arbitrary center are equal to zero. Since the complete system of internal forces consists only of "twos", then

1) the main vector of the system of internal forces is equal to zero,

2) the main moment of the system of internal forces relative to an arbitrary point is equal to zero.

The mass of the system is the arithmetic sum of the masses mk of all points and bodies that form the system:

center of gravity(center of inertia) of a mechanical system is a geometric point C, the radius vector and coordinates of which are determined by the formulas

where are the radius vectors and the coordinates of the points that form the system.

For a rigid body in a uniform gravitational field, the positions of the center of mass and the center of gravity coincide; in other cases, these are different geometric points.

Together with the inertial frame of reference, one often considers simultaneously a non-inertial frame of reference moving forward. Its coordinate axes (Koenig axes) are chosen so that the reference point C always coincides with the center of mass of the mechanical system. In accordance with the definition, the center of mass is fixed in the Koenig axes and is located at the origin of coordinates.

The moment of inertia of the system relative to the axis is called a scalar quantity equal to the sum of the products of the masses mk of all points of the system by the squares of their distances to the axis:

If the mechanical system is a rigid body, to find 12, you can use the formula

where is the density, the volume occupied by the body.