Tangent to a function at a point. online calculator

The article gives a detailed explanation of the definitions, the geometric meaning of the derivative with graphic notation. The equation of the tangent line will be considered with examples, the equations of the tangent to curves of the 2nd order will be found.

Yandex.RTB R-A-339285-1 Definition 1

The angle of inclination of the straight line y \u003d k x + b is called the angle α, which is measured from the positive direction of the x-axis to the straight line y \u003d k x + b in the positive direction.

In the figure, the direction ox is indicated by a green arrow and a green arc, and the angle of inclination by a red arc. The blue line refers to a straight line.

Definition 2

The slope of the straight line y \u003d k x + b is called the numerical coefficient k.

The slope is equal to the slope of the straight line, in other words k = t g α .

• The slope of the straight line is 0 only when o x is parallel and the slope equals zero, because the tangent of zero is 0. So, the form of the equation will be y = b.
• If the angle of inclination of the straight line y = k x + b is acute, then the conditions 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 , and there is an increase in the graph.
• If α \u003d π 2, then the location of the line is perpendicular to x. Equality is specified by the equality x = c with the value c being a real number.
• If the angle of inclination of the straight line y = k x + b is obtuse, then it corresponds to the conditions π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definition 3

A secant is a straight line that passes through 2 points of the function f (x). In other words, a secant is a straight line that passes through any two points on the graph of a given function.

The figure shows that A B is a secant, and f (x) is a black curve, α is a red arc, indicating the angle of inclination of the secant.

When the slope of a straight line is equal to the tangent of the angle of inclination, it is clear that the tangent from a right triangle A B C can be found in relation to the opposite leg to the adjacent one.

Definition 4

We get the formula for finding the secant of the form:

k = t g α = B C A C = f (x B) - f x A x B - x A , where the abscissas of points A and B are the values ​​x A , x B , and f (x A) , f (x B) are the values functions at these points.

Obviously, the slope of the secant is defined using the equality k \u003d f (x B) - f (x A) x B - x A or k \u003d f (x A) - f (x B) x A - x B, and the equation must be written as y = f (x B) - f (x A) x B - x A x - x A + f (x A) or
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

The secant visually divides the graph into 3 parts: to the left of point A, from A to B, to the right of B. The figure below shows that there are three secants that are considered to be the same, that is, they are set using a similar equation.

By definition, it is clear that the line and its secant coincide in this case.

A secant can intersect the graph of a given function multiple times. If there is an equation of the form y \u003d 0 for the secant, then the number of intersection points with the sinusoid is infinite.

Definition 5

Tangent to the graph of the function f (x) at the point x 0 ; f (x 0) is called a straight line passing through a given point x 0; f (x 0) , with the presence of a segment that has many x values ​​close to x 0 .

Example 1

Let's take a closer look at the example below. Then it can be seen that the line given by the function y = x + 1 is considered to be tangent to y = 2 x at the point with coordinates (1 ; 2) . For clarity, it is necessary to consider graphs with values ​​close to (1; 2). The function y = 2 x is marked in black, the blue line is the tangent, the red dot is the point of intersection.

Obviously, y \u003d 2 x merges with the line y \u003d x + 1.

To determine the tangent, consider the behavior of the tangent A B as point B approaches point A infinitely. For clarity, we present a figure.

The secant A B, indicated by the blue line, tends to the position of the tangent itself, and the angle of inclination of the secant α will begin to tend to the angle of inclination of the tangent itself α x.

Definition 6

The tangent to the graph of the function y \u003d f (x) at point A is the limiting position of the secant A B at B tending to A, that is, B → A.

Now we turn to the consideration of the geometric meaning of the derivative of a function at a point.

Let's move on to the consideration of the secant A B for the function f (x), where A and B with coordinates x 0, f (x 0) and x 0 + ∆ x, f (x 0 + ∆ x), and ∆ x is denoted as an increment of the argument . Now the function will take the form ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . For clarity, let's take a picture as an example.

Consider the resulting right triangle A B C. We use the definition of the tangent for the solution, that is, we obtain the ratio ∆ y ∆ x = t g α . It follows from the definition of a tangent that lim ∆ x → 0 ∆ y ∆ x = t g α x . According to the derivative rule at a point, we have that the derivative f (x) at the point x 0 is called the limit of the ratio of the increment of the function to the increment of the argument, where ∆ x → 0, then denoted as f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

It follows that f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, where k x is denoted as the slope of the tangent.

That is, we obtain that f ' (x) can exist at the point x 0 and, as well as the tangent to the given graph of the function at the point of contact equal to x 0 , f 0 (x 0) , where the value of the slope of the tangent at the point is equal to the derivative at the point x 0 . Then we get that k x = f "(x 0) .

The geometric meaning of the derivative of a function at a point is that the concept of the existence of a tangent to the graph at the same point is given.

To write the equation of any straight line in the plane, it is necessary to have a slope with the point through which it passes. Its designation is taken as x 0 at the intersection.

The equation of the tangent to the graph of the function y \u003d f (x) at the point x 0, f 0 (x 0) takes the form y \u003d f "(x 0) x - x 0 + f (x 0) .

It means that the final value of the derivative f "(x 0) can determine the position of the tangent, that is, vertically under the condition lim x → x 0 + 0 f" (x) = ∞ and lim x → x 0 - 0 f "(x ) = ∞ or absence at all under the condition lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) .

The location of the tangent depends on the value of its slope k x \u003d f "(x 0). When parallel to the x axis, we get that k k \u003d 0, when parallel to about y - k x \u003d ∞, and the form of the tangent equation x \u003d x 0 increases with k x > 0 , decreases as k x< 0 .

Example 2

Compile the equation of the tangent to the graph of the function y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 at a point with coordinates (1; 3) with the definition of the angle of inclination.

Solution

By assumption, we have that the function is defined for all real numbers. We get that the point with the coordinates specified by the condition (1 ; 3) is the point of contact, then x 0 = - 1 , f (x 0) = - 3 .

It is necessary to find the derivative at the point with value - 1 . We get that

y "= e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" = = e x + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = e x + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

The value of f ’ (x) at the point of contact is the slope of the tangent, which is equal to the tangent of the slope.

Then k x = t g α x = y "(x 0) = 3 3

It follows that α x = a r c t g 3 3 = π 6

Answer: the tangent equation takes the form

y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

For clarity, we give an example in a graphic illustration.

Black color is used for the graph of the original function, blue color is the tangent image, red dot is the touch point. The figure on the right shows an enlarged view.

Example 3

Find out the existence of a tangent to the graph of a given function
y = 3 x - 1 5 + 1 at the point with coordinates (1 ; 1) . Write an equation and determine the angle of inclination.

Solution

By assumption, we have that the domain of the given function is the set of all real numbers.

Let's move on to finding the derivative

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

If x 0 = 1 , then f ' (x) is not defined, but the limits are written as lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ and lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , which means existence vertical tangent at point (1 ; 1) .

Answer: the equation will take the form x \u003d 1, where the angle of inclination will be equal to π 2.

Let's graph it for clarity.

Example 4

Find the points of the function graph y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , where

1. The tangent does not exist;
2. The tangent is parallel to x;
3. The tangent is parallel to the line y = 8 5 x + 4 .

Solution

It is necessary to pay attention to the domain of definition. By assumption, we have that the function is defined on the set of all real numbers. Expand the module and solve the system with intervals x ∈ - ∞ ; 2 and [ - 2 ; +∞) . We get that

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

The function needs to be differentiated. We have that

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

When x = - 2, then the derivative does not exist because the one-sided limits are not equal at that point:

lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

We calculate the value of the function at the point x \u003d - 2, where we get that

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, that is, the tangent at the point (- 2; - 2) will not exist.
2. The tangent is parallel to x when the slope is zero. Then k x \u003d t g α x \u003d f "(x 0). That is, it is necessary to find the values ​​\u200b\u200bof such x when the derivative of the function turns it to zero. That is, the values ​​\u200b\u200bof f '(x) and will be the touch points, where the tangent is parallel about x .

When x ∈ - ∞ ; - 2 , then - 1 5 (x 2 + 12 x + 35) = 0 , and for x ∈ (- 2 ; + ∞) we get 1 5 (x 2 - 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

We calculate the corresponding values ​​of the function

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Hence - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 are considered to be the desired points of the graph of the function.

Consider a graphical representation of the solution.

The black line is the graph of the function, the red dots are the touch points.

1. When the lines are parallel, the slopes are equal. Then it is necessary to search for the points of the graph of the function, where the slope will be equal to the value 8 5 . To do this, you need to solve an equation of the form y "(x) = 8 5. Then, if x ∈ - ∞; - 2, we get that - 1 5 (x 2 + 12 x + 35) = 8 5, and if x ∈ ( - 2 ; + ∞) , then 1 5 (x 2 - 4 x + 3) = 8 5 .

The first equation has no roots because the discriminant is less than zero. Let's write down that

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Another equation has two real roots, then

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Let's move on to finding the values ​​of the function. We get that

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Points with values ​​- 1 ; 4 15 , 5 ; 8 3 are the points where the tangents are parallel to the line y = 8 5 x + 4 .

Answer: black line - graph of the function, red line - graph y \u003d 8 5 x + 4, blue line - tangents at points - 1; 4 15 , 5 ; 8 3 .

The existence of an infinite number of tangents for given functions is possible.

Example 5

Write the equations of all available tangents of the function y = 3 cos 3 2 x - π 4 - 1 3 , which are perpendicular to the line y = - 2 x + 1 2 .

Solution

To draw up the tangent equation, it is necessary to find the coefficient and coordinates of the point of contact, based on the condition of perpendicularity of the lines. The definition sounds like this: the product of the slopes that are perpendicular to the straight lines is equal to - 1, that is, it is written as k x · k ⊥ = - 1. From the condition we have that the slope is perpendicular to the straight line and equals k ⊥ = - 2, then k x = - 1 k ⊥ = - 1 - 2 = 1 2 .

Now we need to find the coordinates of the touch points. You need to find x, after which its value for a given function. Note that from the geometric meaning of the derivative at the point
x 0 we get that k x \u003d y "(x 0) . From this equality, we find the x values ​​\u200b\u200bfor the touch points.

We get that

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ k x \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

This trigonometric equation will be used to calculate the ordinates of the touch points.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk or 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk or 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk or x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z is the set of integers.

Found x points of contact. Now you need to go to the search for y values:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 or y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 or y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 or y 0 = - 4 5 + 1 3

From here we get that 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 are touch points.

Answer: the necessary equations will be written as

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

For a visual representation, consider the function and the tangent on the coordinate line.

The figure shows that the location of the function is on the interval [ - 10 ; 10 ] , where the black line is the graph of the function, the blue lines are tangents that are perpendicular to the given line of the form y = - 2 x + 1 2 . Red dots are touch points.

The canonical equations of curves of the 2nd order are not single-valued functions. Tangent equations for them are compiled according to well-known schemes.

Tangent to circle

To set a circle centered at a point x c e n t e r ; y c e n t e r and radius R, the formula x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 is used.

This equality can be written as the union of two functions:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

The first function is at the top and the second at the bottom, as shown in the figure.

To draw up an equation of a circle at a point x 0 ; y 0 , which is located in the upper or lower semicircle, you should find the equation of the function graph of the form y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r or y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e r at the specified point.

When at points x c e n t e r ; y c e n t e r + R and x c e n t e r ; y c e n t e r - R tangents can be given by the equations y = y c e n t e r + R and y = y c e n t e r - R , and at points x c e n t e r + R ; y c e n t e r and
x c e n t e r - R ; y c e n t e r will be parallel about y, then we will get equations of the form x = x c e n t e r + R and x = x c e n t e r - R .

Tangent to Ellipse

When the ellipse is centered at x c e n t e r ; y c e n t e r with semiaxes a and b , then it can be given using the equation x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .

An ellipse and a circle can be denoted by combining two functions, namely, the upper and lower semi-ellipse. Then we get that

y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

If the tangents are located at the vertices of the ellipse, then they are parallel about x or about y. For clarity, consider the figure below.

Example 6

Write the equation of the tangent to the ellipse x - 3 2 4 + y - 5 2 25 = 1 at points with x values ​​equal to x = 2 .

Solution

It is necessary to find touch points that correspond to the value x = 2. We make a substitution into the existing equation of the ellipse and obtain that

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Then 2 ; 5 3 2 + 5 and 2 ; - 5 3 2 + 5 are the tangent points that belong to the upper and lower semi-ellipse.

Let's move on to finding and resolving the equation of an ellipse with respect to y. We get that

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

It is obvious that the upper semi-ellipse is specified using a function of the form y = 5 + 5 2 4 - x - 3 2 , and the lower one y = 5 - 5 2 4 - x - 3 2 .

We apply the standard algorithm in order to formulate the equation of the tangent to the graph of a function at a point. We write that the equation for the first tangent at point 2 ; 5 3 2 + 5 will look like

y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

We get that the equation of the second tangent with the value at the point
2; - 5 3 2 + 5 becomes

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graphically, tangents are denoted as follows:

Tangent to hyperbole

When the hyperbola has a center at the point x c e n t e r ; y c e n t e r and vertices x c e n t e r + α ; y c e n t e r and x c e n t e r - α ; y c e n t e r , the inequality x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 is given if with vertices x c e n t e r ; y c e n t e r + b and x c e n t e r ; y c e n t e r - b is then given by the inequality x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

A hyperbola can be represented as two combined functions of the form

y = b a (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 - a 2 + y c e n t e r or y = b a (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 + a 2 + y c e n t e r

In the first case, we have that the tangents are parallel to y, and in the second, they are parallel to x.

It follows that in order to find the equation of a tangent to a hyperbola, it is necessary to find out to which function the tangent point belongs. To determine this, it is necessary to make a substitution in the equations and check them for identity.

Example 7

Write the equation of the tangent to the hyperbola x - 3 2 4 - y + 3 2 9 = 1 at point 7; - 3 3 - 3 .

Solution

It is necessary to transform the record of the solution of finding the hyperbola using 2 functions. We get that

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 or y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

It is necessary to find out which function the given point with coordinates 7 belongs to; - 3 3 - 3 .

Obviously, to check the first function, it is necessary y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , then the point does not belong to the graph, since the equality is not satisfied.

For the second function, we have that y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , which means that the point belongs to the given graph. From here you should find the slope coefficient.

We get that

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Answer: the tangent equation can be represented as

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

It is visualized as follows:

Tangent to parabola

To compose the equation of the tangent to the parabola y \u003d a x 2 + b x + c at the point x 0, y (x 0) , you must use the standard algorithm, then the equation will take the form y \u003d y "(x 0) x - x 0 + y ( x 0) Such a tangent at the vertex is parallel to x.

The parabola x = a y 2 + b y + c should be defined as the union of two functions. Therefore, we need to solve the equation for y. We get that

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Let's graph it as:

To find out whether a point x 0 , y (x 0) belongs to a function, gently follow the standard algorithm. Such a tangent will be parallel to y with respect to the parabola.

Example 8

Write the equation of the tangent to the graph x - 2 y 2 - 5 y + 3 when we have a tangent slope of 150 °.

Solution

We start the solution by representing the parabola as two functions. We get that

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

The value of the slope is equal to the value of the derivative at the point x 0 of this function and is equal to the tangent of the slope.

We get:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

From here we determine the value of x for the touch points.

The first function will be written as

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Obviously, there are no real roots, since we got a negative value. We conclude that there is no tangent with an angle of 150 ° for such a function.

The second function will be written as

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

We have that the touch points - 23 4 ; - 5 + 3 4 .

Answer: the tangent equation takes the form

y = - 1 3 x - 23 4 + - 5 + 3 4

Let's graph it like this:

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

Y \u003d f (x) and if at this point a tangent can be drawn to the function graph that is not perpendicular to the abscissa axis, then the slope of the tangent is f "(a). We have already used this several times. For example, in § 33 it was established, that the graph of the function y \u003d sin x (sinusoid) at the origin forms an angle of 45 ° with the abscissa axis (more precisely, the tangent to the graph at the origin makes an angle of 45 ° with the positive direction of the x axis), and in example 5 of § 33 points were found on given schedule functions, in which the tangent is parallel to the x-axis. In example 2 of § 33, an equation was drawn up for the tangent to the graph of the function y \u003d x 2 at the point x \u003d 1 (more precisely, at the point (1; 1), but more often only the value of the abscissa is indicated, assuming that if the value of the abscissa is known, then the value of the ordinate can be found from the equation y = f(x)). In this section, we will develop an algorithm for compiling the equation of the tangent to the graph of any function.

Let the function y \u003d f (x) and the point M (a; f (a)) be given, and it is also known that f "(a) exists. Let us compose the equation of the tangent to the graph of the given function at a given point. This equation is like the equation of any straight line, not parallel to the y-axis, has the form y = kx + m, so the problem is to find the values ​​of the coefficients k and m.

There are no problems with the slope k: we know that k \u003d f "(a). To calculate the value of m, we use the fact that the desired line passes through the point M (a; f (a)). This means that if we substitute the coordinates points M into the equation of a straight line, we get the correct equality: f (a) \u003d ka + m, from where we find that m \u003d f (a) - ka.
It remains to substitute the found values ​​of the whale coefficients into the equation straight:

We have obtained the equation of the tangent to the graph of the function y \u003d f (x) at the point x \u003d a.
If, say,
Substituting in equation (1) the found values ​​a \u003d 1, f (a) \u003d 1 f "(a) \u003d 2, we get: y \u003d 1 + 2 (x-f), i.e. y \u003d 2x-1.
Compare this result with the one obtained in Example 2 of § 33. Naturally, the same thing happened.
Let us compose the equation of the tangent to the graph of the function y \u003d tg x at the origin. We have: hence cos x f "(0) = 1. Substituting the found values ​​a \u003d 0, f (a) \u003d 0, f "(a) \u003d 1 into equation (1), we get: y \u003d x.
That is why we drew the tangentoid in § 15 (see Fig. 62) through the origin of coordinates at an angle of 45 ° to the abscissa axis.
Solving these rather simple examples, we actually used a certain algorithm, which is embedded in formula (1). Let's make this algorithm explicit.

ALGORITHM FOR COMPOSING THE EQUATION OF THE FUNCTION TANGENT TO THE GRAPH y \u003d f (x)

1) Designate the abscissa of the point of contact with the letter a.
2) Calculate 1 (a).
3) Find f "(x) and calculate f" (a).
4) Substitute the found numbers a, f(a), (a) into formula (1).

Example 1 Write an equation for the tangent to the graph of the function at the point x = 1.
Let's use the algorithm, considering that in this example

On fig. 126 shows a hyperbola, a straight line y \u003d 2x is built.
The drawing confirms the above calculations: indeed, the line y \u003d 2-x touches the hyperbola at the point (1; 1).

Answer: y \u003d 2-x.
Example 2 Draw a tangent to the graph of the function so that it is parallel to the straight line y \u003d 4x - 5.
Let us refine the formulation of the problem. The requirement to "draw a tangent" usually means "make an equation for a tangent". This is logical, because if a person was able to compose an equation for a tangent, then he is unlikely to experience difficulties in constructing a straight line on the coordinate plane according to its equation.
Let's use the algorithm for compiling the tangent equation, considering that in this example, But, unlike the previous example, there is ambiguity here: the abscissa of the tangent point is not explicitly indicated.
Let's start talking like this. The desired tangent must be parallel to the straight line y \u003d 4x-5. Two lines are parallel if and only if their slopes are equal. This means that the slope of the tangent must be equal to the slope of the given straight line: Thus, we can find the value of a from the equation f "(a) \u003d 4.
We have:
From the equation So, there are two tangents that satisfy the conditions of the problem: one at the point with the abscissa 2, the other at the point with the abscissa -2.
Now you can act according to the algorithm.

Example 3 From the point (0; 1) draw a tangent to the graph of the function
Let's use the algorithm for compiling the tangent equation, considering that in this example Note that here, as in example 2, the abscissa of the tangent point is not explicitly indicated. Nevertheless, we act according to the algorithm.

By condition, the tangent passes through the point (0; 1). Substituting into equation (2) the values ​​x = 0, y = 1, we get:
As you can see, in this example, only at the fourth step of the algorithm we managed to find the abscissa of the touch point. Substituting the value a \u003d 4 into equation (2), we get:

On fig. 127 shows a geometric illustration of the considered example: a graph of the function

In § 32 we noted that for a function y = f(x), which has a derivative at a fixed point x, the approximate equality holds:

For the convenience of further reasoning, we change the notation: instead of x we ​​will write a, instead we will write x, and accordingly we will write x-a instead. Then the approximate equality written above will take the form:

Now take a look at fig. 128. A tangent is drawn to the graph of the function y \u003d f (x) at the point M (a; f (a)). Point x is marked on the x-axis close to a. It is clear that f(x) is the ordinate of the graph of the function at the specified point x. And what is f (a) + f "(a) (x-a)? This is the ordinate of the tangent corresponding to the same point x - see formula (1). What is the meaning of approximate equality (3)? That to calculate the approximate value of the function, the value of the tangent ordinate is taken.

Example 4 Find the approximate value of the numerical expression 1.02 7 .
We are talking about finding the value of the function y \u003d x 7 at the point x \u003d 1.02. We use formula (3), taking into account that in this example
As a result, we get:

If we use a calculator, we get: 1.02 7 = 1.148685667...
As you can see, the approximation accuracy is quite acceptable.
Answer: 1,02 7 =1,14.

A.G. Mordkovich Algebra Grade 10

Calendar-thematic planning in mathematics, video in mathematics online, Math at school download

Lesson content lesson summary support frame lesson presentation accelerative methods interactive technologies Practice tasks and exercises self-examination workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photographs, pictures graphics, tables, schemes humor, anecdotes, jokes, comics parables, sayings, crossword puzzles, quotes Add-ons abstracts articles chips for inquisitive cribs textbooks basic and additional glossary of terms other Improving textbooks and lessonscorrecting errors in the textbook updating a fragment in the textbook elements of innovation in the lesson replacing obsolete knowledge with new ones Only for teachers perfect lessons calendar plan for the year methodological recommendations of the discussion program Integrated Lessons

Tangent is a straight line , which touches the graph of the function at one point and all points of which are at the smallest distance from the graph of the function. Therefore, the tangent passes tangent to the function graph at a certain angle and several tangents cannot pass through the tangent point at different angles. The tangent equations and the equations of the normal to the graph of the function are compiled using the derivative.

The tangent equation is derived from the straight line equation .

We derive the equation of the tangent, and then the equation of the normal to the graph of the function.

y = kx + b .

In him k- angular coefficient.

From here we get the following entry:

y - y 0 = k(x - x 0 ) .

Derivative value f "(x 0 ) functions y = f(x) at the point x0 equal to the slope k=tg φ tangent to the graph of a function drawn through a point M0 (x 0 , y 0 ) , where y0 = f(x 0 ) . This is what geometric meaning of the derivative .

Thus, we can replace k on the f "(x 0 ) and get the following the equation of the tangent to the graph of the function :

y - y 0 = f "(x 0 )(x - x 0 ) .

In tasks for compiling the equation of a tangent to the graph of a function (and we will soon move on to them), it is required to bring the equation obtained from the above formula to general equation of a straight line. To do this, you need to transfer all the letters and numbers to the left side of the equation, and leave zero on the right side.

Now about the normal equation. Normal is a straight line passing through the tangent point to the graph of the function perpendicular to the tangent. Normal Equation :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

To warm up the first example, you are asked to solve it yourself, and then look at the solution. There is every reason to hope that this task will not be a "cold shower" for our readers.

Example 0. Compose the equation of the tangent and the equation of the normal to the graph of the function at a point M (1, 1) .

Example 1 Compose the equation of the tangent and the equation of the normal to the graph of the function , if the abscissa of the touch point is .

Let's find the derivative of the function:

Now we have everything that needs to be substituted into the notation given in the theoretical reference in order to obtain the tangent equation. We get

In this example, we were lucky: the slope turned out to be equal to zero, so there was no need to separately bring the equation to a general form. Now we can write the normal equation:

In the figure below: a graph of a function in burgundy, a tangent in green, a normal in orange.

The next example is also not complicated: the function, as in the previous one, is also a polynomial, but the angular coefficient will not be equal to zero, so one more step will be added - bringing the equation to a general form.

Example 2

Solution. Let's find the ordinate of the touch point:

Let's find the derivative of the function:

.

Let's find the value of the derivative at the point of contact, that is, the slope of the tangent:

We substitute all the data obtained into the "blank formula" and get the tangent equation:

We bring the equation to a general form (we collect all letters and numbers other than zero on the left side, and leave zero on the right side):

We compose the equation of the normal:

Example 3 Compose the equation of the tangent and the equation of the normal to the graph of the function if the abscissa of the point of contact is .

Solution. Let's find the ordinate of the touch point:

Let's find the derivative of the function:

.

Let's find the value of the derivative at the point of contact, that is, the slope of the tangent:

.

We find the equation of the tangent:

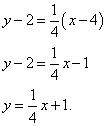
Before bringing the equation to a general form, you need to “combine” it a little: multiply term by term by 4. We do this and bring the equation to a general form:

We compose the equation of the normal:

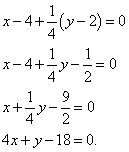
Example 4 Compose the equation of the tangent and the equation of the normal to the graph of the function if the abscissa of the point of contact is .

Solution. Let's find the ordinate of the touch point:

.

Let's find the derivative of the function:

Let's find the value of the derivative at the point of contact, that is, the slope of the tangent:

.

We get the tangent equation:

We bring the equation to a general form:

We compose the equation of the normal:

A common mistake when writing tangent and normal equations is not to notice that the function given in the example is complex and calculate its derivative as the derivative of a simple function. The following examples are already complex functions(the corresponding lesson will open in a new window).

Example 5 Compose the equation of the tangent and the equation of the normal to the graph of the function if the abscissa of the point of contact is .

Solution. Let's find the ordinate of the touch point:

Attention! This function is complex, since the argument of the tangent (2 x) is itself a function. Therefore, we find the derivative of a function as the derivative of a complex function.

Example 1 Given a function f(x) = 3x 2 + 4x– 5. Let's write the equation of the tangent to the graph of the function f(x) at the point of the graph with the abscissa x 0 = 1.

Solution. Function derivative f(x) exists for any x R . Let's find it:

= (3x 2 + 4x– 5)′ = 6 x + 4.

Then f(x 0) = f(1) = 2; (x 0) = = 10. The tangent equation has the form:

y = (x 0) (x – x 0) + f(x 0),

y = 10(x – 1) + 2,

y = 10x – 8.

Answer. y = 10x – 8.

Example 2 Given a function f(x) = x 3 – 3x 2 + 2x+ 5. Let's write the equation of the tangent to the graph of the function f(x), parallel to the line y = 2x – 11.

Solution. Function derivative f(x) exists for any x R . Let's find it:

= (x 3 – 3x 2 + 2x+ 5)′ = 3 x 2 – 6x + 2.

Since the tangent to the graph of the function f(x) at the point with the abscissa x 0 is parallel to the line y = 2x– 11, then its slope is 2, i.e. ( x 0) = 2. Find this abscissa from the condition that 3 x– 6x 0 + 2 = 2. This equality is valid only for x 0 = 0 and x 0 = 2. Since in both cases f(x 0) = 5, then the straight line y = 2x + b touches the graph of the function either at the point (0; 5) or at the point (2; 5).

In the first case, the numerical equality is true 5 = 2×0 + b, where b= 5, and in the second case, the numerical equality is true 5 = 2 × 2 + b, where b = 1.

So there are two tangents y = 2x+ 5 and y = 2x+ 1 to the graph of the function f(x) parallel to the line y = 2x – 11.

Answer. y = 2x + 5, y = 2x + 1.

Example 3 Given a function f(x) = x 2 – 6x+ 7. Let's write the equation of the tangent to the graph of the function f(x) passing through the point A (2; –5).

Solution. Because f(2) –5, then the point A does not belong to the graph of the function f(x). Let x 0 - abscissa of the touch point.

Function derivative f(x) exists for any x R . Let's find it:

= (x 2 – 6x+ 1)′ = 2 x – 6.

Then f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 - 6. The tangent equation has the form:

y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,

y = (2x 0 – 6)x– x+ 7.

Since the point A belongs to the tangent, then the numerical equality is true

–5 = (2x 0 – 6)×2– x+ 7,

where x 0 = 0 or x 0 = 4. This means that through the point A it is possible to draw two tangents to the graph of the function f(x).

If a x 0 = 0, then the tangent equation has the form y = –6x+ 7. If x 0 = 4, then the tangent equation has the form y = 2x – 9.

Answer. y = –6x + 7, y = 2x – 9.

Example 4 Given functions f(x) = x 2 – 2x+ 2 and g(x) = –x 2 - 3. Let's write the equation of the common tangent to the graphs of these functions.

Solution. Let x 1 - abscissa of the point of contact of the desired line with the graph of the function f(x), a x 2 - abscissa of the point of contact of the same line with the graph of the function g(x).

Function derivative f(x) exists for any x R . Let's find it:

= (x 2 – 2x+ 2)′ = 2 x – 2.

Then f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 - 2. The tangent equation has the form:

y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,

y = (2x 1 – 2)x – x+ 2. (1)

Let's find the derivative of the function g(x):

= (–x 2 – 3)′ = –2 x.

The video tutorial "The equation of the tangent to the graph of a function" demonstrates educational material for mastering the topic. During the video lesson, the theoretical material necessary for the formation of the concept of the equation of the tangent to the graph of a function at a given point is presented, the algorithm for finding such a tangent, examples of solving problems using the studied theoretical material are described.

The video tutorial uses methods that improve the visibility of the material. Drawings, diagrams are inserted in the view, important voice comments are given, animation, color highlighting and other tools are applied.

The video lesson begins with the presentation of the topic of the lesson and the image of a tangent to the graph of some function y=f(x) at the point M(a;f(a)). It is known that the slope of the tangent drawn to the graph at a given point is equal to the derivative of the function f΄(a) at a given point. Also from the course of algebra, the equation of the straight line y=kx+m is known. The solution of the problem of finding the tangent equation at a point is schematically presented, which reduces to finding the coefficients k, m. Knowing the coordinates of the point belonging to the graph of the function, we can find m by substituting the value of the coordinates into the equation of the tangent f(a)=ka+m. From it we find m=f(a)-ka. Thus, knowing the value of the derivative at a given point and the coordinates of the point, we can represent the tangent equation in this way y=f(a)+f΄(a)(x-a).

The following is an example of drawing up a tangent equation, following the scheme. Given a function y=x 2 , x=-2. Having accepted a=-2, we find the value of the function at this point f(a)= f(-2)=(-2) 2 =4. We determine the derivative of the function f΄(х)=2х. At this point, the derivative is equal to f΄(a)= f΄(-2)=2 (-2)=-4. To compile the equation, all coefficients a=-2, f(a)=4, f΄(a)=-4 are found, so the tangent equation y=4+(-4)(x+2). Simplifying the equation, we get y \u003d -4-4x.

In the following example, it is proposed to formulate the equation of the tangent at the origin to the graph of the function y=tgx. At this point a=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. So the tangent equation looks like y=x.

As a generalization, the process of compiling the equation of the tangent to the function graph at some point is formalized as an algorithm consisting of 4 steps:

• A designation is introduced for the abscissa of the point of contact;
• f(a) is calculated;
• F΄(х) is determined and f΄(a) is calculated. The found values ​​a, f(a), f΄(a) are substituted into the formula of the tangent equation y=f(a)+f΄(a)(x-a).

Example 1 considers the compilation of the equation of the tangent to the graph of the function y \u003d 1 / x at the point x \u003d 1. We use an algorithm to solve the problem. For this function at the point a=1, the value of the function f(a)=-1. Derivative of the function f΄(х)=1/х 2 . At the point a=1, the derivative f΄(a)= f΄(1)=1. Using the data obtained, the equation of the tangent y \u003d -1 + (x-1), or y \u003d x-2, is compiled.

In example 2, you need to find the equation of the tangent to the graph of the function y \u003d x 3 +3x 2 -2x-2. The main condition is the parallelism of the tangent and the straight line y \u003d -2x + 1. First, we find the slope of the tangent, equal to the slope of the straight line y \u003d -2x + 1. Since f΄(a)=-2 for this straight line, then k=-2 for the desired tangent. We find the derivative of the function (x 3 + 3x 2 -2x-2) ΄ \u003d 3x 2 + 6x-2. Knowing that f΄(a)=-2, we find the coordinates of the point 3а 2 +6а-2=-2. Solving the equation, we get a 1 \u003d 0, and 2 \u003d -2. Using the found coordinates, you can find the tangent equation using a well-known algorithm. We find the value of the function at the points f(a 1)=-2, f(a 2)=-18. The value of the derivative at the point f΄(а 1)= f΄(а 2)=-2. Substituting the found values ​​into the tangent equation, we obtain for the first point a 1 \u003d 0 y \u003d -2x-2, and for the second point a 2 \u003d -2 the tangent equation y \u003d -2x-22.

Example 3 describes the formulation of the tangent equation for its drawing at the point (0;3) to the graph of the function y=√x. The decision is made according to the known algorithm. The touch point has coordinates x=a, where a>0. The value of the function at the point f(a)=√x. The derivative of the function f΄(х)=1/2√х, therefore, at the given point f΄(а)=1/2√а. Substituting all the obtained values ​​into the tangent equation, we get y \u003d √a + (x-a) / 2√a. Transforming the equation, we get y=x/2√a+√a/2. Knowing that the tangent passes through the point (0; 3), we find the value of a. Find a from 3=√a/2. Hence √a=6, a=36. We find the equation of the tangent y \u003d x / 12 + 3. The figure shows the graph of the function under consideration and the constructed desired tangent.

Students are reminded of the approximate equalities Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx. Taking x=a, x+Δx=x, Δx=x-a, we get f(x)- f(a)≈f΄(a)(x-a), hence f(x)≈f(a)+ f΄(a)(x-a).

In example 4, it is necessary to find the approximate value of the expression 2.003 6 . Since it is necessary to find the value of the function f (x) \u003d x 6 at the point x \u003d 2.003, we can use the well-known formula, taking f (x) \u003d x 6, a \u003d 2, f (a) \u003d f (2) \u003d 64, f ΄(x)=6х 5 . Derivative at point f΄(2)=192. Therefore, 2.003 6 ≈65-192 0.003. After calculating the expression, we get 2.003 6 ≈64.576.

The video lesson "The equation of the tangent to the graph of a function" is recommended for use in a traditional math lesson at school. For a distance learning teacher, the video material will help explain the topic more clearly. The video can be recommended for self-consideration by students if necessary to deepen their understanding of the subject.

TEXT EXPLANATION:

We know that if the point M (a; f (a)) (em with coordinates a and ef from a) belongs to the graph of the function y \u003d f (x) and if at this point a tangent can be drawn to the graph of the function, not perpendicular to the axis abscissa, then the slope of the tangent is f "(a) (ef stroke from a).

Let a function y = f(x) and a point M (a; f(a)) be given, and it is also known that f´(a) exists. Let's compose the equation of the tangent to the graph of a given function at a given point. This equation, like the equation of any straight line not parallel to the y-axis, has the form y = kx + m (y is equal to ka x plus em), so the task is to find the values ​​of the coefficients k and m. (ka and em)

Slope k \u003d f "(a). To calculate the value of m, we use the fact that the desired straight line passes through the point M (a; f (a)). This means that if we substitute the coordinates of the point M in the equation of the straight line, we get the correct equality : f(a) = ka+m, whence we find that m = f(a) - ka.

It remains to substitute the found values ​​of the coefficients ki and m into the equation of a straight line:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= f(a)+ f"(a) (x- a). ( Y is equal to eff from a plus ef stroke from a multiplied by x minus a).

We have obtained the equation of the tangent to the graph of the function y = f(x) at the point x=a.

If, say, y \u003d x 2 and x \u003d -2 (i.e. a \u003d -2), then f (a) \u003d f (-2) \u003d (-2) 2 \u003d 4; f´(x) \u003d 2x, so f "(a) \u003d f´(-2) \u003d 2 (-2) \u003d -4. (then eff from a is equal to four, eff prime from x is equal to two x, which means ef stroke from a equals minus four)

Substituting in the equation the found values ​​a \u003d -2, f (a) \u003d 4, f "(a) \u003d -4, we get: y \u003d 4 + (-4) (x + 2), i.e. y \u003d -4x -four.

(y equals minus four x minus four)

Let's compose the equation of the tangent to the graph of the function y \u003d tgx (y is equal to tangent x) at the origin. We have: a = 0, f(0) = tg0=0;

f"(x)= , so f"(0) = l. Substituting the found values ​​a=0, f(a)=0, f´(a) = 1 into the equation, we get: y=x.

We generalize our steps for finding the equation of the tangent to the graph of the function at the point x using the algorithm.

ALGORITHM FOR COMPOSING THE EQUATION OF THE FUNCTION tangent to the GRAPH y \u003d f (x):

1) Designate the abscissa of the point of contact with the letter a.

2) Calculate f(a).

3) Find f´(x) and calculate f´(a).

4) Substitute the found numbers a, f(a), f´(a) into the formula y= f(a)+ f"(a) (x- a).

Example 1. Write the equation of the tangent to the graph of the function y \u003d - in

point x = 1.

Solution. Let's use the algorithm, considering that in this example

2) f(a)=f(1)=-=-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) Substitute the three numbers found: a \u003d 1, f (a) \u003d -1, f "(a) \u003d 1 into the formula. We get: y \u003d -1 + (x-1), y \u003d x-2.

Answer: y = x-2.

Example 2. Given a function y = x 3 +3x 2 -2x-2. Write the equation of the tangent to the graph of the function y \u003d f (x), parallel to the straight line y \u003d -2x +1.

Using the algorithm for compiling the tangent equation, we take into account that in this example f(x) = x 3 +3x 2 -2x-2, but the abscissa of the touch point is not specified here.

Let's start talking like this. The desired tangent must be parallel to the straight line y \u003d -2x + 1. And parallel lines have equal slopes. Hence, the slope of the tangent is equal to the slope of the given straight line: k cas. = -2. Hok cas. = f "(a). Thus, we can find the value of a from the equation f ´ (a) \u003d -2.

Let's find the derivative of the function y=f(x):

f"(x) \u003d (x 3 + 3x 2 -2x-2)´ \u003d 3x 2 + 6x-2;f"(a) \u003d 3a 2 + 6a-2.

From the equation f "(a) \u003d -2, i.e. 3а 2 +6а-2\u003d -2 we find a 1 \u003d 0, a 2 \u003d -2. This means that there are two tangents that satisfy the conditions of the problem: one at a point with abscissa 0, the other at a point with abscissa -2.

Now you can act according to the algorithm.

1) a 1 \u003d 0, and 2 \u003d -2.

2) f(a 1) = 0 3 +3 0 2 -2∙0-2=-2; f(a2)= (-2) 3 +3 (-2) 2 -2 (-2)-2=6;

3) f "(a 1) = f" (a 2) = -2.

4) Substituting the values ​​a 1 = 0, f (a 1) = -2, f "(a 1) = -2 into the formula, we get:

y=-2-2(x-0), y=-2x-2.

Substituting the values ​​a 2 \u003d -2, f (a 2) \u003d 6, f "(a 2) \u003d -2 into the formula, we get:

y=6-2(x+2), y=-2x+2.

Answer: y=-2x-2, y=-2x+2.

Example 3. From the point (0; 3) draw a tangent to the graph of the function y \u003d. Solution. Let's use the algorithm for compiling the tangent equation, given that in this example f(x) = . Note that here, as in Example 2, the abscissa of the touch point is not explicitly indicated. Nevertheless, we act according to the algorithm.

1) Let x = a be the abscissa of the point of contact; it is clear that a > 0.

3) f´(x)=()´=; f´(a) =.

4) Substituting the values ​​a, f(a) = , f "(a) = into the formula

y \u003d f (a) + f "(a) (x-a), we get:

By condition, the tangent passes through the point (0; 3). Substituting the values ​​x = 0, y = 3 into the equation, we get: 3 = , and then =6, a =36.

As you can see, in this example, only at the fourth step of the algorithm we managed to find the abscissa of the touch point. Substituting the value a =36 into the equation, we get: y=+3

On fig. Figure 1 presents a geometric illustration of the considered example: a graph of the function y \u003d is plotted, a straight line y \u003d +3 is drawn.

Answer: y = +3.

We know that for the function y = f(x), which has a derivative at the point x, the approximate equality is true: Δyf´(x)Δx

or, in more detail, f(x+Δx)-f(x) f´(x) Δx (ef from x plus delta x minus ef from x is approximately equal to ef prime from x to delta x).

For the convenience of further reasoning, we change the notation:

instead of x we ​​will write a,

instead of x + Δx we will write x

instead of Δx we will write x-a.

Then the approximate equality written above will take the form:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (ef from x is approximately equal to eff from a plus ef stroke from a, multiplied by the difference between x and a).

Example 4. Find the approximate value of the numerical expression 2.003 6 .

Solution. We are talking about finding the value of the function y \u003d x 6 at the point x \u003d 2.003. Let's use the formula f(x)f(a)+f´(a)(x-a), considering that in this example f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 =64; x \u003d 2.003, f "(x) \u003d 6x 5 and, therefore, f" (a) \u003d f "(2) \u003d 6 2 5 \u003d 192.

As a result, we get:

2.003 6 64+192 0.003, i.e. 2.003 6 = 64.576.

If we use a calculator, we get:

2,003 6 = 64,5781643...

As you can see, the approximation accuracy is quite acceptable.