Opće teoreme o dinamici sistema tijela. Teoreme o kretanju centra mase, o promjeni količine gibanja, o promjeni glavnog ugaonog momenta, o promjeni kinetičke energije. D'Alembertovi principi i mogući pokreti. Opća jednadžba dinamike. Lagrangeove jednadžbe.

Opće teoreme o dinamici krutog tijela i sistema tijela

Opće teoreme dinamike- ovo je teorema o kretanju centra mase mehaničkog sistema, teorema o promjeni količine gibanja, teorema o promjeni glavnog ugaonog momenta (kinetičkog momenta) i teorema o promjeni kinetičke energije mehaničkog sistema.

Teorema o kretanju centra mase mehaničkog sistema

Teorema o kretanju centra masa.
Proizvod mase sistema i ubrzanja njegovog centra mase jednak je vektorskom zbiru svih vanjskih sila koje djeluju na sistem:
.

Ovdje je M masa sistema:
;
a C je ubrzanje centra mase sistema:
;
v C - brzina centra mase sistema:
;
r C - radijus vektor (koordinate) centra mase sistema:
;
- koordinate (u odnosu na fiksni centar) i mase tačaka koje čine sistem.

Teorema o promjeni impulsa (momenta)

Količina kretanja (impulsa) sistema jednak je proizvodu mase čitavog sistema brzinom njegovog centra mase ili zbirom impulsa (zbir impulsa) pojedinih tačaka ili delova koji čine sistem:
.

Teorema o promjeni impulsa u diferencijalnom obliku.
Vremenski izvod količine kretanja (momenta) sistema jednak je vektorskom zbiru svih vanjskih sila koje djeluju na sistem:
.

Teorema o promjeni impulsa u integralnom obliku.
Promjena impulsa (impulsa) sistema u određenom vremenskom periodu jednaka je zbiru impulsa vanjskih sila u istom vremenskom periodu:
.

Zakon održanja količine gibanja (momenta).
Ako je zbir svih vanjskih sila koje djeluju na sistem jednak nuli, tada će vektor zamaha sistema biti konstantan. Odnosno, sve njegove projekcije na koordinatne ose održavat će konstantne vrijednosti.

Ako je zbir projekcija vanjskih sila na bilo koju osu nula, tada će projekcija količine kretanja sistema na ovu osu biti konstantna.

Teorema o promjeni glavnog ugaonog momenta (teorema o momentima)

Glavni ugaoni moment sistema u odnosu na dati centar O je veličina jednaka vektorskom zbroju ugaonog momenta svih tačaka sistema u odnosu na ovaj centar:
.
Ovdje uglaste zagrade označavaju unakrsni proizvod.

Priključeni sistemi

Sljedeća teorema se primjenjuje na slučaj kada mehanički sistem ima fiksnu tačku ili osu koja je fiksirana u odnosu na inercijski referentni okvir. Na primjer, tijelo osigurano sfernim ležajem. Ili sistem tijela koji se kreće oko fiksnog centra. Takođe može biti fiksna osa oko koje se rotira tijelo ili sistem tijela. U ovom slučaju, momente treba shvatiti kao momente impulsa i sila u odnosu na fiksnu osu.

Teorema o promjeni glavnog ugaonog momenta (teorema o momentima)
Vremenski izvod glavnog ugaonog momenta sistema u odnosu na neki fiksni centar O jednak je zbiru momenata svih spoljnih sila sistema u odnosu na isti centar.

Zakon održanja glavnog ugaonog momenta (kutnog momenta).
Ako je zbir momenata svih vanjskih sila primijenjenih na sistem u odnosu na dati fiksni centar O jednak nuli, tada će glavni ugaoni moment sistema u odnosu na ovaj centar biti konstantan. Odnosno, sve njegove projekcije na koordinatne ose održavat će konstantne vrijednosti.

Ako je zbroj momenata vanjskih sila u odnosu na neku fiksnu osu jednak nuli, tada će ugaoni moment sistema u odnosu na ovu osu biti konstantan.

Proizvoljni sistemi

Sljedeća teorema ima univerzalni karakter. Primjenjuje se i na fiksne i na slobodno pokretne sisteme. U slučaju fiksnih sistema, potrebno je uzeti u obzir reakcije veza na fiksnim tačkama. Razlikuje se od prethodne teoreme po tome što umjesto fiksne tačke O treba uzeti centar mase C sistema.

Teorema momenata o centru masa
Vremenski izvod glavnog ugaonog momenta sistema u odnosu na centar mase C jednak je zbiru momenata svih spoljnih sila sistema u odnosu na isti centar.

Zakon održanja ugaonog momenta.
Ako je zbir momenata svih vanjskih sila primijenjenih na sistem u odnosu na centar mase C jednak nuli, tada će glavni moment količine kretanja sistema u odnosu na ovaj centar biti konstantan. Odnosno, sve njegove projekcije na koordinatne ose održavat će konstantne vrijednosti.

Moment inercije tijela

Ako se tijelo rotira oko z ose sa ugaonom brzinom ω z, tada se njegov ugaoni moment (kinetički moment) u odnosu na osu z određuje formulom:
L z = J z ω z ,
gdje je J z moment inercije tijela u odnosu na osu z.

Moment inercije tijela u odnosu na osu z određena formulom:
,
gdje je h k udaljenost od tačke mase m k do ose z.
Za tanak prsten mase M i poluprečnika R, ili cilindar čija je masa raspoređena duž njegovog ruba,
J z = M R 2 .
Za čvrsti homogeni prsten ili cilindar,
.

Steiner-Huygens teorem.
Neka je Cz osa koja prolazi kroz centar mase tijela, a Oz osa paralelna s njim. Tada su momenti inercije tijela u odnosu na ove ose povezani relacijom:
J Oz = J Cz + M a 2 ,
gdje je M tjelesna težina; a je rastojanje između osa.

U opštijem slučaju:
,
gdje je tenzor inercije tijela.
Ovdje je vektor povučen iz centra mase tijela do tačke mase m k.

Teorema o promjeni kinetičke energije

Neka tijelo mase M vrši translacijsko i rotacijsko kretanje s ugaonom brzinom ω oko neke ose z. Tada se kinetička energija tijela određuje formulom:
,
gdje je v C brzina kretanja centra mase tijela;
J Cz je moment inercije tijela u odnosu na osu koja prolazi kroz centar mase tijela paralelno s osom rotacije. Smjer ose rotacije se može promijeniti tokom vremena. Ova formula daje trenutnu vrijednost kinetičke energije.

Teorema o promjeni kinetičke energije sistema u diferencijalnom obliku.
Diferencijal (prirast) kinetičke energije sistema tokom nekog kretanja jednak je zbiru diferencijala rada na ovom kretanju svih spoljašnjih i unutrašnjih sila koje se primenjuju na sistem:
.

Teorema o promjeni kinetičke energije sistema u integralnom obliku.
Promjena kinetičke energije sistema pri nekom kretanju jednaka je zbiru rada na ovom kretanju svih vanjskih i unutrašnjih sila primijenjenih na sistem:
.

Posao koji je izvršila sila, jednak je skalarnom proizvodu vektora sila i beskonačno malog pomaka točke njegove primjene:
,
odnosno proizvod apsolutnih vrijednosti vektora F i ds kosinusom ugla između njih.

Rad obavljen momentom sile, jednak je skalarnom proizvodu vektora momenta i beskonačno malog ugla rotacije:
.

d'Alambertov princip

Suština d'Alamberovog principa je da se problemi dinamike svedu na probleme statike. Da bi se to postiglo, pretpostavlja se (ili je unaprijed poznato) da tijela sistema imaju određena (ugaona) ubrzanja. Zatim se uvode inercijalne sile i (ili) momenti inercijskih sila, koji su po veličini jednaki i suprotni po smjeru silama i momentima sila koje bi, prema zakonima mehanike, stvorile zadana ubrzanja ili kutna ubrzanja.

Pogledajmo primjer. Tijelo je podvrgnuto translacijskom kretanju i na njega djeluju vanjske sile. Dalje pretpostavljamo da ove sile stvaraju ubrzanje centra mase sistema. Prema teoremi o kretanju centra mase, centar mase tijela imao bi isto ubrzanje da na tijelo djeluje sila. Zatim uvodimo silu inercije:
.
Nakon ovoga, problem dinamike:
.
;
.

Za rotacijsko kretanje postupite na isti način. Neka tijelo rotira oko z ose i na njega djeluju vanjski momenti sile M e zk . Pretpostavljamo da ovi momenti stvaraju ugaono ubrzanje ε z. Zatim uvodimo moment sile inercije M I = - J z ε z. Nakon ovoga, problem dinamike:
.
Pretvara se u problem statike:
;
.

Princip mogućih pokreta

Za rješavanje statičkih problema koristi se princip mogućih pomaka. U nekim problemima daje kraće rješenje od sastavljanja jednadžbi ravnoteže. Ovo posebno važi za sisteme sa vezama (na primer, sisteme tela povezanih nitima i blokovima) koji se sastoje od mnogo tela

Princip mogućih pokreta.
Za ravnotežu mehaničkog sistema sa idealnim vezama potrebno je i dovoljno da zbir elementarnih radova svih aktivnih sila koje na njega deluju za svako moguće kretanje sistema bude jednak nuli.

Moguće preseljenje sistema- ovo je mali pokret u kojem se ne prekidaju veze nametnute sistemu.

Idealne veze- to su veze koje ne rade kada se sistem kreće. Tačnije, količina posla koju obavljaju same veze pri pomicanju sistema je nula.

Opća jednadžba dinamike (D'Alembert - Lagrangeov princip)

D'Alembert-Lagrangeov princip je kombinacija D'Alembertovog principa sa principom mogućih kretanja. Odnosno, pri rješavanju dinamičkog problema uvodimo inercijalne sile i problem svodimo na statički problem, koji rješavamo po principu mogućih pomaka.

D'Alembert-Lagrangeov princip.
Kada se mehanički sistem sa idealnim vezama kreće, u svakom trenutku vremena zbir elementarnih radova svih primenjenih aktivnih sila i svih inercijskih sila na bilo koje moguće kretanje sistema je nula:
.
Ova jednačina se zove opšta jednačina dinamike.

Lagrangeove jednadžbe

Generalizirane q koordinate 1 , q 2 , ..., q n je skup od n veličina koje jedinstveno određuju položaj sistema.

Broj generalizovanih koordinata n poklapa se sa brojem stepeni slobode sistema.

Generalizirane brzine su derivati ​​generaliziranih koordinata u odnosu na vrijeme t.

Generalizovane sile Q 1 , Q 2 , ..., Q n .
Razmotrimo moguće kretanje sistema, pri kojem će koordinata q k dobiti kretanje δq k. Preostale koordinate ostaju nepromijenjene. Neka je δA k rad vanjskih sila tokom takvog kretanja. Onda
δA k = Q k δq k , ili
.

Ako se uz moguće kretanje sistema mijenjaju sve koordinate, tada rad vanjskih sila tokom takvog kretanja ima oblik:
δA = Q 1 δq 1 + Q 2 δq 2 + ... + Q n δq n.
Tada su generalizirane sile parcijalni derivati ​​rada na pomacima:
.

Za potencijalne snage sa potencijalom Π,
.

Lagrangeove jednadžbe- ovo su jednadžbe kretanja mehaničkog sistema u generaliziranim koordinatama:

Ovdje je T kinetička energija. To je funkcija generaliziranih koordinata, brzina i, moguće, vremena. Stoga je njegov parcijalni izvod također funkcija generaliziranih koordinata, brzina i vremena. Zatim, morate uzeti u obzir da su koordinate i brzine funkcije vremena. Stoga, da biste pronašli ukupni izvod s obzirom na vrijeme, morate primijeniti pravilo diferencijacije složene funkcije:
.

Reference:
S. M. Targ, Kratki kurs iz teorijske mehanike, “Viša škola”, 2010.

Razmotrimo kretanje određenog sistema materijalnih objekata u odnosu na fiksni koordinatni sistem. Kada sistem nije slobodan, onda se može smatrati slobodnim ako odbacimo veze koje su nametnute sistemu i zamijenimo njihovo djelovanje odgovarajućim reakcijama.

Podelimo sve sile koje se primenjuju na sistem na spoljašnje i unutrašnje; oba mogu uključivati ​​reakcije odbačenih

veze. Označimo i glavni vektor i glavni moment vanjskih sila u odnosu na tačku A.

1. Teorema o promjeni impulsa. Ako je količina kretanja sistema, onda (vidi)

odnosno važi teorema: vremenski izvod impulsa sistema jednak je glavnom vektoru svih vanjskih sila.

Zamjenom vektora kroz njegov izraz gdje je masa sistema, je brzina centra mase, jednačina (4.1) može dobiti drugačiji oblik:

Ova jednakost znači da se centar mase sistema kreće poput materijalne tačke čija je masa jednaka masi sistema i na koju se primjenjuje sila koja je geometrijski jednaka glavnom vektoru svih vanjskih sila sistema. Posljednja tvrdnja se zove teorema o kretanju centra mase (centra inercije) sistema.

Ako onda iz (4.1) slijedi da je vektor momenta konstantan po veličini i smjeru. Projektujući ga na koordinatnu osu, dobijamo tri skalarna prva integrala, diferencijalne jednadžbe dvostruke kapice sistema:

Ovi integrali se nazivaju integrali momenta. Kada je brzina centra mase konstantna, odnosno kreće se jednoliko i pravolinijski.

Ako je projekcija glavnog vektora vanjskih sila na bilo koju osu, na primjer na osu, jednaka nuli, tada imamo jedan prvi integral, ili ako su dvije projekcije glavnog vektora jednake nuli, tada postoje dvije integrali momenta.

2. Teorema o promjeni ugaonog momenta. Neka je A neka proizvoljna tačka u prostoru (pokretna ili stacionarna), koja se ne poklapa nužno ni sa jednom specifičnom materijalnom tačkom sistema tokom čitavog vremena kretanja. Njegovu brzinu u fiksnom koordinatnom sistemu označavamo sa Teorema o promeni kinetičkog momenta materijalnog sistema u odnosu na tačku A ima oblik

Ako je tačka A fiksna, onda jednakost (4.3) poprima jednostavniji oblik:

Ova jednakost izražava teoremu o varijaciji ugaonog momenta sistema u odnosu na fiksnu tačku: vremenski izvod ugaonog momenta sistema, izračunat u odnosu na neku fiksnu tačku, jednak je glavnom momentu svih vanjskih sila relativnih do ove tačke.

Ako je tada prema (4.4) vektor ugaonog momenta konstantan po veličini i smjeru. Projektujući ga na koordinatne ose, dobijamo skalarne prve integrale diferencijalnih jednačina dvostrukog sistema:

Ovi integrali se nazivaju integrali momenta ili integrali površine.

Ako se tačka A poklapa sa centrom mase sistema, tada prvi član na desnoj strani jednakosti (4.3) nestaje i teorema o promjeni ugaonog momenta ima isti oblik pisanja (4.4) kao u slučaju fiksnu tačku A. Imajte na umu (vidi. str. 4 § 3), da se u slučaju koji se razmatra, apsolutni ugaoni moment sistema na levoj strani jednakosti (4.4) može biti zamenjen jednakim ugaonim momentom sistema u svom kretanju u odnosu na centar mase.

Neka je neka konstantna osa ili osa konstantnog pravca koja prolazi kroz centar mase sistema, i neka je kinetički moment sistema u odnosu na ovu osu. Iz (4.4) slijedi da

gdje je moment vanjskih sila u odnosu na osu. Ako tokom cijelog kretanja imamo prvi integral

U radovima S.A. Chaplygina dobijeno je nekoliko generalizacija teoreme o promjeni kinetičkog momenta, koje su potom primijenjene za rješavanje niza problema o kotrljajućim kuglicama. Daljnje generalizacije teoreme o promjeni mehaničkog momenta i njihove primjene u problemima dinamike krutog tijela sadržane su u radovima. Glavni rezultati ovih radova odnose se na teoremu o promjeni kinetičkog momenta u odnosu na pokretni, koji stalno prolazi kroz neku pokretnu tačku A. Neka je jedinični vektor usmjeren duž ove ose. Množenjem skalarno sa obe strane jednakosti (4.3) i dodavanjem člana na njegova dva dela dobijamo

Kada je kinematički uslov ispunjen

Jednačina (4.5) slijedi iz (4.7). A ako je uslov (4.8) zadovoljen tokom čitavog kretanja, tada postoji prvi integral (4.6).

Ako su veze sistema idealne i dozvoljavaju, među virtualnim pomacima, rotaciju sistema kao krutog tijela oko ose i tada je glavni moment reakcije u odnosu na osu i jednak nuli, a zatim vrijednost na desna strana jednačine (4.5) predstavlja glavni moment svih vanjskih aktivnih sila u odnosu na osu i . Jednakost ovog momenta sa nulom i valjanost relacije (4.8) biće u razmatranom slučaju dovoljni uslovi za postojanje integrala (4.6).

Ako je smjer ose i konstantan, tada će se uvjet (4.8) zapisati u obliku

Ova jednakost znači da su projekcije brzine centra mase i brzine tačke A na osu i na ravan okomitu na nju paralelne. U radu S.A. Chaplygina, umjesto (4.9), potrebno je ispunjenje manje opšteg uslova gdje je X proizvoljna konstantna vrijednost.

Imajte na umu da uvjet (4.8) ne ovisi o izboru točke na . Zaista, neka je P proizvoljna tačka na osi. Onda

i zbog toga

U zaključku, napominjemo Rézalovu geometrijsku interpretaciju jednadžbi (4.1) i (4.4): apsolutni vektori brzina krajeva vektora i jednaki su, respektivno, glavnom vektoru i glavnom momentu svih vanjskih sila u odnosu na tačku A .

Predavanje 3. Opće teoreme dinamike

Dinamika sistema materijalnih tačaka je važna grana teorijske mehanike. Ovdje uglavnom razmatramo probleme o kretanju mehaničkih sistema (sistema materijalnih tačaka) sa konačnim brojem stupnjeva slobode – maksimalnim brojem nezavisnih parametara koji određuju položaj sistema. Glavni zadatak dinamike sistema je proučavanje zakona kretanja krutog tijela i mehaničkih sistema.

Najjednostavniji pristup proučavanju kretanja sistema koji se sastoji od N materijalnih tačaka, svodi se na razmatranje kretanja svake pojedinačne tačke sistema. U tom slučaju moraju se odrediti sve sile koje djeluju na svaku tačku sistema, uključujući sile interakcije između tačaka.

Određivanjem ubrzanja svake tačke u skladu sa drugim Newtonovim zakonom (1.2), dobijamo za svaku tačku tri skalarna diferencijalna zakona kretanja drugog reda, tj. 3 N diferencijalni zakoni kretanja za čitav sistem.

Da bi se pronašle jednačine kretanja mehaničkog sistema na osnovu datih sila i početnih uslova za svaku tačku sistema, moraju se integrisati rezultujući diferencijalni zakoni. Ovaj problem je težak čak iu slučaju dve materijalne tačke koje se kreću samo pod uticajem interakcijskih sila po zakonu univerzalne privlačnosti (problem dva tela), a izuzetno težak u slučaju tri tačke interakcije (problem tri tela). ).

Stoga je potrebno pronaći metode za rješavanje problema koje bi dovele do rješivih jednačina i dale predstavu o kretanju mehaničkog sistema. Opšte teoreme dinamike, kao posljedica diferencijalnih zakona kretanja, omogućavaju nam da izbjegnemo složenost koja nastaje prilikom integracije i dobijemo potrebne rezultate.

3. 1. Opće napomene

Brojaćemo tačke mehaničkog sistema indeksima i, j, k itd., koji prolaze kroz sve vrijednosti 1, 2, 3… N, Gdje N – broj bodova sistema. Fizičke veličine koje se odnose na k Tačke su označene istim indeksom kao i tačka. Na primjer, izrazite radijus vektor i brzinu, respektivno k th point.

Na svaku tačku sistema djeluju sile dva porijekla: prvo, sile čiji izvori leže izvan sistema, tzv. vanjski snage i određen ; drugo, sile iz drugih tačaka datog sistema, tzv interni snage i određen . Unutrašnje sile zadovoljavaju treći Newtonov zakon. Razmotrimo najjednostavnija svojstva unutrašnjih sila koje djeluju na cijeli mehanički sistem u bilo kojem stanju.

Prva nekretnina. Geometrijski zbir svih unutrašnjih sila sistema (glavni vektor unutrašnjih sila) jednak je nuli.

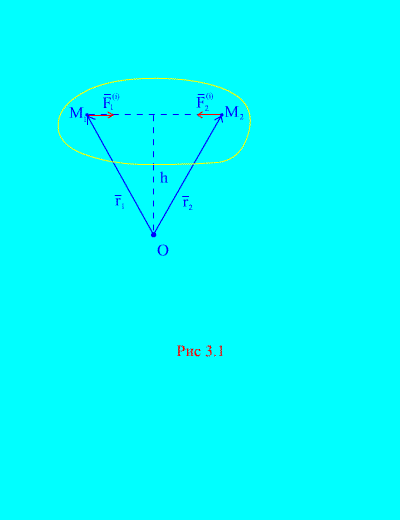
Zaista, ako uzmemo u obzir bilo koje dvije proizvoljne tačke sistema, na primjer i (Sl. 3.1), zatim za njih , jer sile akcije i reakcije su uvijek jednake po veličini, djelujući duž jedne linije djelovanja u suprotnom smjeru, koji povezuje tačke interakcije. Dakle, glavni vektor unutrašnjih sila čine parovi sila međudjelujućih tačaka

(3.1)

Druga nekretnina. Geometrijski zbir momenata svih unutrašnjih sila u odnosu na proizvoljnu tačku u prostoru jednak je nuli.

Razmotrimo sistem momenata sila u odnosu na tačku O(Sl. 3.1). Od (Sl. 3.1). to je jasno

,

jer obje sile imaju iste krakove i suprotne smjerove vektorskih momenata. Glavni moment unutrašnjih sila u odnosu na tačku O sastoji se od vektorske sume takvih izraza i jednaka je nuli. dakle,

Neka vanjske i unutrašnje sile djeluju na mehanički sistem koji se sastoji od N bodova (Sl. 3.2). Ako se rezultanta vanjskih sila i rezultanta svih unutrašnjih sila primjenjuju na svaku tačku sistema, tada za bilo koju k U tački sistema mogu se sastaviti diferencijalne jednačine kretanja. Biće ukupno takvih jednačina N:

i u projekcijama na fiksne koordinatne ose 3 N:

(3.4)

Vektorske jednačine (3.3) ili ekvivalentne skalarne jednačine (3.4) predstavljaju diferencijalne zakone kretanja materijalnih tačaka čitavog sistema. Ako se sve tačke kreću paralelno s jednom ravninom ili jednom pravom linijom, tada će broj jednačina (3.4) u prvom slučaju biti 2 N, u drugom N.

Primjer 1. Dvije mase su međusobno povezane nerastezljivim kablom prebačenim preko bloka (Sl. 3.3). Zanemarujući sile trenja, kao i masu bloka i sajle, određuju se zakon kretanja tereta i napetost kabla.

Rješenje. Sistem se sastoji od dva materijalna tijela (povezana nerastavljivim kablom) koja se kreću paralelno s istom osom X. Zapišimo diferencijalne zakone kretanja u projekcijama na osu X za svako telo.

Neka desni uteg pada sa ubrzanjem, a zatim će leva težina rasti sa ubrzanjem. Mentalno se oslobađamo veze (kabla) i zamjenjujemo je reakcijama i (Sl. 3.3). S obzirom da su tijela slobodna, nacrtajmo diferencijalne zakone kretanja u projekciji na osu X(što znači da su napetosti navoja unutrašnje sile, a težina opterećenja vanjske):

Pošto i (tela su povezana nerastezljivim kablom), dobijamo

Rješavanje ovih jednačina za ubrzanje i napetost kabla T, dobijamo

.

Imajte na umu da napetost u kablu nije jednaka sili gravitacije odgovarajućeg opterećenja.

3. 2. Teorema o kretanju centra masa

Poznato je da se kruto tijelo i mehanički sistem u ravni mogu kretati prilično složeno. Do prve teoreme o kretanju tijela i mehaničkog sistema može se doći na sljedeći način: baciti k.-l. predmet koji se sastoji od mnogo čvrstih tijela spojenih zajedno. Jasno je da će letjeti u paraboli. Ovo je otkriveno prilikom proučavanja kretanja tačke. Međutim, sada objekat nije tačka. Okreće se i njiše tokom leta oko određenog efektivnog centra koji se kreće po paraboli. Prva teorema o kretanju složenih objekata kaže da je određeni efektivni centar centar mase pokretnog objekta. Centar mase nije nužno lociran u samom tijelu;

Teorema. Centar mase mehaničkog sistema kreće se kao materijalna tačka sa masom jednakom masi celog sistema, na koju se primenjuju sve spoljne sile koje deluju na sistem.

Da bismo dokazali teoremu, prepisujemo diferencijalne zakone kretanja (3.3) u sljedećem obliku:

(3.5)

Gdje N – broj sistemskih poena.

Dodajmo jednačine pojam po član:

(A)

Položaj centra mase mehaničkog sistema u odnosu na odabrani koordinatni sistem određuje se formulom (2.1): Gdje M– masa sistema. Tada će biti zapisana lijeva strana jednakosti (a).

Prvi zbir na desnoj strani jednakosti (a) jednak je glavnom vektoru vanjskih sila, a posljednji, po svojstvu unutrašnjih sila, jednak je nuli. Tada će jednakost (a), uzimajući u obzir (b), biti prepisana

, (3.6)

one. proizvod mase sistema i ubrzanja centra njegove mase jednak je geometrijskom zbiru svih vanjskih sila koje djeluju na sistem.

Iz jednačine (3.6) proizilazi da unutrašnje sile ne utiču direktno na kretanje centra mase. Međutim, u nekim slučajevima oni su uzrok pojave vanjskih sila koje djeluju na sistem. Dakle, unutrašnje sile koje pokreću pogonske točkove automobila u rotaciju uzrokuju da vanjska sila prianjanja primijenjena na naplatak kotača djeluje na njega.

Primjer 2. Mehanizam, smješten u okomitoj ravnini, postavljen je na horizontalnu glatku ravninu i pričvršćen na nju šipkama čvrsto pričvršćenim na površinu TO I L (Sl. 3.4).

Radijus diska 1 R nepomičan. Disk 2 masa m i radijus r pričvršćena na polugu, dužina R+ r u tački C 2. Ručica se stalno okreće

ugaona brzina. U početnom trenutku, radilica je zauzela desni horizontalni položaj. Zanemarujući masu radilice, odredite maksimalne horizontalne i vertikalne sile koje djeluju na šipke ako je ukupna masa okvira i točka 1 jednaka M. Uzmite u obzir i ponašanje mehanizma u odsustvu šipki.

Rješenje. Sistem se sastoji od dvije mase ( N=2 ): fiksni disk 1 sa okvirom i pokretni disk 2. Usmjerite osovinu at kroz težište nepokretnog diska okomito prema gore, os X– duž horizontalne ravni.

Zapišimo teoremu o kretanju centra mase (3.6) u koordinatnom obliku

Vanjske sile ovog sistema su: težina okvira i fiksnog diska - Mg, težina pokretnog diska – mg, - ukupna horizontalna reakcija vijaka, - normalna ukupna reakcija ravnine. dakle,

Tada će zakoni kretanja (b) biti prepisani

Izračunajmo koordinate centra mase mehaničkog sistema:

; (G)

kao što se vidi iz (Sl. 3.4), , , (ugao poluge), . Zamjena ovih izraza u (d) i izračunavanje drugih izvoda s obzirom na vrijeme t iz , , to smo dobili

(d)

Zamjenom (c) i (e) u (b), nalazimo

Horizontalni pritisak koji djeluje na šipke je najveći i najmanji kada cos = 1 shodno tome, tj.

Pritisak mehanizma na horizontalnoj ravni ima najveću i najnižu vrijednost kada grijeh shodno tome, tj.

Zapravo, prvi problem dinamike je riješen: prema poznatim jednačinama kretanja centra mase sistema (d), sile uključene u kretanje se obnavljaju.

U nedostatku rešetki K I L (Sl. 3.4), mehanizam može početi da poskakuje iznad horizontalne ravni. To će se dogoditi kada, tj. kada , slijedi da kutna brzina rotacije radilice, pri kojoj mehanizam odskače, mora zadovoljiti jednakost

.

3. 3. Zakon održanja kretanja centra masa

Ako je glavni vektor vanjskih sila koje djeluju na sistem jednak nuli, tj. , zatim od(3.6)slijedi da je ubrzanje centra mase nula, dakle, brzina centra mase je konstantna po veličini i smjeru. Ako, konkretno, u početnom trenutku centar mase miruje, onda miruje cijelo vrijeme dok je glavni vektor vanjskih sila jednak nuli.

Iz ove teoreme slijedi nekoliko posljedica.

· Unutrašnje sile same po sebi ne mogu promijeniti prirodu kretanja centra mase sistema.

· Ako je glavni vektor vanjskih sila koje djeluju na sistem jednak nuli, tada centar mase miruje ili se kreće ravnomjerno i pravolinijski.

· Ako je projekcija glavnog vektora vanjskih sila sistema na neku fiksnu osu jednaka nuli, tada se projekcija brzine centra mase sistema na ovu osu ne mijenja.

· Par sila primijenjen na kruto tijelo ne može promijeniti kretanje njegovog centra mase (može samo uzrokovati rotaciju tijela oko centra mase).

Razmotrimo primjer koji ilustruje zakon održanja kretanja centra mase.

Primjer 3. Dvije mase su povezane nerastezljivom niti bačenom kroz blok (Sl. 3.5), fiksiran na klin sa masom M. Klin se oslanja na glatku horizontalnu ravan. U početnom trenutku sistem je mirovao. Pronađite pomak klina duž ravnine kada se prvi teret spusti na visinu N. Zanemarite masu bloka i konca.

Rješenje. Vanjske sile koje djeluju na klin zajedno sa opterećenjima su gravitacija i Mg, kao i normalna reakcija glatke horizontalne površine N. Posljedično,

Pošto je u početnom trenutku sistem mirovao, imamo .

Izračunajmo koordinate centra mase sistema u i trenutno t 1 kada teret teži gće se spustiti na visinu H.

Za trenutak:

,

Gdje , , X– koordinate centra mase tereta težine g, g i klina težine Mg.

Pretpostavimo da se klin u trenutku pomiče u pozitivnom smjeru ose Ox po iznosu L, ako težina tereta padne na visinu N. Onda, za trenutak

jer tereti zajedno sa klinom će se pomeriti L udesno, a teret će se kretati prema gore duž klina. Budući da , onda nakon proračuna dobivamo

.

3.4. Količina pokreta sistema

3.4.1. Proračun impulsa sistema

Zamah materijalne tačke je vektorska veličina jednaka proizvodu mase tačke i njenog vektora brzine

Jedinica mjerenja momenta -

Impuls mehaničkog sistema je vektorski zbir impulsa pojedinih tačaka sistema, tj.

Gdje N – broj sistemskih poena.

Zamah mehaničkog sistema može se izraziti u smislu mase sistema M i brzinu centra mase. stvarno,

one. Impuls sistema jednak je proizvodu mase čitavog sistema i brzine njegovog centra mase. Smjer je isti kao i smjer (Sl. 3.6)

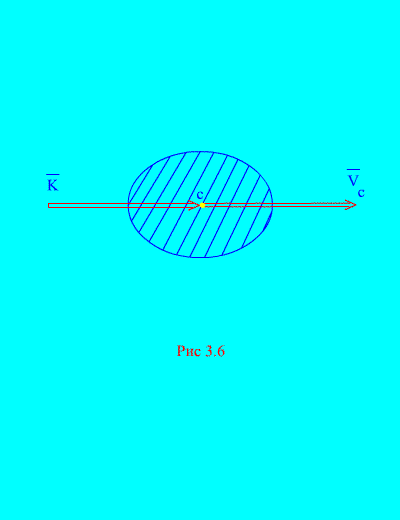
U projekcijama na pravougaone ose imamo

gdje su , , projekcije brzine centra mase sistema.

Evo M– masa mehaničkog sistema; se ne mijenja kada se sistem pomjeri.

Ovi rezultati su posebno pogodni za korištenje pri izračunavanju količina kretanja krutih tijela.

Iz formule (3.7) je jasno da ako se mehanički sistem kreće tako da njegovo središte mase ostaje nepomično, onda impuls sistema ostaje jednak nuli.

3.4.2. Elementarni impuls pune snage

Djelovanje sile na materijalnu tačku tokom vremena dt može se okarakterisati elementarnim impulsom. Ukupni impuls sile tokom vremena t, ili impuls sile, određen formulom

ili u projekcijama na koordinate osi

(3.8a)

Jedinica impulsa sile je .

3.4.3. Teorema o promjeni impulsa sistema

Neka spoljne i unutrašnje sile budu primenjene na tačke sistema. Tada za svaku tačku sistema možemo primijeniti diferencijalne zakone kretanja (3.3), imajući na umu da :

.

Sumirajući sve tačke sistema, dobijamo

Po svojstvu unutrašnjih sila i po definiciji imamo

(3.9)

Množenjem obje strane ove jednačine sa dt, dobijamo teoremu o promjeni impulsa u diferencijalnom obliku:

, (3.10)

one. diferencijalni impuls mehaničkog sistema jednak je vektorskom zbiru elementarnih impulsa svih vanjskih sila koje djeluju na tačke mehaničkog sistema.

Izračunavanje integrala obe strane (3.10) tokom vremena od 0 do t, dobijamo teoremu u konačnom ili integralnom obliku

(3.11)

U projekcijama na koordinatne ose ćemo imati

Promjena impulsa mehaničkog sistema tokom vremenat, jednak je vektorskom zbiru svih impulsa vanjskih sila koje djeluju na tačke mehaničkog sistema u isto vrijeme.

Primjer 4. Težina opterećenja m spušta se niz nagnutu ravan iz mirovanja pod uticajem sile F, proporcionalno vremenu: , gdje (Sl. 3.7). Koju će brzinu tijelo postići nakon toga t sekundi nakon početka kretanja, ako je koeficijent trenja klizanja tereta na kosoj ravni jednak f.

Rješenje. Hajde da opišemo sile koje se primenjuju na opterećenje: mg – sila gravitacije opterećenja, N je normalna reakcija ravnine, je sila trenja klizanja tereta na ravni, i . Smjer svih sila je prikazan u (Sl. 3.7).

Usmjerimo osu X duž nagnute ravni prema dolje. Napišimo teoremu o promjeni impulsa (3.11) u projekciji na osu X:

(A)

Prema stanju, jer u početnom trenutku je opterećenje bilo u mirovanju. Zbir projekcija impulsa svih sila na x osu je jednak

dakle,

,

.

3.4.4. Zakoni održanja impulsa

Zakoni održanja su dobijeni kao posebni slučajevi teoreme o promjeni impulsa. Moguća su dva posebna slučaja.

· Ako je vektorski zbir svih vanjskih sila primijenjenih na sistem jednak nuli, tj. , onda iz teoreme slijedi (3.9) , Šta ,

one. ako je glavni vektor vanjskih sila sistema nula, tada je količina kretanja sistema konstantna po veličini i smjeru.

· Ako je projekcija glavnog vektora vanjskih sila na bilo koju koordinatnu osu jednaka nuli, na primjer Ox, tj. , tada je projekcija impulsa na ovu osu konstantna vrijednost.

Razmotrimo primjer primjene zakona održanja impulsa.

Primjer 5. Balističko klatno je tijelo s masom okačenom na dugačku nit (Sl. 3.8).

Metak mase koji se kreće brzinom V i udarivši u nepokretno tijelo, zaglavi se u njemu i tijelo skrene. Kolika je bila brzina metka ako se tijelo podiglo na visinu h ?

Rješenje. Neka tijelo sa zaglavljenim metkom dobije brzinu. Zatim, koristeći zakon održanja količine kretanja tokom interakcije dvaju tijela, možemo pisati .

Brzina se može izračunati korištenjem zakona održanja mehaničke energije . Onda . Kao rezultat nalazimo

.

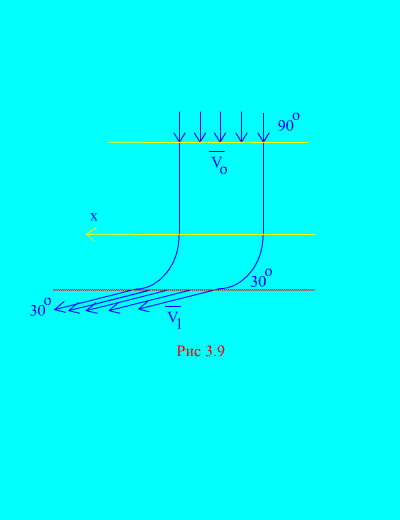
Primjer 6. Voda ulazi u stacionarni kanal (Sl. 3.9) varijabilni poprečni presjek sa brzinom pod uglom u odnosu na horizontalu; površina poprečnog presjeka kanala na ulazu; brzina vode na izlazu iz kanala čini ugao sa horizontom.

Odredite horizontalnu komponentu reakcije koju voda ima na zidovima kanala. Gustina vode .

Rješenje. Odredit ćemo horizontalnu komponentu reakcije koju vrše zidovi kanala na vodu. Ova sila je jednaka po veličini i suprotnog predznaka od željene sile. Imamo, prema (3.11a),

. (A)

Izračunavamo masu zapremine tečnosti koja ulazi u kanal za vreme t:

Poziva se vrijednost rAV 0 druga masa - masa tekućine koja teče kroz bilo koji dio cijevi u jedinici vremena.

Ista količina vode izlazi iz kanala u isto vrijeme. Početna i krajnja brzina su date u uslovu.

Izračunajmo desnu stranu jednakosti (a), koja određuje zbir projekcija na horizontalnu osu vanjskih sila koje djeluju na sistem (vodu). Jedina horizontalna sila je horizontalna komponenta rezultujuće zidne reakcije Rx. Ova sila je konstantna tokom stabilnog kretanja vode. Zbog toga

. (V)

Zamenivši (b) i (c) u (a), dobijamo

3.5. Kinetički moment sistema

3.5.1. Glavni moment impulsa sistema

Neka je radijus vektor tačke sa masom sistema u odnosu na neku tačku A, koja se zove centar (Sl. 3.10).

Moment momenta (kinetički moment) tačke u odnosu na centar A zove se vektor , određena formulom

. (3.12)

U ovom slučaju, vektor usmjeren okomito na ravan koja prolazi kroz centar A i vektor .

Moment momenta (kinetički moment) tačke u odnosu na osu naziva se projekcija momenta momenta momenta tačke na ovu osu u odnosu na bilo koji centar odabran na ovoj osi.

Glavni moment momenta (kinetički moment) sistema u odnosu na centar A naziva se količina

(3.13)

Glavni moment momenta (kinetički moment) sistema u odnosu na osu naziva se projekcija na ovu osu glavnog momenta momenta gibanja sistema u odnosu na bilo koji odabran na ovoj središnja os.

3.5.2. Kinetički moment rotirajućeg krutog tijela oko ose rotacije

Poravnajmo fiksnu tačku O tijelo koje leži na osi rotacije Oz, sa ishodištem koordinatnog sistema Ohooz, čije će se ose rotirati zajedno sa tijelom (Sl. 3.11). Neka je radijus vektor točke tijela u odnosu na početak koordinata njegova projekcija na os će biti označena sa , , . Projekcije vektora ugaone brzine tela na iste ose označavamo kao 0, 0, ().

Ministarstvo obrazovanja i nauke Ruske Federacije

Federalna državna budžetska obrazovna ustanova visokog stručnog obrazovanja

"Kubanski državni tehnološki univerzitet"

Teorijska mehanika

Dio 2 dinamika

Odobreno od strane Uredničke i izdavačke komisije

univerzitetsko vijeće kao

nastavno pomagalo

Krasnodar

UDK 531.1/3 (075)

Teorijska mehanika. Dio 2. Dinamika: Udžbenik / L.I. Kuban. stanje technol.un-t. Krasnodar, 2011. 123 str.

ISBN 5-230-06865-5

Teorijski materijal je predstavljen u kratkom obliku, dati su primjeri rješavanja problema, od kojih većina odražava stvarna tehnička pitanja, a pažnja je posvećena izboru racionalne metode rješenja.

Dizajniran za prvostupnike dopisnog i učenja na daljinu u građevinarstvu, saobraćaju i mašinstvu.

Table 1 Ill. 68 Bibliografija 20 naslova

Naučni urednik Kandidat tehničkih nauka, vanredni profesor. V.F.Melnikov

Recenzenti: šef Katedre za teorijsku mehaniku i teoriju mehanizama i mašina Kubanskog agrarnog univerziteta prof. F.M. Kanarev; Vanredni profesor Katedre za teorijsku mehaniku Kubanskog državnog tehnološkog univerziteta M.E. Multykh

Objavljeno odlukom Uredničkog i izdavačkog saveta Kubanskog državnog tehnološkog univerziteta.

Ponovno izdanje

ISBN 5-230-06865-5 KubSTU 1998

Predgovor

Ovaj udžbenik je namenjen vanrednim studentima građevinarstva, saobraćaja i mašinstva, ali se može koristiti za izučavanje dela „Dinamika“ kursa teorijske mehanike od strane vanrednih studenata drugih specijalnosti, kao i redovnih studenata. radeći samostalno.

Priručnik je sastavljen u skladu sa važećim nastavnim planom i programom predmeta teorijske mehanike i pokriva sva pitanja glavnog dijela predmeta. Svaki dio sadrži kratak teorijski materijal, praćen ilustracijama i metodološkim preporukama za njegovu upotrebu u rješavanju problema. Priručnik sadrži rješenja za 30 zadataka koji odražavaju stvarna tehnička pitanja i odgovaraju testnim zadacima za samostalno rješavanje. Za svaki problem je prikazan proračunski dijagram koji jasno ilustruje rješenje. Oblikovanje rješenja zadovoljava zahtjeve za formatiranje testnih radova za vanredne studente.

Autor izražava duboku zahvalnost nastavnicima Katedre za teorijsku mehaniku i teoriju mehanizama i mašina Kubanskog agrarnog univerziteta na njihovom velikom trudu u recenziji udžbenika, kao i nastavnicima Katedre za teorijsku mehaniku Kubanskog državnog tehnološkog univerziteta. Univerzitetu za vrijedne komentare i savjete o pripremi udžbenika za objavljivanje.

Sve kritičke komentare i sugestije autor će ubuduće prihvatati sa zahvalnošću.

Uvod

Dinamika je najvažniji dio teorijske mehanike. Većina specifičnih problema sa kojima se susreće u inženjerskoj praksi odnosi se na dinamiku. Koristeći zaključke statike i kinematike, dinamika uspostavlja opšte zakone kretanja materijalnih tela pod dejstvom primenjenih sila.

Najjednostavniji materijalni objekat je materijalna tačka. Materijalno tijelo bilo kojeg oblika može se uzeti kao materijalna tačka čije se dimenzije mogu zanemariti u problemu koji se razmatra. Tijelo konačnih dimenzija može se uzeti kao materijalna tačka ako razlika u kretanju njegovih tačaka nije značajna za dati problem. To se događa kada su dimenzije tijela male u odnosu na udaljenosti koje pokrivaju tačke tijela. Svaka čestica čvrstog tijela može se smatrati materijalnom tačkom.

Sile koje se primjenjuju na tačku ili materijalno tijelo dinamički se procjenjuju po njihovom dinamičkom utjecaju, odnosno po tome kako mijenjaju karakteristike kretanja materijalnih objekata.

Kretanje materijalnih objekata tokom vremena događa se u prostoru u odnosu na određeni referentni okvir. U klasičnoj mehanici, zasnovanoj na Newtonovim aksiomima, prostor se smatra trodimenzionalnim, njegova svojstva ne zavise od materijalnih objekata koji se kreću u njemu. Položaj tačke u takvom prostoru određen je sa tri koordinate. Vrijeme nije vezano za prostor i kretanje materijalnih objekata. Smatra se istim za sve referentne sisteme.

Zakoni dinamike opisuju kretanje materijalnih objekata u odnosu na apsolutne koordinatne ose, koje se konvencionalno prihvataju kao stacionarne. Za početak apsolutnog koordinatnog sistema uzima se da je centar Sunca, a ose su usmerene ka udaljenim, uslovno stacionarnim zvezdama. Prilikom rješavanja mnogih tehničkih problema, koordinatne ose povezane sa Zemljom mogu se smatrati uslovno nepokretnim.

Parametri mehaničkog kretanja materijalnih objekata u dinamici utvrđuju se matematičkim izvodima iz osnovnih zakona klasične mehanike.

Prvi zakon (zakon inercije):

Materijalna tačka održava stanje mirovanja ili ravnomernog i linearnog kretanja sve dok je dejstvom nekih sila ne izvuče iz tog stanja.

Ravnomerno i linearno kretanje tačke naziva se kretanje po inerciji. Mirovanje je poseban slučaj kretanja po inerciji, kada je brzina tačke nula.

Svaka materijalna tačka ima inerciju, odnosno nastoji da održi stanje mirovanja ili ravnomernog linearnog kretanja. Referentni sistem u odnosu na koji važi zakon inercije naziva se inercijalni, a kretanje posmatrano u odnosu na ovaj sistem naziva se apsolutnim. Svaki referentni sistem koji vrši translaciono pravolinijsko i ravnomerno kretanje u odnosu na inercijalni sistem takođe će biti inercijalni sistem.

Drugi zakon (osnovni zakon dinamike):

Ubrzanje materijalne tačke u odnosu na inercijski referentni sistem proporcionalno je sili primijenjenoj na tačku i poklapa se sa silom u smjeru:
.

Iz osnovnog zakona dinamike proizlazi da sa silom
ubrzanje
. Masa tačke karakteriše stepen otpora tačke na promene njene brzine, odnosno ona je mera inercije materijalne tačke.

Treći zakon (Zakon akcije i reakcije):

Sile kojima dva tijela djeluju jedno na drugo jednake su po veličini i usmjerene duž jedne prave u suprotnim smjerovima.

Sile koje se nazivaju akcija i reakcija primjenjuju se na različita tijela i stoga ne formiraju uravnotežen sistem.

Četvrti zakon (zakon o nezavisnosti snaga):

Uz istovremeno djelovanje više sila, ubrzanje materijalne točke jednako je geometrijskom zbroju ubrzanja koje bi tačka imala pod djelovanjem svake sile posebno:

, Gdje
,
,…,
.

Vrlo često je moguće identifikovati važne karakteristike kretanja mehaničkog sistema bez pribjegavanja integraciji sistema diferencijalnih jednačina kretanja. To se postiže primjenom općih teorema dinamike.

5.1. Osnovni pojmovi i definicije

Vanjske i unutrašnje sile. Svaka sila koja djeluje na tačku u mehaničkom sistemu je nužno ili aktivna sila ili reakcija spajanja. Čitav skup sila koje djeluju na tačke sistema može se različito podijeliti u dvije klase: vanjske sile i unutrašnje sile (indeksi e i i - od latinskih riječi externus - vanjski i internus - unutrašnji). Vanjske sile su one koje djeluju na tačke sistema iz tačaka i tijela koja nisu dio sistema koji se razmatra. Sile interakcije između tačaka i tijela sistema koji se razmatra nazivaju se unutrašnjim.

Ova podjela zavisi od toga koje materijalne tačke i tijela su uključene od strane istraživača u mehanički sistem koji se razmatra. Ako proširite sastav sistema uključivanjem dodatnih tačaka i tijela, tada neke sile koje su bile vanjske za prethodni sistem mogu postati unutrašnje za prošireni sistem.

Svojstva unutrašnjih sila. Pošto su ove sile sile interakcije između delova sistema, one ulaze u kompletan sistem unutrašnjih sila u „dvojke“, organizovane u skladu sa aksiomom akcija-reakcija. Svaka takva „dvojka“ ima prednosti

glavni vektor i glavni moment oko proizvoljnog centra jednaki su nuli. Pošto se kompletan sistem unutrašnjih sila sastoji samo od „dvojke“, onda

1) glavni vektor sistema unutrašnjih sila je nula,

2) glavni moment sistema unutrašnjih sila u odnosu na proizvoljnu tačku jednak je nuli.

Masa sistema je aritmetički zbir masa mk svih tačaka i tela koja čine sistem:

Centar mase(centar inercije) mehaničkog sistema je geometrijska tačka C čiji su vektor radijusa i koordinate određene formulama

gdje su radijus vektori i koordinate tačaka koje čine sistem.

Za kruto tijelo smješteno u jednoličnom gravitacijskom polju, položaji centra mase i centra gravitacije se poklapaju u drugim slučajevima, to su različite geometrijske točke;

Zajedno sa inercijskim referentnim sistemom, neinercijalni referentni sistem koji se kreće translativno često se razmatra istovremeno. Njegove koordinatne ose (Königove ose) biraju se tako da se ishodište C stalno poklapa sa centrom mase mehaničkog sistema. U skladu sa definicijom, centar mase je nepomičan u Koenigovim osama i nalazi se na početku koordinata.

Moment inercije sistema u odnosu na osu je skalarna veličina jednaka zbroju proizvoda masa mk svih tačaka sistema kvadratima njihovih udaljenosti do ose:

Ako je mehanički sistem kruto tijelo, da biste pronašli 12 možete koristiti formulu

gdje je gustina, zapremina koju tijelo zauzima.