एक्स 2 वाई 3एक्स 1 ग्राफ। मॉड्यूल के साथ ग्राफ़ परिवर्तन

1. भिन्नात्मक रैखिक फलन और उसका ग्राफ

y = P(x) / Q(x) के रूप का एक फलन, जहां P(x) और Q(x) बहुपद हैं, भिन्नात्मक परिमेय फलन कहलाता है।

अवधारणा के साथ भिन्नात्मक संख्याएंआप संभवतः एक-दूसरे को पहले से ही जानते हैं। वैसे ही तर्कसंगत कार्यऐसे फलन हैं जिन्हें दो बहुपदों के भागफल के रूप में दर्शाया जा सकता है।

यदि एक भिन्नात्मक परिमेय फलन दो का भागफल है रैखिक कार्य- प्रथम डिग्री के बहुपद, अर्थात्। प्रपत्र का कार्य

y = (ax + b) / (cx + d), तो इसे भिन्नात्मक रैखिक कहा जाता है।

ध्यान दें कि फ़ंक्शन में y = (ax + b) / (cx + d), c ≠ 0 (अन्यथा फ़ंक्शन रैखिक y = ax/d + b/d हो जाता है) और a/c ≠ b/d (अन्यथा फ़ंक्शन स्थिर है)। भिन्नात्मक रैखिक फलन सभी के लिए परिभाषित है वास्तविक संख्या, x = -d/c को छोड़कर। भिन्नात्मक रैखिक फलनों के ग्राफ़ उस ग्राफ़ y = 1/x से आकार में भिन्न नहीं होते हैं जिसे आप जानते हैं। एक वक्र जो फलन y = 1/x का ग्राफ है, कहलाता है अतिशयोक्ति. निरपेक्ष मान में x में असीमित वृद्धि के साथ, फ़ंक्शन y = 1/x निरपेक्ष मान में असीमित रूप से घटता है और ग्राफ़ की दोनों शाखाएं भुज तक पहुंचती हैं: दाईं ओर ऊपर से पहुंचती है, और बाईं ओर नीचे से। हाइपरबोला की शाखाएँ जिस रेखा तक पहुँचती हैं, उसे उसकी रेखाएँ कहा जाता है स्पर्शोन्मुख.

उदाहरण 1।

y = (2x + 1) / (x – 3).

समाधान।

आइए पूरे भाग का चयन करें: (2x + 1) / (x – 3) = 2 + 7/(x – 3)।

अब यह देखना आसान है कि इस फ़ंक्शन का ग्राफ़ निम्नलिखित परिवर्तनों द्वारा फ़ंक्शन y = 1/x के ग्राफ़ से प्राप्त किया गया है: 3 इकाई खंडों द्वारा दाईं ओर शिफ्ट, ओए अक्ष के साथ 7 बार खींचना और 2 द्वारा शिफ्ट करना इकाई खंड ऊपर की ओर।

किसी भी अंश y = (ax + b) / (cx + d) को "पूर्णांक भाग" को हाइलाइट करते हुए, इसी तरह से लिखा जा सकता है। परिणामस्वरूप, सभी भिन्नात्मक रैखिक फलनों के ग्राफ़ अतिपरवलय हैं, विभिन्न तरीकों सेसमन्वय अक्षों के अनुदिश स्थानांतरित और ओए अक्ष के अनुदिश फैला हुआ।

किसी भी मनमाने ढंग से भिन्नात्मक-रैखिक फ़ंक्शन का ग्राफ़ बनाने के लिए, इस फ़ंक्शन को परिभाषित करने वाले भिन्न को बदलना बिल्कुल भी आवश्यक नहीं है। चूँकि हम जानते हैं कि ग्राफ़ एक अतिपरवलय है, इसलिए यह उन सीधी रेखाओं को खोजने के लिए पर्याप्त होगा जिन तक इसकी शाखाएँ पहुँचती हैं - अतिपरवलय x = -d/c और y = a/c के अनंतस्पर्शी।

उदाहरण 2.

फ़ंक्शन y = (3x + 5)/(2x + 2) के ग्राफ़ के स्पर्शोन्मुख खोजें।

समाधान।

x = -1 पर फ़ंक्शन परिभाषित नहीं है। इसका मतलब यह है कि सीधी रेखा x = -1 एक ऊर्ध्वाधर अनंतस्पर्शी के रूप में कार्य करती है। क्षैतिज अनंतस्पर्शी को खोजने के लिए, आइए जानें कि जब तर्क x निरपेक्ष मान में बढ़ता है तो फ़ंक्शन y(x) का मान क्या होता है।

ऐसा करने के लिए, भिन्न के अंश और हर को x से विभाजित करें:

y = (3 + 5/x) / (2 + 2/x).

x → ∞ के रूप में भिन्न की प्रवृत्ति 3/2 हो जाएगी। इसका मतलब यह है कि क्षैतिज अनंतस्पर्शी सीधी रेखा y = 3/2 है।

उदाहरण 3.

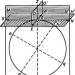
फ़ंक्शन y = (2x + 1)/(x + 1) को ग्राफ़ करें।

समाधान।

आइए भिन्न का "संपूर्ण भाग" चुनें:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

2 – 1/(x + 1).

अब यह देखना आसान है कि इस फ़ंक्शन का ग्राफ़ निम्नलिखित परिवर्तनों द्वारा फ़ंक्शन y = 1/x के ग्राफ़ से प्राप्त किया गया है: बाईं ओर 1 इकाई द्वारा बदलाव, ऑक्स के संबंध में एक सममित प्रदर्शन और द्वारा एक बदलाव ओए अक्ष के साथ ऊपर 2 इकाई खंड।

डोमेन D(y) = (-∞; -1)ᴗ(-1; +∞).

मानों की सीमा E(y) = (-∞; 2)ᴗ(2; +∞).

अक्षों के साथ प्रतिच्छेदन बिंदु: c Oy: (0; 1); सी बैल: (-1/2; 0). परिभाषा के क्षेत्र के प्रत्येक अंतराल पर फ़ंक्शन बढ़ता है।

उत्तर: चित्र 1.

2. भिन्नात्मक तर्कसंगत कार्य

y = P(x) / Q(x) के रूप के भिन्नात्मक परिमेय फलन पर विचार करें, जहां P(x) और Q(x) पहले से अधिक घात वाले बहुपद हैं।

ऐसे तर्कसंगत कार्यों के उदाहरण:

y = (x 3 – 5x + 6) / (x 7 – 6) या y = (x – 2) 2 (x + 1) / (x 2 + 3)।

यदि फ़ंक्शन y = P(x) / Q(x) पहले से अधिक डिग्री वाले दो बहुपदों के भागफल का प्रतिनिधित्व करता है, तो इसका ग्राफ, एक नियम के रूप में, अधिक जटिल होगा, और कभी-कभी इसे सटीक रूप से बनाना मुश्किल हो सकता है। , सभी विवरणों के साथ। हालाँकि, अक्सर उन तकनीकों के समान उपयोग करना पर्याप्त होता है जिन्हें हम पहले ही ऊपर प्रस्तुत कर चुके हैं।

माना कि भिन्न एक उचित भिन्न है (n< m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:

P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+

एल 1 /(एक्स – के एस) एमएस + एल 2 /(एक्स – के एस) एमएस-1 + … + एल एमएस /(एक्स – के एस) + …+

+ (बी 1 एक्स + सी 1) / (एक्स 2 +पी 1 एक्स + क्यू 1) एम1 + … + (बी एम1 एक्स + सी एम1) / (एक्स 2 +पी 1 एक्स + क्यू 1) + …+

+ (एम 1 एक्स + एन 1) / (एक्स 2 +पी टी एक्स + क्यू टी) एम1 + … + (एम एम1 एक्स + एन एम1) / (एक्स 2 +पी टी एक्स + क्यू टी)।

जाहिर है, भिन्नात्मक परिमेय फलन का ग्राफ प्राथमिक भिन्नों के ग्राफ के योग के रूप में प्राप्त किया जा सकता है।

भिन्नात्मक परिमेय फलनों का रेखांकन आलेखित करना

आइए भिन्नात्मक परिमेय फलन के ग्राफ़ बनाने के कई तरीकों पर विचार करें।

उदाहरण 4.

फ़ंक्शन y = 1/x 2 का ग्राफ़ बनाएं।

समाधान।

हम y = 1/x 2 का ग्राफ बनाने के लिए फ़ंक्शन y = x 2 के ग्राफ का उपयोग करते हैं और ग्राफ़ को "विभाजित" करने की तकनीक का उपयोग करते हैं।

डोमेन D(y) = (-∞; 0)ᴗ(0; +∞).

मानों की सीमा E(y) = (0; +∞).

अक्षों के साथ प्रतिच्छेदन का कोई बिंदु नहीं है। फ़ंक्शन सम है. अंतराल (-∞; 0) से सभी x के लिए बढ़ता है, x के लिए 0 से +∞ तक घटता है।

उत्तर: चित्र 2.

उदाहरण 5.

फ़ंक्शन y = (x 2 – 4x + 3) / (9 – 3x) का ग्राफ़ बनाएं।

समाधान।

डोमेन D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/ 3 + 1/3.

यहां हमने एक रैखिक फलन में गुणनखंडन, न्यूनीकरण और न्यूनीकरण की तकनीक का उपयोग किया।

उत्तर: चित्र 3.

उदाहरण 6.

फ़ंक्शन y = (x 2 – 1)/(x 2 + 1) का ग्राफ़ बनाएं।

समाधान।

परिभाषा का क्षेत्र D(y) = R है। चूँकि फलन सम है, ग्राफ़ कोटि के बारे में सममित है। ग्राफ़ बनाने से पहले, आइए अभिव्यक्ति को फिर से रूपांतरित करें, पूरे भाग पर प्रकाश डालें:

y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1).

ध्यान दें कि भिन्नात्मक परिमेय फलन के सूत्र में पूर्णांक भाग को अलग करना ग्राफ़ बनाते समय मुख्य कार्यों में से एक है।

यदि x → ±∞, तो y → 1, अर्थात। सीधी रेखा y = 1 एक क्षैतिज अनंतस्पर्शी है।

उत्तर: चित्र 4.

उदाहरण 7.

आइए फ़ंक्शन y = x/(x 2 + 1) पर विचार करें और इसका सबसे बड़ा मान सटीक रूप से खोजने का प्रयास करें, अर्थात। सबसे उच्च बिंदुग्राफ़ का दाहिना आधा भाग. इस ग्राफ़ को सटीक रूप से बनाने के लिए आज का ज्ञान पर्याप्त नहीं है। जाहिर है, हमारा वक्र बहुत ऊंचा "उठ" नहीं सकता, क्योंकि हर तेजी से अंश से आगे निकलना शुरू कर देता है। आइए देखें कि क्या फ़ंक्शन का मान 1 के बराबर हो सकता है। ऐसा करने के लिए, हमें समीकरण x 2 + 1 = x, x 2 – x + 1 = 0 को हल करना होगा। इस समीकरण की कोई वास्तविक जड़ें नहीं हैं। इसका मतलब है कि हमारी धारणा ग़लत है. सबसे अधिक खोजने के लिए बडा महत्वफ़ंक्शन, आपको यह पता लगाना होगा कि समीकरण A = x/(x 2 + 1) का सबसे बड़ा A क्या समाधान होगा। आइए मूल समीकरण को एक द्विघात समीकरण से बदलें: Аx 2 – x + А = 0. इस समीकरण का एक हल है जब 1 – 4А 2 ≥ 0. यहां से हम पाते हैं उच्चतम मूल्यए = 1/2.

उत्तर: चित्र 5, अधिकतम y(x) = ½।

क्या आपके पास अभी भी प्रश्न हैं? क्या आप नहीं जानते कि फ़ंक्शंस का ग्राफ़ कैसे बनाया जाता है?
किसी ट्यूटर से सहायता प्राप्त करने के लिए -.
पहला पाठ निःशुल्क है!

ब्लॉग.साइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, मूल स्रोत के लिंक की आवश्यकता होती है।

मॉड्यूल वाले फ़ंक्शंस के ग्राफ़ का निर्माण आमतौर पर स्कूली बच्चों के लिए काफी कठिनाइयों का कारण बनता है। हालाँकि, सब कुछ इतना बुरा नहीं है। ऐसी समस्याओं को हल करने के लिए कुछ एल्गोरिदम को याद रखना पर्याप्त है, और आप सबसे प्रतीत होने वाले के लिए भी आसानी से एक ग्राफ बना सकते हैं जटिल कार्य. आइए जानें कि ये किस प्रकार के एल्गोरिदम हैं।

1. फ़ंक्शन y = |f(x)| का ग्राफ़ प्लॉट करना

ध्यान दें कि फ़ंक्शन मानों का सेट y = |f(x)| : y ≥ 0. इस प्रकार, ऐसे कार्यों के ग्राफ़ हमेशा पूरी तरह से ऊपरी आधे तल में स्थित होते हैं।

फ़ंक्शन y = |f(x)| का ग्राफ प्लॉट करना इसमें निम्नलिखित सरल चार चरण शामिल हैं।

1) सावधानीपूर्वक और सावधानी से फ़ंक्शन y = f(x) का ग्राफ़ बनाएं।

2) ग्राफ़ पर 0x अक्ष के ऊपर या उस पर स्थित सभी बिंदुओं को अपरिवर्तित छोड़ दें।

3) ग्राफ़ के उस भाग को प्रदर्शित करें जो 0x अक्ष के नीचे स्थित है, 0x अक्ष के सापेक्ष सममित रूप से।

उदाहरण 1. फलन y = |x 2 – 4x + 3| का एक ग्राफ बनाएं

1) हम फ़ंक्शन y = x 2 – 4x + 3 का एक ग्राफ़ बनाते हैं। जाहिर है, इस फ़ंक्शन का ग्राफ़ एक परवलय है। आइए निर्देशांक अक्षों और परवलय के शीर्ष के निर्देशांक के साथ परवलय के प्रतिच्छेदन के सभी बिंदुओं के निर्देशांक ज्ञात करें।

एक्स 2 – 4एक्स + 3 = 0.

एक्स 1 = 3, एक्स 2 = 1.

इसलिए, परवलय 0x अक्ष को बिंदुओं (3, 0) और (1, 0) पर काटता है।

y = 0 2 – 4 0 + 3 = 3.

इसलिए, परवलय 0y अक्ष को बिंदु (0, 3) पर काटता है।

परवलय शीर्ष निर्देशांक:

x में = -(-4/2) = 2, y में = 2 2 – 4 2 + 3 = -1.

इसलिए, बिंदु (2, -1) इस परवलय का शीर्ष है।

प्राप्त आंकड़ों का उपयोग करके एक परवलय बनाएं (चित्र .1)

2) 0x अक्ष के नीचे स्थित ग्राफ़ का भाग 0x अक्ष के सापेक्ष सममित रूप से प्रदर्शित होता है।

3) हमें मूल फ़ंक्शन का एक ग्राफ़ मिलता है ( चावल। 2, बिंदीदार रेखा में दिखाया गया है)।

2. फ़ंक्शन प्लॉट करना y = f(|x|)

ध्यान दें कि फॉर्म y = f(|x|) के फ़ंक्शन सम हैं:

y(-x) = f(|-x|) = f(|x|) = y(x). इसका मतलब यह है कि ऐसे फ़ंक्शन के ग्राफ़ 0y अक्ष के बारे में सममित हैं।

फ़ंक्शन y = f(|x|) का ग्राफ़ प्लॉट करने में क्रियाओं की निम्नलिखित सरल श्रृंखला शामिल होती है।

1) फ़ंक्शन y = f(x) का ग्राफ़ बनाएं।

2) ग्राफ़ के उस भाग को छोड़ दें जिसके लिए x ≥ 0 है, अर्थात ग्राफ़ का वह भाग जो दाहिने आधे तल में स्थित है।

3) बिंदु (2) में निर्दिष्ट ग्राफ़ के भाग को 0y अक्ष पर सममित रूप से प्रदर्शित करें।

4) अंतिम ग्राफ़ के रूप में, बिंदु (2) और (3) में प्राप्त वक्रों के मिलन का चयन करें।

उदाहरण 2. फ़ंक्शन y = x 2 – 4 · |x| का एक ग्राफ बनाएं +3

चूँकि x 2 = |x| 2, तो मूल फ़ंक्शन को निम्नलिखित रूप में फिर से लिखा जा सकता है: y = |x| 2 – 4 · |x| +3. अब हम ऊपर प्रस्तावित एल्गोरिदम लागू कर सकते हैं।

1) हम सावधानीपूर्वक और सावधानीपूर्वक फ़ंक्शन y = x 2 – 4 x + 3 का ग्राफ़ बनाते हैं (यह भी देखें चावल। 1).

2) हम ग्राफ़ के उस भाग को छोड़ देते हैं जिसके लिए x ≥ 0 है, अर्थात ग्राफ़ का वह भाग जो दाहिने आधे तल में स्थित है।

3) ग्राफ़ के दाईं ओर को 0y अक्ष पर सममित रूप से प्रदर्शित करें।

(चित्र 3).

उदाहरण 3. फ़ंक्शन y = log 2 |x| का एक ग्राफ बनाएं

हम ऊपर दी गई योजना लागू करते हैं।

1) फ़ंक्शन y = log 2 x का एक ग्राफ़ बनाएं (चित्र 4).

3. फ़ंक्शन y = |f(|x|)| को प्लॉट करना

ध्यान दें कि फॉर्म y = |f(|x|)| के फ़ंक्शन सम भी हैं. दरअसल, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), और इसलिए, उनके ग्राफ़ 0y अक्ष के बारे में सममित हैं। ऐसे कार्यों के मूल्यों का सेट: y ≥ 0. इसका मतलब यह है कि ऐसे फ़ंक्शंस के ग्राफ़ पूरी तरह से ऊपरी आधे तल में स्थित हैं।

फ़ंक्शन y = |f(|x|)| को प्लॉट करने के लिए, आपको यह करना होगा:

1) फ़ंक्शन y = f(|x|) का सावधानीपूर्वक ग्राफ़ बनाएं।

2) ग्राफ़ के उस भाग को अपरिवर्तित छोड़ दें जो 0x अक्ष के ऊपर या पर है।

3) 0x अक्ष के नीचे स्थित ग्राफ़ के भाग को 0x अक्ष के सापेक्ष सममित रूप से प्रदर्शित करें।

4) अंतिम ग्राफ़ के रूप में, बिंदु (2) और (3) में प्राप्त वक्रों के मिलन का चयन करें।

उदाहरण 4. फ़ंक्शन y = |-x 2 + 2|x| का एक ग्राफ बनाएं – 1|.

1) ध्यान दें कि x 2 = |x| 2. इसका मतलब है कि मूल फ़ंक्शन के बजाय y = -x 2 + 2|x| - 1

आप फ़ंक्शन y = -|x| का उपयोग कर सकते हैं 2 + 2|x| – 1, चूँकि उनके ग्राफ़ मेल खाते हैं।

हम एक ग्राफ y = -|x| बनाते हैं 2 + 2|x| – 1. इसके लिए हम एल्गोरिथम 2 का उपयोग करते हैं।

ए) फ़ंक्शन y = -x 2 + 2x - 1 का ग्राफ़ बनाएं (चित्र 6).

बी) हम ग्राफ़ के उस हिस्से को छोड़ देते हैं जो दाहिने आधे तल में स्थित है।

ग) हम ग्राफ़ के परिणामी भाग को 0y अक्ष पर सममित रूप से प्रदर्शित करते हैं।

घ) परिणामी ग्राफ चित्र में बिंदीदार रेखा में दिखाया गया है (चित्र 7).

2) 0x अक्ष के ऊपर कोई बिंदु नहीं है; हम 0x अक्ष पर बिंदुओं को अपरिवर्तित छोड़ते हैं।

3) 0x अक्ष के नीचे स्थित ग्राफ़ का भाग 0x के सापेक्ष सममित रूप से प्रदर्शित होता है।

4) परिणामी ग्राफ़ को एक बिंदीदार रेखा के साथ चित्र में दिखाया गया है (चित्र 8).

उदाहरण 5. फ़ंक्शन का ग्राफ़ बनाएं y = |(2|x| – 4) / (|x| + 3)|

1) सबसे पहले आपको फ़ंक्शन y = (2|x| – 4) / (|x| + 3) प्लॉट करना होगा। ऐसा करने के लिए, हम एल्गोरिथम 2 पर लौटते हैं।

a) फ़ंक्शन y = (2x – 4) / (x + 3) को सावधानीपूर्वक प्लॉट करें (चित्र 9).

नोटिस जो यह फ़ंक्शनभिन्नात्मक रैखिक है और इसका ग्राफ एक अतिपरवलय है। किसी वक्र को आलेखित करने के लिए, आपको सबसे पहले ग्राफ़ की अनंतस्पर्शी रेखाएँ ढूँढ़नी होंगी। क्षैतिज - y = 2/1 (अंश के अंश और हर में x के गुणांक का अनुपात), ऊर्ध्वाधर - x = -3.

2) हम ग्राफ़ के उस हिस्से को अपरिवर्तित छोड़ देंगे जो 0x अक्ष के ऊपर या उस पर है।

3) 0x अक्ष के नीचे स्थित ग्राफ़ का भाग 0x के सापेक्ष सममित रूप से प्रदर्शित किया जाएगा।

4) अंतिम ग्राफ चित्र में दिखाया गया है (चित्र 11).

वेबसाइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, स्रोत के लिंक की आवश्यकता होती है।

"प्राकृतिक लघुगणक" - 0.1. प्राकृतिक लघुगणक. 4. लघुगणकीय डार्ट्स। 0.04. 7.121.

"पावर फंक्शन ग्रेड 9" - यू. क्यूबिक परवलय। वाई = x3. 9वीं कक्षा की शिक्षिका लाडोशकिना आई.ए. वाई = x2. अतिपरवलय. 0. Y = xn, y = x-n जहां n दिया गया है प्राकृतिक संख्या. X. घातांक एक सम प्राकृत संख्या (2n) है।

"द्विघात फलन" - 1 परिभाषा द्विघात फंक्शन 2 किसी फ़ंक्शन के गुण 3 किसी फ़ंक्शन के ग्राफ़ 4 द्विघात असमानताएँ 5 निष्कर्ष। गुण: असमानताएँ: 8ए कक्षा के छात्र एंड्री गेर्लिट्ज़ द्वारा तैयार किया गया। योजना: ग्राफ़: -ए के लिए एकरसता का अंतराल > 0 के लिए< 0. Квадратичная функция. Квадратичные функции используются уже много лет.

"द्विघात फलन और उसका ग्राफ" - समाधान.y=4x A(0.5:1) 1=1 A-संबंधित है। जब a=1, सूत्र y=ax का रूप लेता है।

"8वीं कक्षा का द्विघात फलन" - 1) एक परवलय के शीर्ष की रचना करें। एक द्विघात फलन का ग्राफ आलेखित करना। एक्स। -7. फ़ंक्शन का ग्राफ बनाएं. बीजगणित 8वीं कक्षा के शिक्षक 496 बोविना स्कूल टी.वी.-1. निर्माण योजना। 2) सममिति अक्ष x=-1 की रचना करें। वाई

1. भिन्नात्मक रैखिक फलन और उसका ग्राफ

y = P(x) / Q(x) के रूप का एक फलन, जहां P(x) और Q(x) बहुपद हैं, भिन्नात्मक परिमेय फलन कहलाता है।

आप संभवतः परिमेय संख्याओं की अवधारणा से पहले से ही परिचित हैं। वैसे ही तर्कसंगत कार्यऐसे फलन हैं जिन्हें दो बहुपदों के भागफल के रूप में दर्शाया जा सकता है।

यदि एक भिन्नात्मक परिमेय फलन दो रैखिक फलनों का भागफल है - पहली डिग्री के बहुपद, अर्थात्। प्रपत्र का कार्य

y = (ax + b) / (cx + d), तो इसे भिन्नात्मक रैखिक कहा जाता है।

ध्यान दें कि फ़ंक्शन में y = (ax + b) / (cx + d), c ≠ 0 (अन्यथा फ़ंक्शन रैखिक y = ax/d + b/d हो जाता है) और a/c ≠ b/d (अन्यथा फ़ंक्शन स्थिर है)। रैखिक भिन्नात्मक फलन x = -d/c को छोड़कर सभी वास्तविक संख्याओं के लिए परिभाषित किया गया है। भिन्नात्मक रैखिक फलनों के ग्राफ़ उस ग्राफ़ y = 1/x से आकार में भिन्न नहीं होते हैं जिसे आप जानते हैं। एक वक्र जो फलन y = 1/x का ग्राफ है, कहलाता है अतिशयोक्ति. निरपेक्ष मान में x में असीमित वृद्धि के साथ, फ़ंक्शन y = 1/x निरपेक्ष मान में असीमित रूप से घटता है और ग्राफ़ की दोनों शाखाएं भुज तक पहुंचती हैं: दाईं ओर ऊपर से पहुंचती है, और बाईं ओर नीचे से। हाइपरबोला की शाखाएँ जिस रेखा तक पहुँचती हैं, उसे उसकी रेखाएँ कहा जाता है स्पर्शोन्मुख.

उदाहरण 1।

y = (2x + 1) / (x – 3).

समाधान।

आइए पूरे भाग का चयन करें: (2x + 1) / (x – 3) = 2 + 7/(x – 3)।

अब यह देखना आसान है कि इस फ़ंक्शन का ग्राफ़ निम्नलिखित परिवर्तनों द्वारा फ़ंक्शन y = 1/x के ग्राफ़ से प्राप्त किया गया है: 3 इकाई खंडों द्वारा दाईं ओर शिफ्ट, ओए अक्ष के साथ 7 बार खींचना और 2 द्वारा शिफ्ट करना इकाई खंड ऊपर की ओर।

किसी भी अंश y = (ax + b) / (cx + d) को "पूर्णांक भाग" को हाइलाइट करते हुए, इसी तरह से लिखा जा सकता है। नतीजतन, सभी भिन्नात्मक रैखिक कार्यों के ग्राफ़ अतिपरवलय हैं, जो समन्वय अक्षों के साथ विभिन्न तरीकों से स्थानांतरित होते हैं और ओए अक्ष के साथ खींचे जाते हैं।

किसी भी मनमाने ढंग से भिन्नात्मक-रैखिक फ़ंक्शन का ग्राफ़ बनाने के लिए, इस फ़ंक्शन को परिभाषित करने वाले भिन्न को बदलना बिल्कुल भी आवश्यक नहीं है। चूँकि हम जानते हैं कि ग्राफ़ एक अतिपरवलय है, इसलिए यह उन सीधी रेखाओं को खोजने के लिए पर्याप्त होगा जिन तक इसकी शाखाएँ पहुँचती हैं - अतिपरवलय x = -d/c और y = a/c के अनंतस्पर्शी।

उदाहरण 2.

फ़ंक्शन y = (3x + 5)/(2x + 2) के ग्राफ़ के स्पर्शोन्मुख खोजें।

समाधान।

x = -1 पर फ़ंक्शन परिभाषित नहीं है। इसका मतलब यह है कि सीधी रेखा x = -1 एक ऊर्ध्वाधर अनंतस्पर्शी के रूप में कार्य करती है। क्षैतिज अनंतस्पर्शी को खोजने के लिए, आइए जानें कि जब तर्क x निरपेक्ष मान में बढ़ता है तो फ़ंक्शन y(x) का मान क्या होता है।

ऐसा करने के लिए, भिन्न के अंश और हर को x से विभाजित करें:

y = (3 + 5/x) / (2 + 2/x).

x → ∞ के रूप में भिन्न की प्रवृत्ति 3/2 हो जाएगी। इसका मतलब यह है कि क्षैतिज अनंतस्पर्शी सीधी रेखा y = 3/2 है।

उदाहरण 3.

फ़ंक्शन y = (2x + 1)/(x + 1) को ग्राफ़ करें।

समाधान।

आइए भिन्न का "संपूर्ण भाग" चुनें:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

2 – 1/(x + 1).

अब यह देखना आसान है कि इस फ़ंक्शन का ग्राफ़ निम्नलिखित परिवर्तनों द्वारा फ़ंक्शन y = 1/x के ग्राफ़ से प्राप्त किया गया है: बाईं ओर 1 इकाई द्वारा बदलाव, ऑक्स के संबंध में एक सममित प्रदर्शन और द्वारा एक बदलाव ओए अक्ष के साथ ऊपर 2 इकाई खंड।

डोमेन D(y) = (-∞; -1)ᴗ(-1; +∞).

मानों की सीमा E(y) = (-∞; 2)ᴗ(2; +∞).

अक्षों के साथ प्रतिच्छेदन बिंदु: c Oy: (0; 1); सी बैल: (-1/2; 0). परिभाषा के क्षेत्र के प्रत्येक अंतराल पर फ़ंक्शन बढ़ता है।

उत्तर: चित्र 1.

2. भिन्नात्मक तर्कसंगत कार्य

y = P(x) / Q(x) के रूप के भिन्नात्मक परिमेय फलन पर विचार करें, जहां P(x) और Q(x) पहले से अधिक घात वाले बहुपद हैं।

ऐसे तर्कसंगत कार्यों के उदाहरण:

y = (x 3 – 5x + 6) / (x 7 – 6) या y = (x – 2) 2 (x + 1) / (x 2 + 3)।

यदि फ़ंक्शन y = P(x) / Q(x) पहले से अधिक डिग्री वाले दो बहुपदों के भागफल का प्रतिनिधित्व करता है, तो इसका ग्राफ, एक नियम के रूप में, अधिक जटिल होगा, और कभी-कभी इसे सटीक रूप से बनाना मुश्किल हो सकता है। , सभी विवरणों के साथ। हालाँकि, अक्सर उन तकनीकों के समान उपयोग करना पर्याप्त होता है जिन्हें हम पहले ही ऊपर प्रस्तुत कर चुके हैं।

माना कि भिन्न एक उचित भिन्न है (n< m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:

P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+

एल 1 /(एक्स – के एस) एमएस + एल 2 /(एक्स – के एस) एमएस-1 + … + एल एमएस /(एक्स – के एस) + …+

+ (बी 1 एक्स + सी 1) / (एक्स 2 +पी 1 एक्स + क्यू 1) एम1 + … + (बी एम1 एक्स + सी एम1) / (एक्स 2 +पी 1 एक्स + क्यू 1) + …+

+ (एम 1 एक्स + एन 1) / (एक्स 2 +पी टी एक्स + क्यू टी) एम1 + … + (एम एम1 एक्स + एन एम1) / (एक्स 2 +पी टी एक्स + क्यू टी)।

जाहिर है, भिन्नात्मक परिमेय फलन का ग्राफ प्राथमिक भिन्नों के ग्राफ के योग के रूप में प्राप्त किया जा सकता है।

भिन्नात्मक परिमेय फलनों का रेखांकन आलेखित करना

आइए भिन्नात्मक परिमेय फलन के ग्राफ़ बनाने के कई तरीकों पर विचार करें।

उदाहरण 4.

फ़ंक्शन y = 1/x 2 का ग्राफ़ बनाएं।

समाधान।

हम y = 1/x 2 का ग्राफ बनाने के लिए फ़ंक्शन y = x 2 के ग्राफ का उपयोग करते हैं और ग्राफ़ को "विभाजित" करने की तकनीक का उपयोग करते हैं।

डोमेन D(y) = (-∞; 0)ᴗ(0; +∞).

मानों की सीमा E(y) = (0; +∞).

अक्षों के साथ प्रतिच्छेदन का कोई बिंदु नहीं है। फ़ंक्शन सम है. अंतराल (-∞; 0) से सभी x के लिए बढ़ता है, x के लिए 0 से +∞ तक घटता है।

उत्तर: चित्र 2.

उदाहरण 5.

फ़ंक्शन y = (x 2 – 4x + 3) / (9 – 3x) का ग्राफ़ बनाएं।

समाधान।

डोमेन D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/ 3 + 1/3.

यहां हमने एक रैखिक फलन में गुणनखंडन, न्यूनीकरण और न्यूनीकरण की तकनीक का उपयोग किया।

उत्तर: चित्र 3.

उदाहरण 6.

फ़ंक्शन y = (x 2 – 1)/(x 2 + 1) का ग्राफ़ बनाएं।

समाधान।

परिभाषा का क्षेत्र D(y) = R है। चूँकि फलन सम है, ग्राफ़ कोटि के बारे में सममित है। ग्राफ़ बनाने से पहले, आइए अभिव्यक्ति को फिर से रूपांतरित करें, पूरे भाग पर प्रकाश डालें:

y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1).

ध्यान दें कि भिन्नात्मक परिमेय फलन के सूत्र में पूर्णांक भाग को अलग करना ग्राफ़ बनाते समय मुख्य कार्यों में से एक है।

यदि x → ±∞, तो y → 1, अर्थात। सीधी रेखा y = 1 एक क्षैतिज अनंतस्पर्शी है।

उत्तर: चित्र 4.

उदाहरण 7.

आइए फ़ंक्शन y = x/(x 2 + 1) पर विचार करें और इसका सबसे बड़ा मान सटीक रूप से खोजने का प्रयास करें, अर्थात। ग्राफ़ के दाहिने आधे भाग पर उच्चतम बिंदु। इस ग्राफ़ को सटीक रूप से बनाने के लिए आज का ज्ञान पर्याप्त नहीं है। जाहिर है, हमारा वक्र बहुत ऊंचा "उठ" नहीं सकता, क्योंकि हर तेजी से अंश से आगे निकलना शुरू कर देता है। आइए देखें कि क्या फ़ंक्शन का मान 1 के बराबर हो सकता है। ऐसा करने के लिए, हमें समीकरण x 2 + 1 = x, x 2 – x + 1 = 0 को हल करना होगा। इस समीकरण की कोई वास्तविक जड़ें नहीं हैं। इसका मतलब है कि हमारी धारणा ग़लत है. फ़ंक्शन का सबसे बड़ा मान ज्ञात करने के लिए, आपको यह पता लगाना होगा कि किस सबसे बड़े A पर समीकरण A = x/(x 2 + 1) का हल होगा। आइए मूल समीकरण को एक द्विघात समीकरण से बदलें: Ax 2 – x + A = 0. इस समीकरण का एक हल तब होता है जब 1 – 4A 2 ≥ 0 होता है। यहां से हमें सबसे बड़ा मान A = 1/2 मिलता है।

उत्तर: चित्र 5, अधिकतम y(x) = ½।

क्या आपके पास अभी भी प्रश्न हैं? क्या आप नहीं जानते कि फ़ंक्शंस का ग्राफ़ कैसे बनाया जाता है?
ट्यूटर से सहायता प्राप्त करने के लिए, पंजीकरण करें।
पहला पाठ निःशुल्क है!

वेबसाइट, सामग्री को पूर्ण या आंशिक रूप से कॉपी करते समय, स्रोत के लिंक की आवश्यकता होती है।