Sacando el grado del logaritmo. Protección de información personal
Mantener su privacidad es importante para nosotros. Por este motivo, hemos desarrollado una Política de Privacidad que describe cómo usamos y almacenamos su información. Revise nuestras prácticas de privacidad y háganos saber si tiene alguna pregunta.
Recopilación y uso de información personal.
La información personal se refiere a datos que pueden usarse para identificar o contactar a una persona específica.
Es posible que se le solicite que proporcione su información personal en cualquier momento cuando se comunique con nosotros.
A continuación se muestran algunos ejemplos de los tipos de información personal que podemos recopilar y cómo podemos usar dicha información.
Qué información personal recopilamos:
- Cuando envía una solicitud en el sitio, podemos recopilar diversa información, incluido su nombre, número de teléfono, dirección de correo electrónico, etc.
Cómo usamos tu información personal:
- La información personal que recopilamos nos permite comunicarnos con usted con ofertas únicas, promociones y otros eventos y próximos eventos.
- De vez en cuando, podemos utilizar su información personal para enviar avisos y comunicaciones importantes.
- También podemos utilizar información personal para fines internos, como realizar auditorías, análisis de datos e investigaciones diversas para mejorar los servicios que brindamos y brindarle recomendaciones sobre nuestros servicios.
- Si participa en un sorteo de premios, concurso o promoción similar, podremos utilizar la información que proporcione para administrar dichos programas.
Divulgación de información a terceros
No revelamos la información que recibimos de usted a terceros.
Excepciones:
- Si es necesario, de conformidad con la ley, un procedimiento judicial, en procedimientos legales y/o en base a solicitudes públicas o solicitudes de organismos gubernamentales de la Federación de Rusia, revelar su información personal. También podemos divulgar información sobre usted si determinamos que dicha divulgación es necesaria o apropiada para fines de seguridad, aplicación de la ley u otros fines de importancia pública.
- En caso de una reorganización, fusión o venta, podemos transferir la información personal que recopilamos al tercero sucesor correspondiente.
Protección de información personal
Tomamos precauciones, incluidas las administrativas, técnicas y físicas, para proteger su información personal contra pérdida, robo y uso indebido, así como contra acceso no autorizado, divulgación, alteración y destrucción.
Respetando su privacidad a nivel de empresa
Para garantizar que su información personal esté segura, comunicamos estándares de privacidad y seguridad a nuestros empleados y aplicamos estrictamente las prácticas de privacidad.
(del griego λόγος - "palabra", "relación" y ἀριθμός - "número") números b Residencia en a(log α b) se llama tal número C, Y b= una c, es decir, registros log α b=C Y b=aC son equivalentes. El logaritmo tiene sentido si a > 0, a ≠ 1, b > 0.
En otras palabras logaritmo números b Residencia en A formulado como un exponente al que se debe elevar un número a para obtener el numero b(El logaritmo existe sólo para números positivos).
De esta formulación se deduce que el cálculo x= log α b, equivale a resolver la ecuación a x =b.
Por ejemplo:
Iniciar sesión 2 8 = 3 porque 8 = 2 3 .
Destaquemos que la formulación indicada del logaritmo permite determinar inmediatamente valor logaritmo, cuando el número bajo el signo del logaritmo actúa como una potencia de la base. De hecho, la formulación del logaritmo permite justificar que si b=a c, entonces el logaritmo del número b Residencia en a es igual Con. También está claro que el tema de los logaritmos está estrechamente relacionado con el tema. potencias de un numero.
Calcular el logaritmo se llama logaritmo. Logaritmo es la operación matemática de tomar un logaritmo. Al tomar logaritmos, los productos de factores se transforman en sumas de términos.
Potenciación es la operación matemática inversa del logaritmo. Durante la potenciación, una base determinada se eleva hasta el grado de expresión sobre el cual se realiza la potenciación. En este caso, las sumas de términos se transforman en un producto de factores.
Muy a menudo, se utilizan logaritmos reales con bases 2 (binario), el número de Euler e ≈ 2,718 (logaritmo natural) y 10 (decimal).
En esta etapa es aconsejable considerar muestras de logaritmos iniciar sesión 7 2 , en √ 5, lg0.0001.
Y las entradas lg(-3), log -3 3.2, log -1 -4.3 no tienen sentido, ya que en la primera de ellas se coloca un número negativo bajo el signo del logaritmo, en la segunda hay un número negativo en la base, y en el tercero hay un número negativo bajo el signo del logaritmo y la unidad en la base.
Condiciones para determinar el logaritmo.
Vale la pena considerar por separado las condiciones a > 0, a ≠ 1, b > 0, bajo las cuales obtenemos definición de logaritmo. Consideremos por qué se tomaron estas restricciones. Una igualdad de la forma x = log α nos ayudará con esto b, llamada identidad logarítmica básica, que se deriva directamente de la definición de logaritmo dada anteriormente.
Tomemos la condición a≠1. Dado que uno elevado a cualquier potencia es igual a uno, entonces la igualdad x=log α b sólo puede existir cuando b=1, pero log 1 1 será cualquier número real. Para eliminar esta ambigüedad, tomamos a≠1.
Demostremos la necesidad de la condición. a>0. En a=0 según la formulación del logaritmo sólo puede existir cuando b=0. Y en consecuencia entonces iniciar sesión 0 0 puede ser cualquier número real distinto de cero, ya que cero elevado a cualquier potencia distinta de cero es cero. Esta ambigüedad puede eliminarse mediante la condición a≠0. Y cuando a<0 Tendríamos que rechazar el análisis de los valores racionales e irracionales del logaritmo, ya que un grado con exponente racional e irracional se define sólo para bases no negativas. Es por esta razón que se estipula la condición a>0.
Y la última condición b>0 se sigue de la desigualdad a>0, ya que x=log α b, y el valor del grado con base positiva a siempre positivo.
Características de los logaritmos.
Logaritmos caracterizado por distintivo características, lo que llevó a su uso generalizado para facilitar significativamente los cálculos minuciosos. Al pasar “al mundo de los logaritmos”, la multiplicación se transforma en una suma mucho más sencilla, la división se transforma en resta y la exponenciación y la extracción de raíces se transforman, respectivamente, en multiplicación y división por el exponente.
La formulación de logaritmos y una tabla de sus valores (para funciones trigonométricas) fue publicada por primera vez en 1614 por el matemático escocés John Napier. Las tablas logarítmicas, ampliadas y detalladas por otros científicos, se utilizaron ampliamente en cálculos científicos y de ingeniería y siguieron siendo relevantes hasta el uso de calculadoras electrónicas y computadoras.
Definición de logaritmo
El logaritmo de b en base a es el exponente al que se debe elevar a para obtener b.
Número e en matemáticas se acostumbra denotar el límite al que se esfuerza una expresión
Número e es numero irracional- un número inconmensurable con uno, no se puede expresar con precisión ni como un número entero ni como una fracción racional número.
Carta mi- primera letra de una palabra latina exponer- para lucirse, de ahí el nombre en matemáticas exponencial- funcion exponencial.
Número mi muy utilizado en matemáticas, y en todas las ciencias que de una forma u otra utilizan los cálculos matemáticos para sus necesidades.
Logaritmos. Propiedades de los logaritmos
Definición: El logaritmo de un número positivo b en su base es el exponente c al que se debe elevar el número a para obtener el número b.

Identidad logarítmica básica:


7) Fórmula para trasladarse a una nueva base:
lna = log e a, e ≈ 2,718…
Problemas y pruebas sobre el tema “Logaritmos. Propiedades de los logaritmos"
- Logaritmos: temas importantes para repasar el Examen Estatal Unificado de Matemáticas
Para completar con éxito las tareas sobre este tema, debe conocer la definición de logaritmo, las propiedades de los logaritmos, la identidad logarítmica básica, las definiciones de logaritmos decimales y naturales. Los principales tipos de problemas sobre este tema son los problemas que implican el cálculo y la transformación de expresiones logarítmicas. Consideremos su solución usando los siguientes ejemplos.
Solución: Usando las propiedades de los logaritmos, obtenemos
Solución: Usando las propiedades de los grados, obtenemos
1) (2 2) registro 2 5 =(2 registro 2 5) 2 =5 2 =25
Propiedades de logaritmos, formulaciones y pruebas.
Los logaritmos tienen una serie de propiedades características. En este artículo veremos los principales. propiedades de los logaritmos. Aquí daremos sus formulaciones, escribiremos las propiedades de los logaritmos en forma de fórmulas, mostraremos ejemplos de su aplicación y también proporcionaremos pruebas de las propiedades de los logaritmos.
Navegación de páginas.
Propiedades básicas de logaritmos, fórmulas.
Para facilitar la memoria y el uso, imaginemos propiedades básicas de los logaritmos en forma de lista de fórmulas. En el siguiente párrafo daremos sus formulaciones, evidencias, ejemplos de uso y explicaciones necesarias.
y la propiedad del logaritmo del producto de n números positivos: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .
 , donde a>0, a≠1, x>0, y>0.
, donde a>0, a≠1, x>0, y>0. , a>0 , a≠1 , b>0 , b≠1 .
, a>0 , a≠1 , b>0 , b≠1 . , a>0 , a≠1 , b>0 , p y q son números reales, q≠0 , en particular para b=a tenemos
, a>0 , a≠1 , b>0 , p y q son números reales, q≠0 , en particular para b=a tenemos  .
.Formulaciones y pruebas de propiedades.
Procedemos a la formulación y demostración de las propiedades escritas de los logaritmos. Todas las propiedades de los logaritmos se prueban con base en la definición del logaritmo y la identidad logarítmica básica que se deriva de él, así como las propiedades del grado.
Empecemos con propiedades del logaritmo de uno. Su formulación es la siguiente: el logaritmo de la unidad es igual a cero, es decir, registrar un 1=0 para cualquier a>0, a≠1. La demostración no es difícil: dado que a 0 =1 para cualquier a que cumpla las condiciones anteriores a>0 y a≠1, entonces la igualdad log a 1=0 a demostrar se deriva inmediatamente de la definición del logaritmo.
Pongamos ejemplos de la aplicación de la propiedad considerada: log 3 1=0, log1=0 y .
Pasemos a la siguiente propiedad: el logaritmo de un número igual a la base es igual a uno, eso es, iniciar sesión a = 1 para a>0, a≠1. De hecho, dado que a 1 =a para cualquier a, entonces, por definición del logaritmo, log a a=1.
Ejemplos del uso de esta propiedad de los logaritmos son las igualdades log 5 5=1, log 5,6 5,6 y lne=1.
El logaritmo de una potencia de un número igual a la base del logaritmo es igual al exponente.. Esta propiedad del logaritmo corresponde a una fórmula de la forma iniciar sesión a ap =p, donde a>0, a≠1 yp – cualquier número real. Esta propiedad se deriva directamente de la definición del logaritmo. Tenga en cuenta que le permite indicar inmediatamente el valor del logaritmo, si es posible representar el número bajo el signo del logaritmo como una potencia de la base, hablaremos más sobre esto en el artículo sobre cálculo de logaritmos;
Por ejemplo, log 2 2 7 =7, log10 -4 =-4 y ![]() .
.
Logaritmo del producto de dos números positivos. xey es igual al producto de los logaritmos de estos números: log a (x y)=log a x+log a y, a>0 , a≠1 . Demostremos la propiedad del logaritmo de un producto. Debido a las propiedades del grado a log a x+log a y =a log a x ·a log a y, y dado que por la identidad logarítmica principal a log a x =x y a log a y =y, entonces a log a x ·a log a y =x·y. Por lo tanto, un log a x+log a y =x·y, de donde, según la definición de logaritmo, se sigue la igualdad que se está demostrando.
Mostremos ejemplos del uso de la propiedad del logaritmo de un producto: log 5 (2 3)=log 5 2+log 5 3 y ![]() .
.
La propiedad del logaritmo de un producto se puede generalizar al producto de un número finito n de números positivos x 1 , x 2 ,…, x n como log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Esta igualdad se puede demostrar sin problemas mediante el método de inducción matemática.
Por ejemplo, el logaritmo natural del producto se puede sustituir por la suma de tres logaritmos naturales de los números 4, e, y.
Logaritmo del cociente de dos números positivos xey es igual a la diferencia entre los logaritmos de estos números. La propiedad del logaritmo de un cociente corresponde a una fórmula de la forma  , donde a>0, a≠1, xey son algunos números positivos. La validez de esta fórmula está probada al igual que la fórmula del logaritmo de un producto: ya que
, donde a>0, a≠1, xey son algunos números positivos. La validez de esta fórmula está probada al igual que la fórmula del logaritmo de un producto: ya que  , entonces por definición del logaritmo
, entonces por definición del logaritmo  .
.
A continuación se muestra un ejemplo del uso de esta propiedad del logaritmo: ![]() .
.
Movámonos a propiedad del logaritmo de la potencia. El logaritmo de un grado es igual al producto del exponente por el logaritmo del módulo de la base de ese grado. Escribamos esta propiedad del logaritmo de una potencia como fórmula: log a b p =p·log a |b|, donde a>0, a≠1, b y p son números tales que el grado b p tiene sentido y b p >0.
Primero demostramos que esta propiedad es positiva b. La identidad logarítmica básica nos permite representar el número b como un log a b , luego b p =(a log a b) p , y la expresión resultante, debido a la propiedad de la potencia, es igual a a p·log a b . Entonces llegamos a la igualdad b p =a p·log a b, de la cual, por la definición de logaritmo, concluimos que log a b p =p·log a b.
Queda por demostrar esta propiedad para b negativo. Aquí notamos que la expresión log a b p para b negativo tiene sentido solo para exponentes pares p (ya que el valor del grado b p debe ser mayor que cero, de lo contrario el logaritmo no tendrá sentido), y en este caso b p =|b| pag. Entonces b p =|b| p =(a log a |b|) p =a p·log a |b| , de donde log a b p =p·log a |b| .
Por ejemplo,  y ln(-3) 4 =4·ln|-3|=4·ln3 .
y ln(-3) 4 =4·ln|-3|=4·ln3 .
Se deduce de la propiedad anterior propiedad del logaritmo de la raíz: el logaritmo de la raíz n-ésima es igual al producto de la fracción 1/n por el logaritmo de la expresión radical, es decir, donde a>0, a≠1, n es un número natural mayor que uno, b>0 .
La prueba se basa en la igualdad (ver definición de exponente con exponente fraccionario), que es válida para cualquier b positivo, y la propiedad del logaritmo del exponente:  .
.
A continuación se muestra un ejemplo del uso de esta propiedad: ![]() .
.
Ahora demostremos fórmula para pasar a una nueva base logarítmica tipo  . Para ello basta con demostrar la validez de la igualdad log c b=log a b·log c a. La identidad logarítmica básica nos permite representar el número b como log a b, luego log c b=log c a log a b. Queda por utilizar la propiedad del logaritmo del grado: log c a log a b =log a b·log c a . Esto demuestra la igualdad log c b=log a b·log c a, lo que significa que también se demuestra la fórmula para la transición a una nueva base del logaritmo.
. Para ello basta con demostrar la validez de la igualdad log c b=log a b·log c a. La identidad logarítmica básica nos permite representar el número b como log a b, luego log c b=log c a log a b. Queda por utilizar la propiedad del logaritmo del grado: log c a log a b =log a b·log c a . Esto demuestra la igualdad log c b=log a b·log c a, lo que significa que también se demuestra la fórmula para la transición a una nueva base del logaritmo.  .
.
Mostremos un par de ejemplos del uso de esta propiedad de los logaritmos: y  .
.
La fórmula para pasar a una nueva base le permite pasar a trabajar con logaritmos que tienen una base "conveniente". Por ejemplo, se puede utilizar para cambiar a logaritmos naturales o decimales para poder calcular el valor de un logaritmo a partir de una tabla de logaritmos. La fórmula para pasar a una nueva base de logaritmo también permite, en algunos casos, encontrar el valor de un logaritmo determinado cuando se conocen los valores de algunos logaritmos con otras bases.
A menudo se utiliza un caso especial de la fórmula para la transición a una nueva base logarítmica para c=b de la forma. Esto muestra que log a b y log b a son números mutuamente inversos. P.ej,  .
.
También se utiliza a menudo la fórmula, que es conveniente para encontrar los valores de logaritmos. Para confirmar nuestras palabras, mostraremos cómo se puede utilizar para calcular el valor de un logaritmo de la forma. Tenemos  . Para probar la fórmula, basta con utilizar la fórmula para pasar a una nueva base del logaritmo a:
. Para probar la fórmula, basta con utilizar la fórmula para pasar a una nueva base del logaritmo a:  .
.
Queda por demostrar las propiedades de comparación de logaritmos.
Usemos el método opuesto. Supongamos que para a 1 >1, a 2 >1 y a 1 2 y para 0 1, log a 1 b≤log a 2 b es verdadero. Con base en las propiedades de los logaritmos, estas desigualdades se pueden reescribir como  Y
Y  respectivamente, y de ellos se deduce que log b a 1 ≤log b a 2 y log b a 1 ≥log b a 2, respectivamente. Entonces, de acuerdo con las propiedades de potencias con las mismas bases, las igualdades b log b a 1 ≥b log b a 2 y b log b a 1 ≥b log b a 2 deben cumplirse, es decir, a 1 ≥a 2 . Entonces llegamos a una contradicción con la condición a 1 2. Esto completa la prueba.
respectivamente, y de ellos se deduce que log b a 1 ≤log b a 2 y log b a 1 ≥log b a 2, respectivamente. Entonces, de acuerdo con las propiedades de potencias con las mismas bases, las igualdades b log b a 1 ≥b log b a 2 y b log b a 1 ≥b log b a 2 deben cumplirse, es decir, a 1 ≥a 2 . Entonces llegamos a una contradicción con la condición a 1 2. Esto completa la prueba.
Propiedades básicas de los logaritmos.
- Materiales para la lección.
- Descargar todas las fórmulas
- log a x n = n · log a x ;


Los logaritmos, como cualquier número, se pueden sumar, restar y transformar de todas las formas posibles. Pero como los logaritmos no son exactamente números ordinarios, aquí existen reglas, que se llaman propiedades principales.
Definitivamente necesitas conocer estas reglas; sin ellas no se puede resolver ni un solo problema logarítmico serio. Además, hay muy pocos: puedes aprender todo en un día. Entonces empecemos.
Sumar y restar logaritmos
Considere dos logaritmos con las mismas bases: log a x y log a y. Luego se pueden sumar y restar, y:
Entonces, la suma de logaritmos es igual al logaritmo del producto y la diferencia es igual al logaritmo del cociente. Tenga en cuenta: el punto clave aquí es motivos idénticos. Si los motivos son diferentes, ¡estas reglas no funcionan!
Estas fórmulas te ayudarán a calcular una expresión logarítmica incluso cuando no se consideran sus partes individuales (consulta la lección “¿Qué es un logaritmo”). Eche un vistazo a los ejemplos y vea:
Tarea. Encuentra el valor de la expresión: log 6 4 + log 6 9.
Como los logaritmos tienen las mismas bases, usamos la fórmula de suma:
registro 6 4 + registro 6 9 = registro 6 (4 9) = registro 6 36 = 2.
Tarea. Encuentra el valor de la expresión: log 2 48 − log 2 3.
Las bases son las mismas, usamos la fórmula de diferencia:
registro 2 48 − registro 2 3 = registro 2 (48: 3) = registro 2 16 = 4.
Tarea. Encuentra el valor de la expresión: log 3 135 − log 3 5.
Nuevamente las bases son las mismas, entonces tenemos:
registro 3 135 − registro 3 5 = registro 3 (135: 5) = registro 3 27 = 3.
Como puedes ver, las expresiones originales se componen de logaritmos "malos", que no se calculan por separado. Pero después de las transformaciones se obtienen números completamente normales. Muchas pruebas se basan en este hecho. Sí, en el Examen Estatal Unificado se ofrecen expresiones tipo test con toda seriedad (a veces prácticamente sin cambios).
Extrayendo el exponente del logaritmo
Ahora compliquemos un poco la tarea. ¿Qué pasa si la base o argumento de un logaritmo es una potencia? Entonces el exponente de este grado se puede sacar del signo del logaritmo según las siguientes reglas:
Es fácil ver que la última regla sigue a las dos primeras. Pero es mejor recordarlo de todos modos; en algunos casos, esto reducirá significativamente la cantidad de cálculos.
Por supuesto, todas estas reglas tienen sentido si se observa la ODZ del logaritmo: a > 0, a ≠ 1, x > 0. Y una cosa más: aprende a aplicar todas las fórmulas no solo de izquierda a derecha, sino también al revés. , es decir. Puede ingresar los números antes del signo del logaritmo en el propio logaritmo. Esto es lo que más a menudo se requiere.
Tarea. Encuentra el valor de la expresión: log 7 49 6 .
Eliminemos el grado en el argumento usando la primera fórmula:
registro 7 49 6 = 6 registro 7 49 = 6 2 = 12
Tarea. Encuentra el significado de la expresión:
[Título de la imagen]
Tenga en cuenta que el denominador contiene un logaritmo, cuya base y argumento son potencias exactas: 16 = 2 4; 49 = 7 2. Tenemos:
 [Título de la imagen]
[Título de la imagen]
Creo que el último ejemplo requiere alguna aclaración. ¿A dónde se han ido los logaritmos? Hasta el último momento trabajamos sólo con el denominador. Presentamos la base y el argumento del logaritmo allí en forma de potencias y eliminamos los exponentes: obtuvimos una fracción de "tres pisos".
Ahora veamos la fracción principal. El numerador y el denominador contienen el mismo número: log 2 7. Como log 2 7 ≠ 0, podemos reducir la fracción: 2/4 permanecerá en el denominador. Según las reglas de la aritmética, el cuatro se puede trasladar al numerador, que es lo que se hizo. El resultado fue la respuesta: 2.
Transición a una nueva fundación.
Hablando de las reglas para sumar y restar logaritmos, enfaticé específicamente que solo funcionan con las mismas bases. ¿Qué pasa si las razones son diferentes? ¿Qué pasa si no son potencias exactas del mismo número?
Las fórmulas para la transición a una nueva base vienen al rescate. Formulémoslos en forma de teorema:
Sea el logaritmo log ax. Entonces, para cualquier número c tal que c > 0 y c ≠ 1, la igualdad es verdadera:
![]() [Título de la imagen]
[Título de la imagen]
En particular, si hacemos c = x, obtenemos:
![]() [Título de la imagen]
[Título de la imagen]
De la segunda fórmula se deduce que la base y el argumento del logaritmo se pueden intercambiar, pero en este caso se “da la vuelta” a toda la expresión, es decir el logaritmo aparece en el denominador.
Estas fórmulas rara vez se encuentran en expresiones numéricas ordinarias. Es posible evaluar qué tan convenientes son solo al resolver ecuaciones y desigualdades logarítmicas.
Sin embargo, hay problemas que no pueden resolverse en absoluto excepto trasladándose a una nueva fundación. Veamos un par de estos:
Tarea. Encuentra el valor de la expresión: log 5 16 log 2 25.
Tenga en cuenta que los argumentos de ambos logaritmos contienen potencias exactas. Saquemos los indicadores: log 5 16 = log 5 2 4 = 4log 5 2; registro 2 25 = registro 2 5 2 = 2 registro 2 5;
Ahora “invirtamos” el segundo logaritmo:
[Título de la imagen]
Como el producto no cambia al reorganizar los factores, multiplicamos tranquilamente cuatro por dos y luego nos ocupamos de los logaritmos.
Tarea. Encuentra el valor de la expresión: log 9 100 lg 3.
La base y el argumento del primer logaritmo son potencias exactas. Anotemos esto y eliminemos los indicadores:
[Título de la imagen]
Ahora eliminemos el logaritmo decimal moviéndolo a una nueva base:
[Título de la imagen]
Identidad logarítmica básica
A menudo, en el proceso de solución es necesario representar un número como un logaritmo con una base determinada. En este caso nos ayudarán las siguientes fórmulas:
- n = log a a n
-
En el primer caso, el número n se convierte en el exponente del argumento. El número n puede ser absolutamente cualquier cosa, porque es sólo un valor de logaritmo.
La segunda fórmula es en realidad una definición parafraseada. Así se llama: la identidad logarítmica básica.
De hecho, ¿qué sucede si el número b se eleva a tal potencia que el número b elevado a esta potencia da el número a? Así es: el resultado es el mismo número a. Lea este párrafo con atención nuevamente; muchas personas se quedan estancadas en él.
Al igual que las fórmulas para pasar a una nueva base, la identidad logarítmica básica es a veces la única solución posible.
[Título de la imagen]
Tenga en cuenta que log 25 64 = log 5 8; simplemente tomamos el cuadrado de la base y el argumento del logaritmo. Teniendo en cuenta las reglas para multiplicar potencias con la misma base, obtenemos:
[Título de la imagen]
Si alguien no lo sabe, esta fue una tarea real del Examen Estatal Unificado :)
Unidad logarítmica y cero logarítmico
En conclusión, daré dos identidades que difícilmente pueden llamarse propiedades; más bien, son consecuencias de la definición del logaritmo. Aparecen constantemente en los problemas y, sorprendentemente, crean problemas incluso para los estudiantes "avanzados".
- log a a = 1 es una unidad logarítmica. Recuerda de una vez por todas: el logaritmo de cualquier base a de esa base es igual a uno.
- log a 1 = 0 es cero logarítmico. La base a puede ser cualquier cosa, pero si el argumento contiene uno, ¡el logaritmo es igual a cero! Porque a 0 = 1 es consecuencia directa de la definición.
Esas son todas las propiedades. ¡Asegúrate de practicar poniéndolos en práctica! Descargue la hoja de trucos al comienzo de la lección, imprímala y resuelva los problemas.
Logaritmo. Propiedades del logaritmo (suma y resta).
Propiedades del logaritmo seguir de su definición. Y entonces el logaritmo del número. b Residencia en A se define como el exponente al que se debe elevar un número a para obtener el numero b(El logaritmo existe sólo para números positivos).
De esta formulación se deduce que el cálculo x=log a b, equivale a resolver la ecuación ax=b. Por ejemplo, iniciar sesión 2 8 = 3 porque 8 = 2 3 . La formulación del logaritmo permite justificar que si b=a c, entonces el logaritmo del número b Residencia en a es igual Con. También está claro que el tema de los logaritmos está estrechamente relacionado con el tema de las potencias.
Con logaritmos, como con cualquier número, puedes hacer operaciones de suma, resta y transformarnos en todos los sentidos posibles. Pero debido al hecho de que los logaritmos no son números completamente ordinarios, aquí se aplican sus propias reglas especiales, que se llaman propiedades principales.
Sumar y restar logaritmos.
Tomemos dos logaritmos con las mismas bases: registrar una x Y iniciar sesión y. Entonces es posible realizar operaciones de suma y resta:
Como podemos ver, suma de logaritmos es igual al logaritmo del producto, y diferencia logaritmos- logaritmo del cociente. Además, esto es cierto si los números A, X Y en positivo y un ≠ 1.
Es importante señalar que el aspecto principal en estas fórmulas son las mismas bases. Si los motivos son diferentes, ¡estas reglas no se aplican!
Las reglas para sumar y restar logaritmos con las mismas bases se leen no solo de izquierda a derecha, sino también al revés. Como resultado, tenemos los teoremas para el logaritmo del producto y el logaritmo del cociente.
Logaritmo del producto dos números positivos son iguales a la suma de sus logaritmos ; reformulando este teorema obtenemos lo siguiente si los números A, X Y en positivo y un ≠ 1, Eso:
Logaritmo del cociente dos números positivos es igual a la diferencia entre los logaritmos del dividendo y el divisor. Para decirlo de otra manera, si los números A, X Y en positivo y un ≠ 1, Eso:
Apliquemos los teoremas anteriores para resolver ejemplos:
si los numeros X Y en son negativos, entonces fórmula del logaritmo del producto pierde sentido. Por tanto, está prohibido escribir:
ya que las expresiones log 2 (-8) y log 2 (-4) no están definidas en absoluto (función logarítmica en= registro 2 X definido sólo para valores de argumento positivos X).
Teorema del producto aplicable no sólo para dos, sino también para un número ilimitado de factores. Esto significa que por cada natural k y cualquier numero positivo X 1 , X 2 , . . . ,xn hay una identidad:
De teorema del cociente logaritmo Se puede obtener una propiedad más del logaritmo. Es de conocimiento común que el registro a 1= 0, por lo tanto
Esto significa que hay una igualdad:
Logaritmos de dos números recíprocos por la misma razón se diferenciarán entre sí únicamente por el signo. Entonces:
Logaritmo. Propiedades de los logaritmos
Logaritmo. Propiedades de los logaritmos
Consideremos la igualdad. Conozcamos los valores de y y queremos encontrar el valor de .
Es decir, buscamos el exponente por el cual debemos amartillarlo para obtener .
Dejar
 una variable puede tomar cualquier valor real, entonces se imponen las siguientes restricciones a las variables: o" title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″ />
una variable puede tomar cualquier valor real, entonces se imponen las siguientes restricciones a las variables: o" title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″ />Si conocemos los valores de y , y nos enfrentamos a la tarea de encontrar la incógnita, entonces para ello se introduce una operación matemática, que se llama logaritmo.
Para encontrar el valor tomamos logaritmo de un número Por base :
El logaritmo de un número respecto a su base es el exponente al que se debe elevar para obtener.
Eso es identidad logarítmica básica:
o» título=»a>o»/> , 1″ título=»a1″/>, 0″ título=»b>0″/>
es esencialmente una notación matemática definiciones de logaritmo.
La operación matemática del logaritmo es la inversa de la operación de exponenciación, por lo que propiedades de los logaritmos están estrechamente relacionados con las propiedades de grado.
Enumeremos los principales. propiedades de los logaritmos:
(o" título="a>o"/> , 1″ título=»a1″/>, 0″ título=»b>0″/>, 0,
d>0″/>, 1″ título=”d1″/>
4.

5.

El siguiente grupo de propiedades le permite representar el exponente de una expresión bajo el signo del logaritmo, o colocándose en la base del logaritmo en forma de coeficiente delante del signo del logaritmo:
6.

7.

8.

9.

El siguiente grupo de fórmulas le permite pasar de un logaritmo con una base dada a un logaritmo con una base arbitraria y se llama Fórmulas para mudarse a una nueva base.:
10.

12. (corolario de la propiedad 11)

Las siguientes tres propiedades no son muy conocidas, pero se utilizan a menudo al resolver ecuaciones logarítmicas o al simplificar expresiones que contienen logaritmos:
13.

14.

15.

Casos especiales:
 — logaritmo decimal
— logaritmo decimal — logaritmo natural
— logaritmo naturalAl simplificar expresiones que contienen logaritmos, se utiliza un enfoque general:
1. Representamos fracciones decimales como fracciones ordinarias.
2. Representamos los números mixtos como fracciones impropias.
3. Descomponemos los números en la base del logaritmo y bajo el signo del logaritmo en factores simples.
4. Intentamos reducir todos los logaritmos a la misma base.
5. Aplicar las propiedades de los logaritmos.
Veamos ejemplos de expresiones simplificadas que contienen logaritmos.
Ejemplo 1.
Calcular:
Simplifiquemos todos los exponentes: nuestra tarea es reducirlos a logaritmos, cuya base sea el mismo número que la base del exponente.
==(por propiedad 7)=(por propiedad 6) =
Sustituyamos los indicadores que obtuvimos en la expresión original. Obtenemos:
Respuesta: 5.25
Ejemplo 2. Calcular:

Reduzcamos todos los logaritmos a base 6 (en este caso, los logaritmos del denominador de la fracción “migrarán” al numerador):
Descompongamos los números bajo el signo de logaritmo en factores simples:
Apliquemos las propiedades 4 y 6:
Introduzcamos el reemplazo.
Obtenemos:

Respuesta 1
Logaritmo . Identidad logarítmica básica.
Propiedades de los logaritmos. Logaritmo decimal. Logaritmo natural.
Logaritmo número positivo N a la base (b > 0, b 1) es el exponente x al que se debe elevar b para obtener N .
Esta entrada equivale a lo siguiente: segundo x = norte .
Ejemplos: log 3 81 = 4, ya que 3 4 = 81;
iniciar sesión 1/3 27 = – 3, ya que (1/3) - 3 = 3 3 = 27.
La definición anterior de logaritmo se puede escribir como una identidad:

Propiedades básicas de los logaritmos.
2) iniciar sesión 1 = 0, ya que b 0 = 1 .
3) El logaritmo del producto es igual a la suma de los logaritmos de los factores:
4) El logaritmo del cociente es igual a la diferencia entre los logaritmos del dividendo y el divisor:
5) El logaritmo de una potencia es igual al producto del exponente por el logaritmo de su base:
La consecuencia de esta propiedad es la siguiente: logaritmo de la raíz igual al logaritmo del número radical dividido por la potencia de la raíz:

6) Si la base del logaritmo es un grado, entonces el valor el inverso del exponente se puede sacar como una rima logarítmica:

Las dos últimas propiedades se pueden combinar en una:

7) Fórmula del módulo de transición (es decir, transición de una base de logaritmo a otra base):

En el caso especial cuando N=a tenemos:
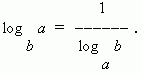
logaritmo decimal llamado logaritmo base 10. Se denomina LG, es decir. registro 10 norte= iniciar sesión norte. Logaritmos de los números 10, 100, 1000, . p son 1, 2, 3,…, respectivamente, es decir tener tantos positivos
unidades, cuántos ceros hay en un número logarítmico después del uno. Logaritmos de los números 0,1, 0,01, 0,001,. p son respectivamente –1, –2, –3,…, es decir tener tantos unos negativos como ceros hay en el número logarítmico antes del uno (incluidos los números enteros cero). Los logaritmos de otros números tienen una parte fraccionaria llamada mantisa. La parte entera de un logaritmo se llama característica. Para uso práctico, los logaritmos decimales son los más convenientes.
Logaritmo natural llamado logaritmo base mi. Se denota por ln, es decir registro mi norte= iniciar sesión norte. Número mi es irracional, su valor aproximado es 2.718281828. Es el límite al que tiende el número (1 + 1 / norte) norte con aumento ilimitado norte(cm. primer límite maravilloso en la página "Límites de secuencia numérica").
Por extraño que parezca, los logaritmos naturales resultaron muy convenientes a la hora de realizar diversos tipos de operaciones relacionadas con el análisis de funciones. Calcular logaritmos en base. mi mucho más rápido que por cualquier otro motivo.
- ¿Qué se necesita hoy para adoptar un niño en Rusia? La adopción en Rusia, además de una decisión personal responsable, implica una serie de procedimientos de verificación estatal de los candidatos. Una selección rigurosa en la etapa preparatoria contribuye a más […]
- Información gratuita sobre TIN u OGRN del registro fiscal en toda Rusia - en línea En el Portal de Servicios Fiscales Unificados, información sobre el registro estatal de personas jurídicas, empresarios individuales, […]
- Castigo por conducir sin documentos (licencia de conducir, seguro, STS) En ocasiones, por olvido, los conductores se ponen al volante sin licencia y reciben una multa por conducir sin documentos. Nos gustaría recordarles que un entusiasta de los automóviles debe tener […]
- Flores para hombres. ¿Qué flores puedes regalarle a un hombre? ¿Qué flores puedes regalarle a un hombre? No hay muchas flores “masculinas”, pero sí algunas que se regalan a los hombres. Una pequeña lista de flores frente a ti: crisantemos. Rosas. Claveles. […]
- Una nota interna es una forma especial de documento que se utiliza en el entorno interno de una empresa y sirve para resolver rápidamente los problemas de producción actuales. Normalmente, este documento se redacta con el fin de presentar algunos […]
- ¿Cuándo y cómo recibir la parte financiada de su pensión de Sberbank? Sberbank es un banco asociado del fondo de pensiones estatal. En base a esto, los ciudadanos que se registraron para una pensión de capitalización podrían transferir la parte financiada […]
- Prestaciones por hijos en Ulyanovsk y la región de Ulyanovsk en 2018 Además, en todas las regiones operan programas aprobados por la legislación federal. Veamos quién puede contar con qué beneficios. Cómo las autoridades regionales […]
- Orientación detallada sobre cómo redactar un poder para representar los intereses de una persona ante los tribunales. En un reclamo civil o de arbitraje, en un caso administrativo o penal, los intereses tanto del demandante como del demandado pueden ser representados por un abogado: […]
Logaritmo de un número norte Residencia en A llamado exponente X , al que necesitas construir A para obtener el numero norte
Siempre que  ,
, ,
,

De la definición de logaritmo se deduce que  , es decir.
, es decir.
 - esta igualdad es la identidad logarítmica básica.
- esta igualdad es la identidad logarítmica básica.
Los logaritmos en base 10 se llaman logaritmos decimales. En lugar de  escribir
escribir  .
.
Logaritmos a la base mi
se llaman naturales y se designan  .
.
Propiedades básicas de los logaritmos.
El logaritmo de la unidad es igual a cero para cualquier base.

El logaritmo del producto es igual a la suma de los logaritmos de los factores.
3) El logaritmo del cociente es igual a la diferencia de los logaritmos



Factor  llamado módulo de transición de logaritmos a la base a
a logaritmos en la base b
.
llamado módulo de transición de logaritmos a la base a
a logaritmos en la base b
.
Usando las propiedades 2 a 5, a menudo es posible reducir el logaritmo de una expresión compleja al resultado de operaciones aritméticas simples con logaritmos.
Por ejemplo, 
Estas transformaciones de un logaritmo se denominan logaritmos. Las transformaciones inversas a los logaritmos se llaman potenciación.
Capítulo 2. Elementos de la matemática superior.
1. Límites
Límite de la función  es un número finito A si, como xx
0
para cada predeterminado
es un número finito A si, como xx
0
para cada predeterminado  , existe tal número
, existe tal número  que tan pronto como
que tan pronto como  , Eso
, Eso  .
.

Una función que tiene límite difiere de él en una cantidad infinitesimal:  , dónde- b.m.v., es decir
, dónde- b.m.v., es decir  .
.
Ejemplo. Considere la función  .
.
Al esforzarse  , función y
tiende a cero:
, función y
tiende a cero: 
1.1. Teoremas básicos sobre límites.
El límite de un valor constante es igual a este valor constante.
 .
.
El límite de la suma (diferencia) de un número finito de funciones es igual a la suma (diferencia) de los límites de estas funciones.
El límite del producto de un número finito de funciones es igual al producto de los límites de estas funciones.
El límite del cociente de dos funciones es igual al cociente de los límites de estas funciones si el límite del denominador no es cero.

Límites maravillosos
 ,
,
 , Dónde
, Dónde 
1.2. Ejemplos de cálculo de límites

Sin embargo, no todos los límites se calculan tan fácilmente. Más a menudo, calcular el límite se reduce a revelar una incertidumbre del tipo:  o .
o .
 .
.
2. Derivada de una función
Tengamos una función  , continua en el segmento
, continua en el segmento  .
.
Argumento  consiguió algún aumento
consiguió algún aumento  . Entonces la función recibirá un incremento.
. Entonces la función recibirá un incremento.  .
.
Valor del argumento  corresponde al valor de la función
corresponde al valor de la función  .
.
Valor del argumento  corresponde al valor de la función.
corresponde al valor de la función.
Por eso, .

Encontremos el límite de esta relación en  . Si este límite existe, entonces se llama derivada de la función dada.
. Si este límite existe, entonces se llama derivada de la función dada.


Definición 3 Derivada de una función dada 
 por argumento
por argumento  Se llama límite de la relación entre el incremento de una función y el incremento del argumento, cuando el incremento del argumento tiende arbitrariamente a cero.
Se llama límite de la relación entre el incremento de una función y el incremento del argumento, cuando el incremento del argumento tiende arbitrariamente a cero.
Derivada de una función  puede designarse de la siguiente manera:
puede designarse de la siguiente manera:
 ;
;
 ;
;
 ;
;
 .
.
Definición 4La operación de encontrar la derivada de una función se llama diferenciación.
2.1. Significado mecánico de derivada.
Consideremos el movimiento rectilíneo de algún cuerpo rígido o punto material.
Deja que en algún momento 
 punto en movimiento
punto en movimiento  estaba a una distancia
estaba a una distancia  desde la posición inicial
desde la posición inicial  .
.

Después de algún período de tiempo  ella se movió una distancia
ella se movió una distancia  . Actitud
. Actitud  =
= - velocidad media de un punto material
- velocidad media de un punto material  . Encontremos el límite de esta relación, teniendo en cuenta que
. Encontremos el límite de esta relación, teniendo en cuenta que  .
.
En consecuencia, determinar la velocidad instantánea de movimiento de un punto material se reduce a encontrar la derivada de la trayectoria con respecto al tiempo.
2.2. Valor geométrico de la derivada.
Tengamos una función definida gráficamente.  .
.

Arroz. 1. Significado geométrico de la derivada.
Si  , luego señala
, luego señala  , se moverá a lo largo de la curva, acercándose al punto
, se moverá a lo largo de la curva, acercándose al punto  .
.

Por eso  , es decir. el valor de la derivada para un valor dado del argumento
, es decir. el valor de la derivada para un valor dado del argumento  numéricamente igual a la tangente del ángulo formado por la tangente en un punto dado con la dirección positiva del eje
numéricamente igual a la tangente del ángulo formado por la tangente en un punto dado con la dirección positiva del eje  .
.
2.3. Tabla de fórmulas básicas de diferenciación.
Función de potencia
|
|
|
|
|
|
|
Funcion exponencial
|
|
|
|
|
función logarítmica
|
|
|
|
|
Funcion trigonometrica
|
|
|
|
|
|
|
|
|
|
Función trigonométrica inversa
|
|
|
|
|
|
|
|
|
|
2.4. Reglas de diferenciación.
Derivado de 

Derivada de la suma (diferencia) de funciones


Derivada del producto de dos funciones


Derivada del cociente de dos funciones


2.5. Derivada de una función compleja.
Sea dada la función  tal que pueda representarse en la forma
tal que pueda representarse en la forma
 Y
Y  , donde la variable
, donde la variable  es un argumento intermedio, entonces
es un argumento intermedio, entonces 
La derivada de una función compleja es igual al producto de la derivada de la función dada con respecto al argumento intermedio y la derivada del argumento intermedio con respecto a x.
Ejemplo 1. 

Ejemplo 2. 

3. Función diferencial.
Dejalo ser  , diferenciable en un cierto intervalo
, diferenciable en un cierto intervalo  Déjalo ir en
esta función tiene una derivada
Déjalo ir en
esta función tiene una derivada
 ,
,
entonces podemos escribir
 (1),
(1),
Dónde  - una cantidad infinitesimal,
- una cantidad infinitesimal,
desde cuando 
Multiplicando todos los términos de igualdad (1) por  tenemos:
tenemos:
Dónde  - b.m.v. orden superior.
- b.m.v. orden superior.
Magnitud  llamado diferencial de la función
llamado diferencial de la función  y es designado
y es designado 
 .
.
3.1. Valor geométrico del diferencial.
Sea dada la función  .
.

Figura 2. Significado geométrico de diferencial.
 .
.
Obviamente, el diferencial de la función  es igual al incremento de la ordenada de la tangente en un punto dado.
es igual al incremento de la ordenada de la tangente en un punto dado.
3.2. Derivados y diferenciales de diversos órdenes.
Sí hay  , Entonces
, Entonces  se llama primera derivada.
se llama primera derivada.
La derivada de la primera derivada se llama derivada de segundo orden y se escribe  .
.
Derivada del enésimo orden de la función  se llama derivada de orden (n-1) y se escribe:
se llama derivada de orden (n-1) y se escribe:
 .
.
La diferencial de la diferencial de una función se llama diferencial de segundo o diferencial de segundo orden.
 .
.

 .
.
3.3 Resolución de problemas biológicos mediante diferenciación.
Tarea 1. Los estudios han demostrado que el crecimiento de una colonia de microorganismos obedece a la ley.  , Dónde norte
– número de microorganismos (en miles), t
– tiempo (días).
, Dónde norte
– número de microorganismos (en miles), t
– tiempo (días).
b) ¿La población de la colonia aumentará o disminuirá durante este período?
Respuesta. El tamaño de la colonia aumentará.
Tarea 2. El agua del lago se analiza periódicamente para controlar el contenido de bacterias patógenas. A través de t días después de la prueba, la concentración de bacterias está determinada por la proporción
 .
.
¿Cuándo tendrá el lago una concentración mínima de bacterias y será posible nadar en él?
Solución: Una función alcanza el máximo o el mínimo cuando su derivada es cero.
 ,
,
Determinemos que el máximo o el mínimo serán en 6 días. Para hacer esto, tomemos la segunda derivada.


Respuesta: Después de 6 días habrá una concentración mínima de bacterias.
Entonces, tenemos potencias de dos. Si tomas el número de la línea inferior, podrás encontrar fácilmente la potencia a la que tendrás que elevar dos para obtener este número. Por ejemplo, para obtener 16, debes elevar dos a la cuarta potencia. Y para obtener 64, debes elevar dos a la sexta potencia. Esto se puede ver en la tabla.
Y ahora, en realidad, la definición del logaritmo:
El logaritmo en base a de x es la potencia a la que se debe elevar a para obtener x.
Designación: log a x = b, donde a es la base, x es el argumento, b es a lo que realmente es igual el logaritmo.
Por ejemplo, 2 3 = 8 ⇒ log 2 8 = 3 (el logaritmo en base 2 de 8 es tres porque 2 3 = 8). Con el mismo éxito log 2 64 = 6, ya que 2 6 = 64.
La operación de encontrar el logaritmo de un número con una base determinada se llama logaritmización. Entonces, agreguemos una nueva línea a nuestra tabla:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| iniciar sesión 2 2 = 1 | iniciar sesión 2 4 = 2 | iniciar sesión 2 8 = 3 | iniciar sesión 2 16 = 4 | iniciar sesión 2 32 = 5 | registro 2 64 = 6 |
Desafortunadamente, no todos los logaritmos se calculan tan fácilmente. Por ejemplo, intente encontrar log 2 5. El número 5 no está en la tabla, pero la lógica dicta que el logaritmo estará en algún lugar del segmento. porque 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Estos números se llaman irracionales: los números después del punto decimal se pueden escribir hasta el infinito y nunca se repiten. Si el logaritmo resulta irracional, es mejor dejarlo así: log 2 5, log 3 8, log 5 100.
Es importante entender que un logaritmo es una expresión con dos variables (la base y el argumento). Al principio, mucha gente confunde dónde está la base y dónde está el argumento. Para evitar molestos malentendidos, basta con mirar la imagen:
Ante nosotros no hay más que la definición de logaritmo. Recordar: el logaritmo es una potencia, en el que se debe construir la base para obtener un argumento. Es la base la que está elevada a una potencia; está resaltada en rojo en la imagen. ¡Resulta que la base siempre está abajo! Les digo a mis alumnos esta maravillosa regla desde la primera lección, y no surge ninguna confusión.
Hemos descubierto la definición; solo queda aprender a contar logaritmos, es decir. deshazte del signo "registro". Para empezar, observamos que de la definición se desprenden dos hechos importantes:
- El argumento y la base siempre deben ser mayores que cero. Esto se desprende de la definición de grado mediante un exponente racional, al que se reduce la definición de logaritmo.
- La base debe ser diferente de uno, ya que uno, en cualquier grado, sigue siendo uno. Debido a esto, la pregunta “¿a qué potencia hay que elevar uno para obtener dos” no tiene sentido. ¡No existe tal grado!
Estas restricciones se denominan rango de valores aceptables(ODZ). Resulta que la ODZ del logaritmo se ve así: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Tenga en cuenta que no existen restricciones sobre el número b (el valor del logaritmo). Por ejemplo, el logaritmo bien puede ser negativo: log 2 0,5 = −1, porque 0,5 = 2-1.
Sin embargo, ahora consideraremos sólo expresiones numéricas, donde no es necesario conocer el VA del logaritmo. Los autores de los problemas ya han tenido en cuenta todas las restricciones. Pero cuando entren en juego las ecuaciones y desigualdades logarítmicas, los requisitos de la licencia de conducir serán obligatorios. Después de todo, la base y el argumento pueden contener construcciones muy sólidas que no necesariamente corresponden a las restricciones anteriores.
Ahora veamos el esquema general para calcular logaritmos. Consta de tres pasos:
- Expresa la base a y el argumento x como una potencia con la mínima base posible mayor que uno. En el camino, es mejor deshacerse de los decimales;
- Resuelva la ecuación para la variable b: x = a b ;
- El número b resultante será la respuesta.
¡Eso es todo! Si el logaritmo resulta irracional, esto ya será visible en el primer paso. El requisito de que la base sea mayor que uno es muy importante: esto reduce la probabilidad de error y simplifica enormemente los cálculos. Lo mismo ocurre con las fracciones decimales: si las conviertes inmediatamente en fracciones normales, habrá muchos menos errores.
Veamos cómo funciona este esquema usando ejemplos específicos:
Tarea. Calcula el logaritmo: log 5 25
- Imaginemos la base y el argumento como una potencia de cinco: 5 = 5 1 ; 25 = 5 2 ;
- Recibimos la respuesta: 2.
Creemos y resolvamos la ecuación:
iniciar sesión 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;
Tarea. Calcula el logaritmo:
Tarea. Calcula el logaritmo: log 4 64
- Imaginemos la base y el argumento como una potencia de dos: 4 = 2 2 ; 64 = 2 6 ;
- Creemos y resolvamos la ecuación:
iniciar sesión 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Recibimos la respuesta: 3.
Tarea. Calcula el logaritmo: log 16 1
- Imaginemos la base y el argumento como una potencia de dos: 16 = 2 4 ; 1 = 2 0 ;
- Creemos y resolvamos la ecuación:
iniciar sesión 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Recibimos la respuesta: 0.
Tarea. Calcula el logaritmo: log 7 14
- Imaginemos la base y el argumento como una potencia de siete: 7 = 7 1 ; 14 no se puede representar como una potencia de siete, ya que 7 1< 14 < 7 2 ;
- Del párrafo anterior se desprende que el logaritmo no cuenta;
- La respuesta es ningún cambio: log 7 14.
Una pequeña nota sobre el último ejemplo. ¿Cómo puedes estar seguro de que un número no es una potencia exacta de otro número? Es muy simple: simplemente factorízalo en factores primos. Si la expansión tiene al menos dos factores diferentes, el número no es una potencia exacta.
Tarea. Descubra si los números son potencias exactas: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 - grado exacto, porque sólo hay un multiplicador;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - no es una potencia exacta, ya que existen dos factores: 3 y 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - grado exacto;
35 = 7 · 5 - nuevamente no es una potencia exacta;
14 = 7 · 2 - nuevamente no es un grado exacto;
Tenga en cuenta también que los números primos en sí son siempre potencias exactas de sí mismos.
logaritmo decimal
Algunos logaritmos son tan comunes que tienen un nombre y símbolo especiales.
El logaritmo decimal de x es el logaritmo en base 10, es decir La potencia a la que se debe elevar el número 10 para obtener el número x. Designación: lg x.
Por ejemplo, registro 10 = 1; iniciar sesión 100 = 2; lg 1000 = 3-etc.
De ahora en adelante, cuando aparezca una frase como “Buscar lg 0.01” en un libro de texto, sepa que no se trata de un error tipográfico. Este es un logaritmo decimal. Sin embargo, si no estás familiarizado con esta notación, siempre puedes reescribirla:
registro x = registro 10 x
Todo lo que es cierto para los logaritmos ordinarios también lo es para los logaritmos decimales.
Logaritmo natural
Hay otro logaritmo que tiene su propia designación. En cierto modo, es incluso más importante que el decimal. Estamos hablando del logaritmo natural.
El logaritmo natural de x es el logaritmo en base e, es decir la potencia a la que se debe elevar el número e para obtener el número x. Designación: ln x .
Muchos se preguntarán: ¿cuál es el número e? Este es un número irracional; su valor exacto no se puede encontrar ni escribir. Daré sólo las primeras cifras:
mi = 2,718281828459...
No entraremos en detalles sobre qué es este número y por qué es necesario. Solo recuerda que e es la base del logaritmo natural:
ln x = log e x
Así ln e = 1 ; En mi 2 = 2; En mi 16 = 16 - etc. Por otra parte, ln 2 es un número irracional. En general, el logaritmo natural de cualquier número racional es irracional. Excepto, por supuesto, para la unidad: ln 1 = 0.
Para los logaritmos naturales, son válidas todas las reglas que son verdaderas para los logaritmos ordinarios.
- Mi cuñada es mi enemiga, ¿por qué sonic?
- Estudios ambientales
- Nuevo líder, viejo líder
- Finanzas en economía. Sistema bancario. Finanzas en economía Presentación estudios sociales Finanzas en economía de 11º grado
- Presentación sobre el tema de las finanzas en la economía.
- Origen e historia del pueblo ávar.
- Dispositivos médicos para el tratamiento de las articulaciones en el hogar Dispositivo de fisioterapia ultrasónico doméstico para el tratamiento de las articulaciones
- Precios unitarios territoriales
- Levantamiento de Kronstadt ("rebelión") (1921) Represión del levantamiento de Kronstadt
- Sistema taoísta. L. BingSecretos del amor. Práctica taoísta para mujeres y hombres. Sistema "Tao Universal"
- Qigong: práctica china para fortalecer el cuerpo
- Receta de pepinos ligeramente salados en 1 hora
- Paté de hígado de cerdo en olla de cocción lenta Paté de hígado de res en olla de cocción lenta
- Pastel de frutas de mantequilla
- Abadejo al horno
- Ensalada "Obzhorka": una receta clásica con carne de res Taraev obzhorka
- En un sueño, cambiar los pisos de la casa.
- ¿Por qué sueñas con uvas? Interpretación del sueño.
- Receta de puré de conejo para bebés
- Interpretación de los sueños: ¿por qué sueñas con Pasos? ¿Qué significa ver Pasos en un sueño?







































